1
since this page started loading...
π
Methodology, Parameters, and Calculations
Parameter definitions, formulas, uncertainty ranges, and data sources.
Keywords
health economics methodology, clinical trial cost analysis, medical research ROI, cost-benefit analysis healthcare, sensitivity analysis, Monte Carlo simulation, DALY calculation, pragmatic clinical trials
Overview
This appendix documents all 55 parameters used in the analysis, organized by type:
- External sources (peer-reviewed): 27
- Calculated values: 23
- Core definitions: 5
Calculated Values
Parameters derived from mathematical formulas and economic models.
Annual Chronic Disease Patients Treated: 982M people
Noteπ Details
Estimated unique patients receiving chronic disease treatment annually. Derived from IQVIA days of therapy (1.28T) divided by 365 days divided by 2.5 average medications per patient times 70% post-1962 drugs.
Inputs:
- Annual Days of Chronic Disease Therapy π: 1.28T days (95% CI: 1.00T days - 1.50T days)
\[ \begin{gathered} N_{treated} \\ = DOT_{chronic} \times 0.000767 \\ = 1.28T \times 0.000767 \\ = 982M \end{gathered} \]
Methodology:57
? Low confidence
Sensitivity Analysis
Sensitivity Indices for Annual Chronic Disease Patients Treated
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Global Chronic Therapy Days Annual | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
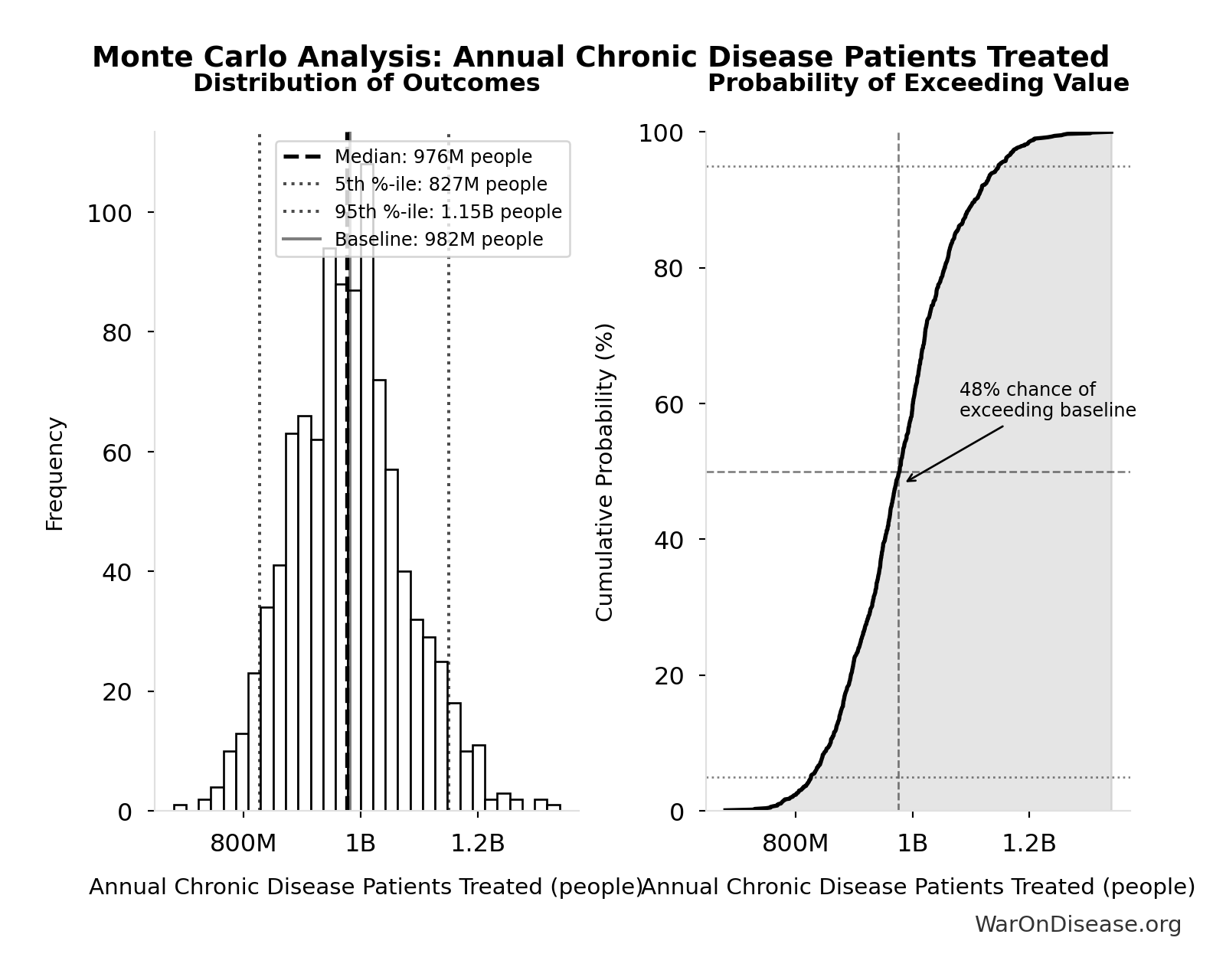
Monte Carlo Distribution
Simulation Results Summary: Annual Chronic Disease Patients Treated
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 982M |
| Mean (expected value) | 981M |
| Median (50th percentile) | 976M |
| Standard Deviation | 98.4M |
| 90% Confidence Interval | [827M, 1.15B] |
The histogram shows the distribution of Annual Chronic Disease Patients Treated across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
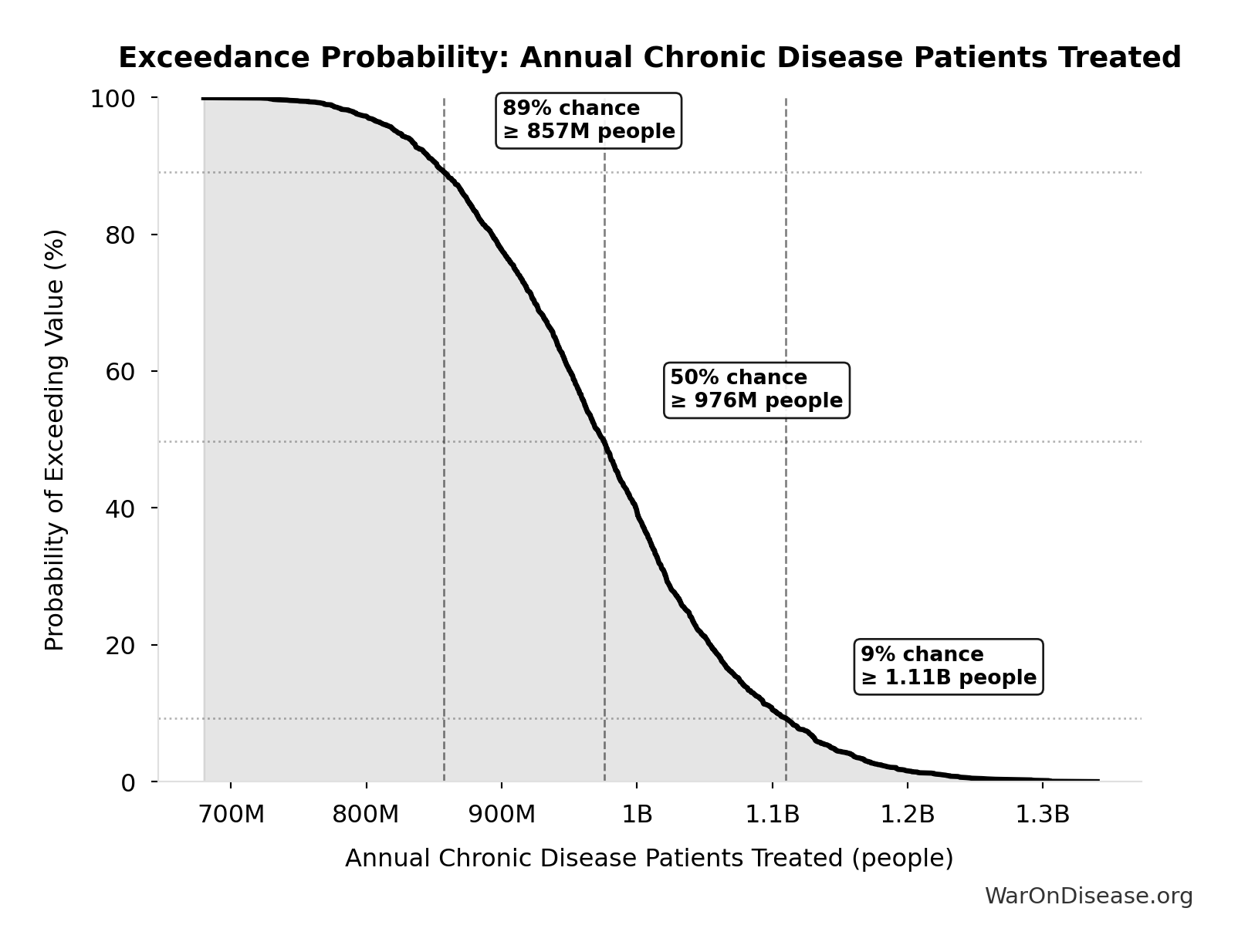
Exceedance Probability
This exceedance probability chart shows the likelihood that Annual Chronic Disease Patients Treated will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
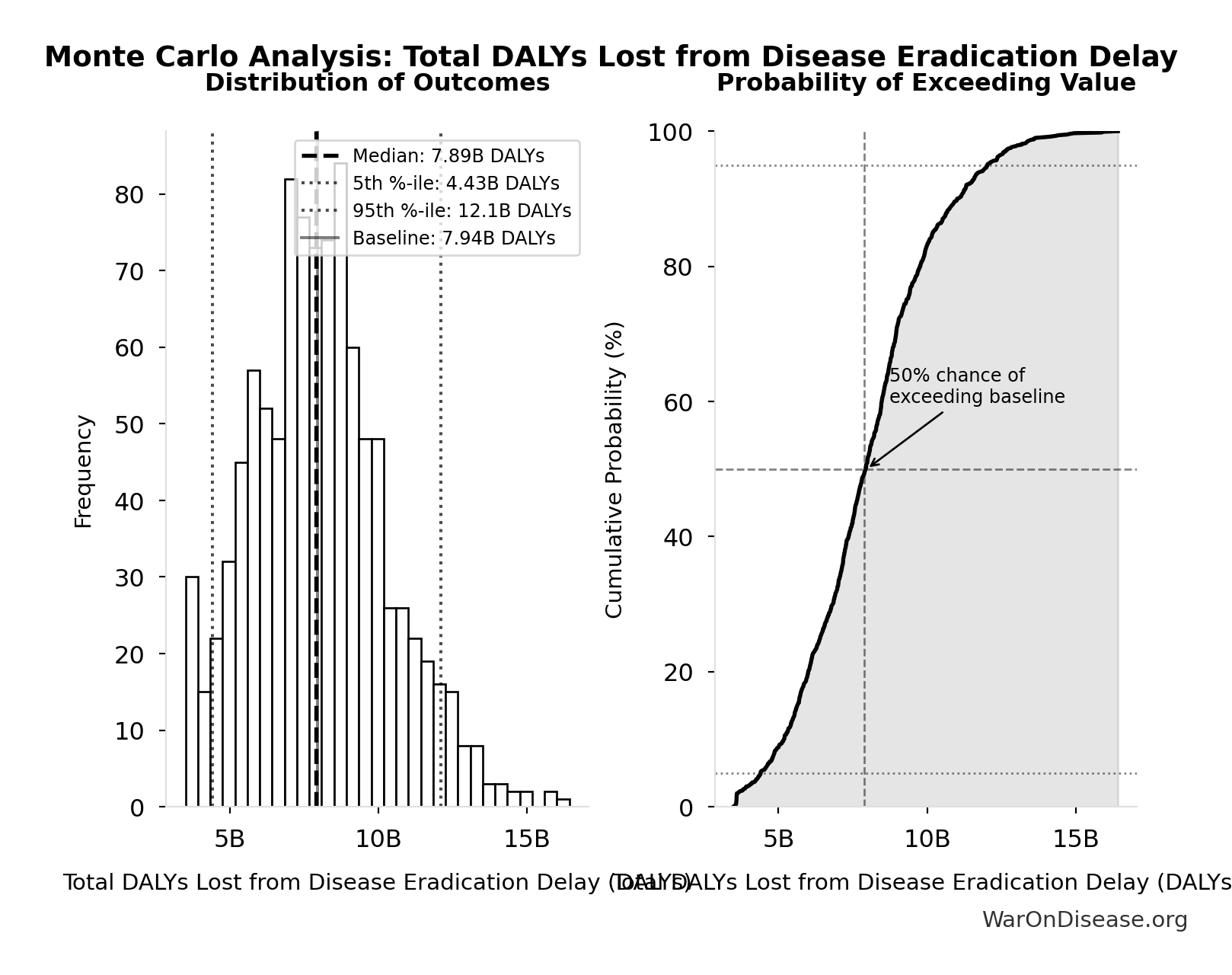
Total DALYs Lost from Disease Eradication Delay: 7.94B DALYs
Noteπ Details
Total Disability-Adjusted Life Years lost from disease eradication delay (PRIMARY estimate)
Inputs:
- Years of Life Lost from Disease Eradication Delay π’: 7.07B years
- Years Lived with Disability During Disease Eradication Delay π’: 873M years
\[ \begin{gathered} DALYs_{lag} = YLL_{lag} + YLD_{lag} = 7.07B + 873M = 7.94B \\[0.5em] \text{where } YLL_{lag} \\ = Deaths_{lag} \times (LE_{global} - Age_{death,delay}) \\ = 416M \times (79 - 62) \\ = 7.07B \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \\[0.5em] \text{where } YLD_{lag} \\ = Deaths_{lag} \times T_{suffering} \times DW_{chronic} \\ = 416M \times 6 \times 0.35 \\ = 873M \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#daly-calculation
~ Medium confidence
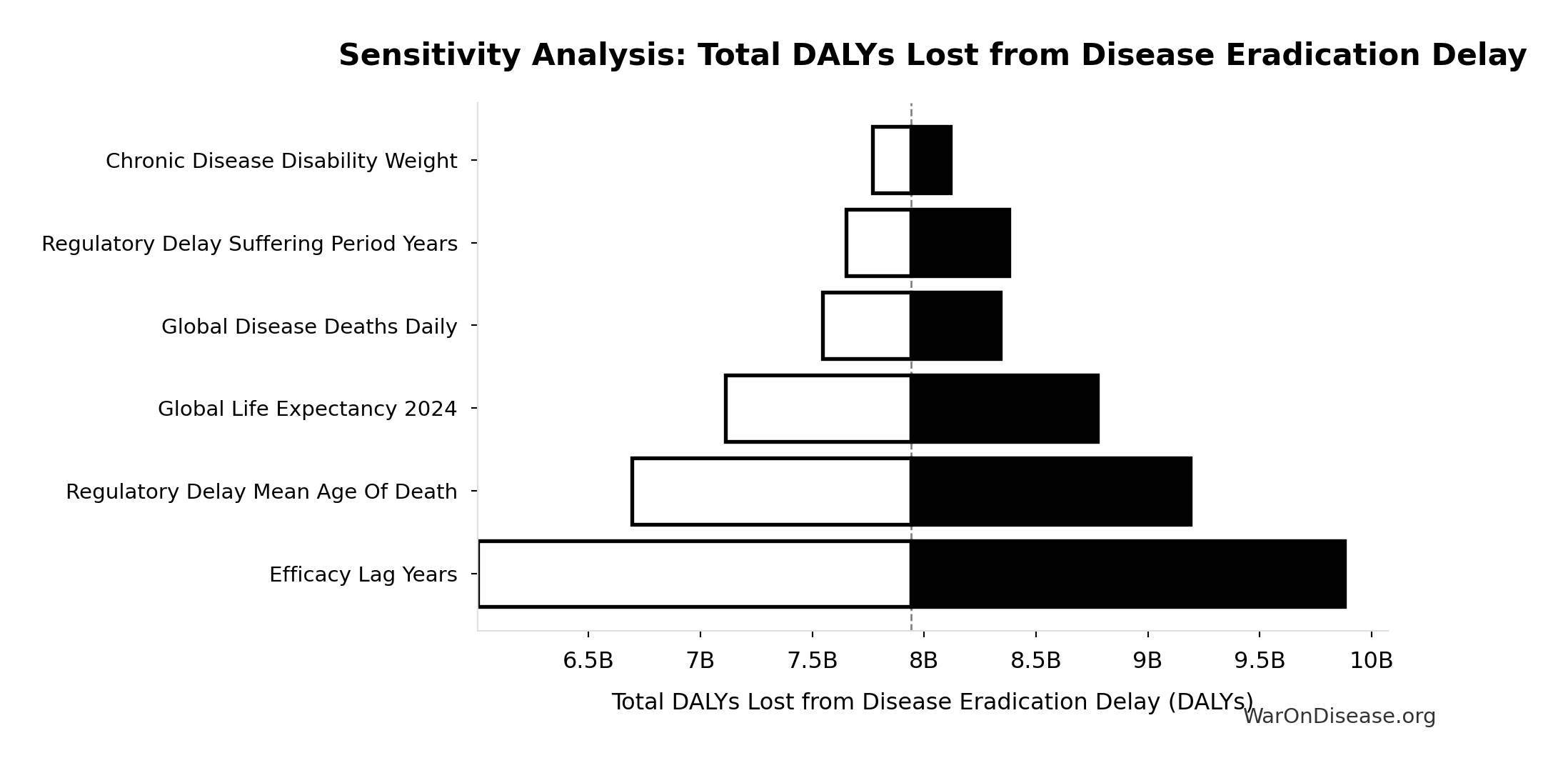
Sensitivity Analysis
Sensitivity Indices for Total DALYs Lost from Disease Eradication Delay
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| dFDA Efficacy Lag Elimination Yll | 0.7043 | Strong driver |
| dFDA Efficacy Lag Elimination Yld | 0.3107 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Total DALYs Lost from Disease Eradication Delay
| Statistic | Value |
|---|---|
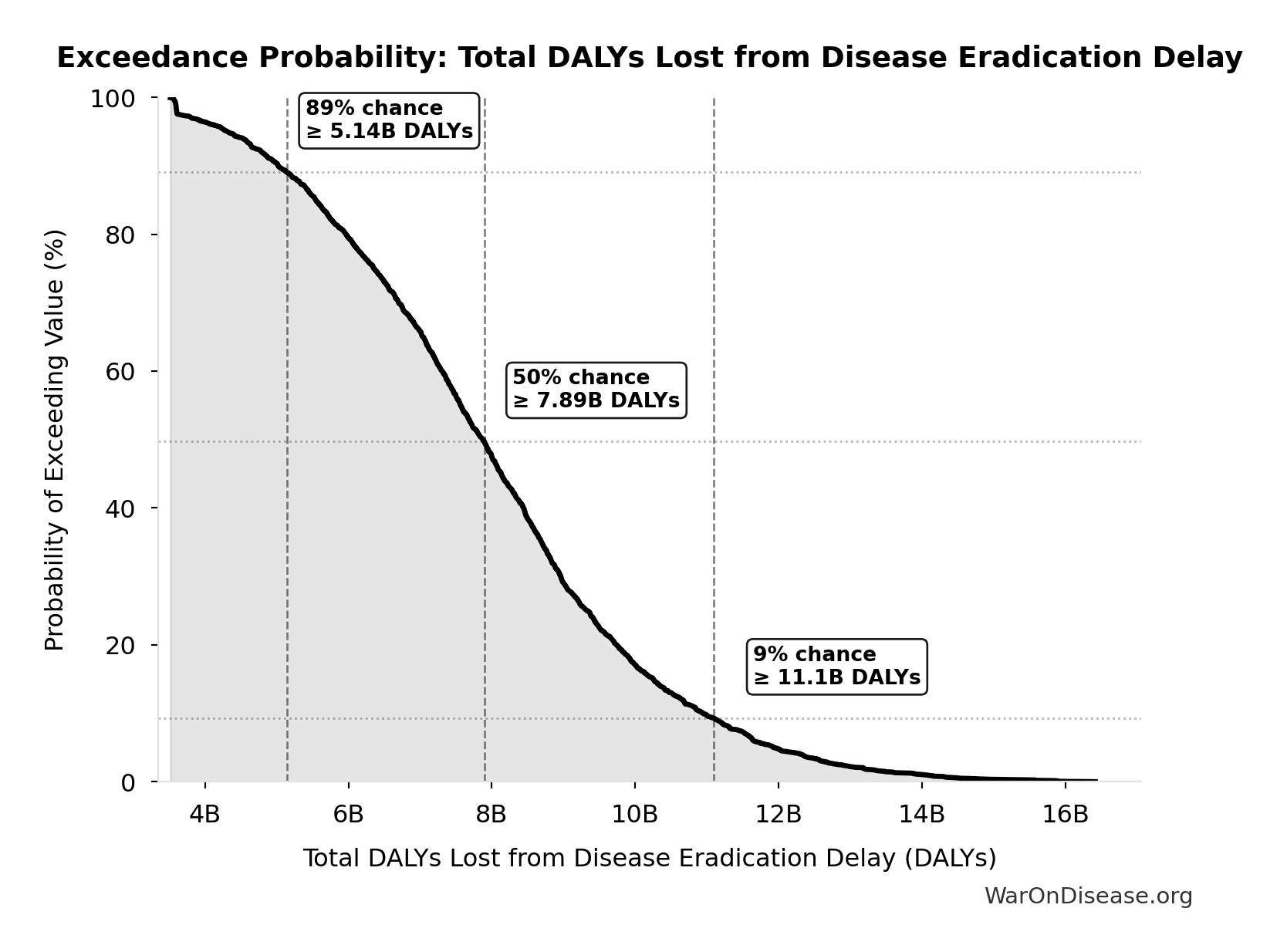
| Baseline (deterministic) | 7.94B |
| Mean (expected value) | 8.05B |
| Median (50th percentile) | 7.89B |
| Standard Deviation | 2.31B |
| 90% Confidence Interval | [4.43B, 12.1B] |
The histogram shows the distribution of Total DALYs Lost from Disease Eradication Delay across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Total DALYs Lost from Disease Eradication Delay will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
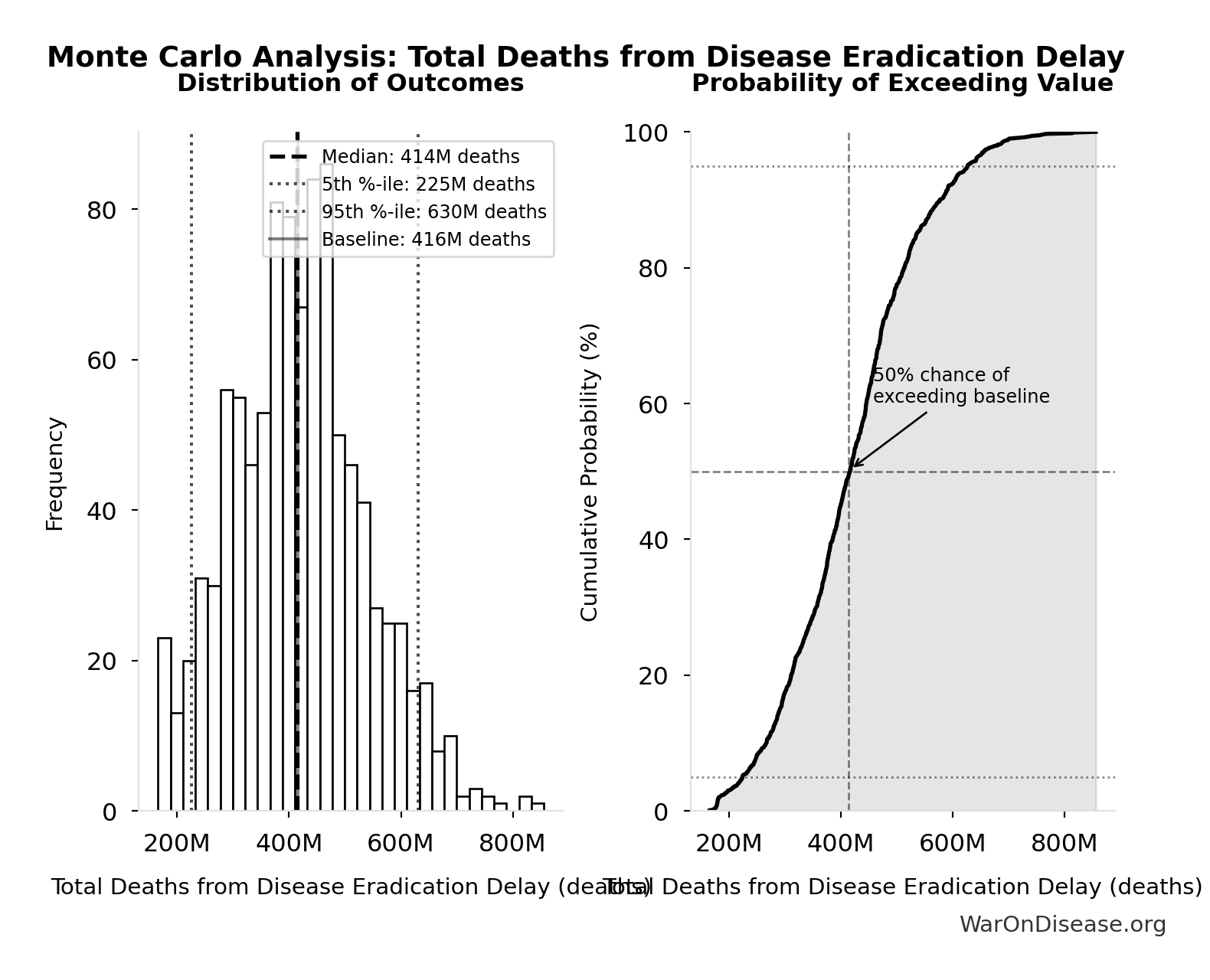
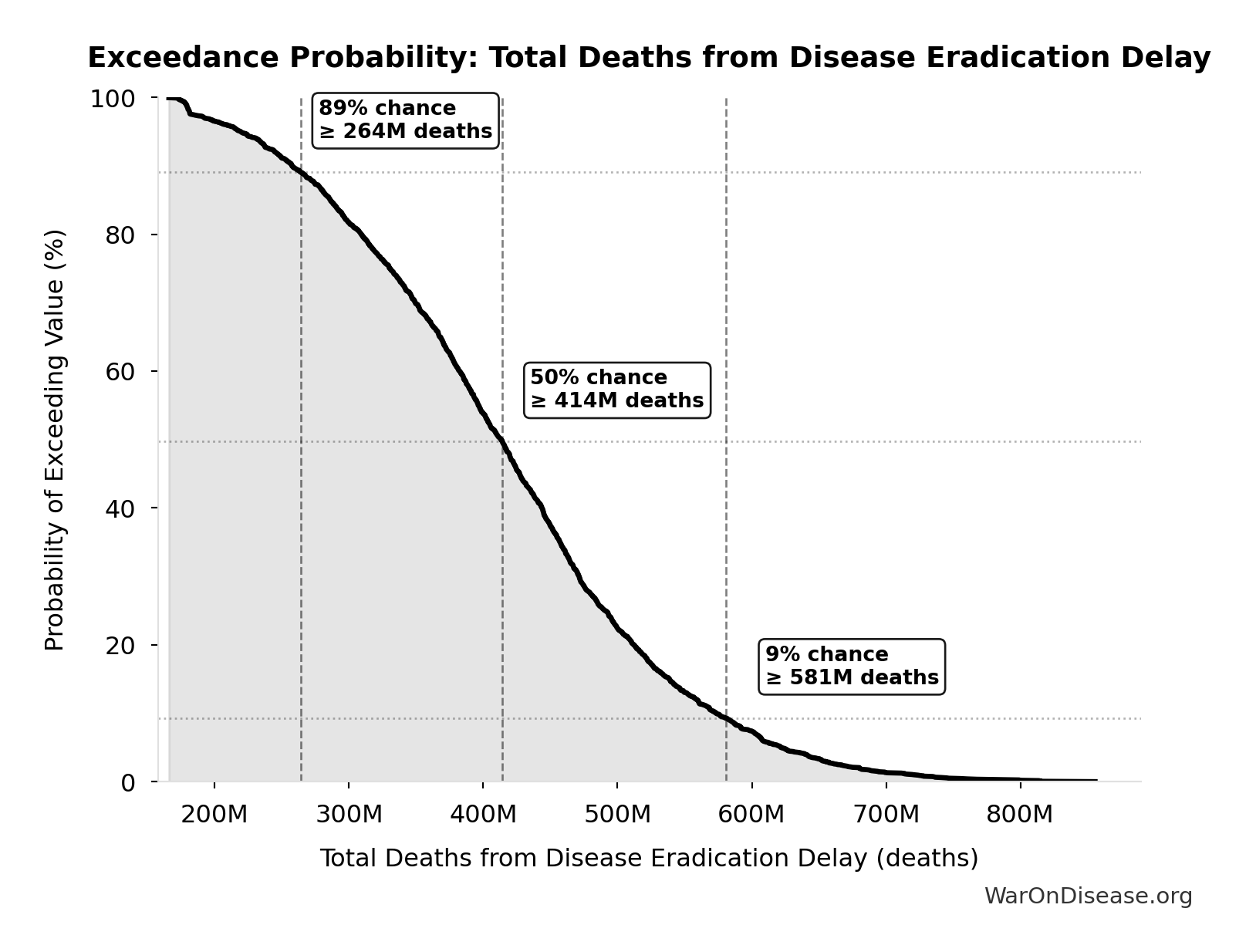
Total Deaths from Disease Eradication Delay: 416M deaths
Noteπ Details
Total eventually avoidable deaths from delaying disease eradication by 8.2 years (PRIMARY estimate, conservative). Excludes fundamentally unavoidable deaths (primarily accidents ~7.9%).
Inputs:
- Regulatory Delay for Efficacy Testing Post-Safety Verification π: 8.2 years (SE: Β±2 years)
- Global Daily Deaths from Disease and Aging π: 150k deaths/day (SE: Β±7.50k deaths/day)
\[ \begin{gathered} Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#disease-eradication-delay
~ Medium confidence
Sensitivity Analysis
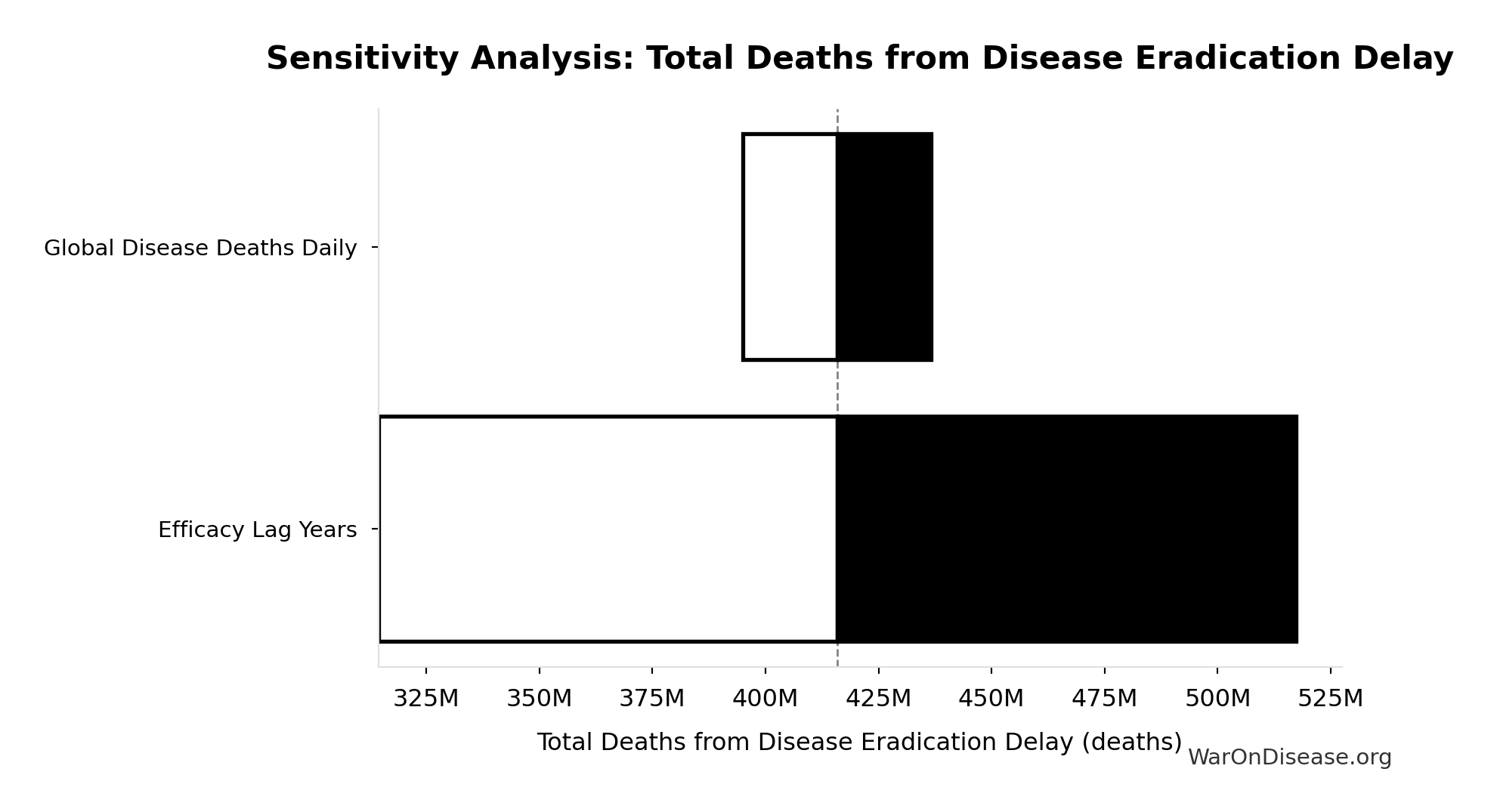
Sensitivity Indices for Total Deaths from Disease Eradication Delay
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Efficacy Lag Years | 1.1404 | Strong driver |
| Global Disease Deaths Daily | -0.1422 | Weak driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Total Deaths from Disease Eradication Delay
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 416M |
| Mean (expected value) | 420M |
| Median (50th percentile) | 414M |
| Standard Deviation | 122M |
| 90% Confidence Interval | [225M, 630M] |
The histogram shows the distribution of Total Deaths from Disease Eradication Delay across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Total Deaths from Disease Eradication Delay will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
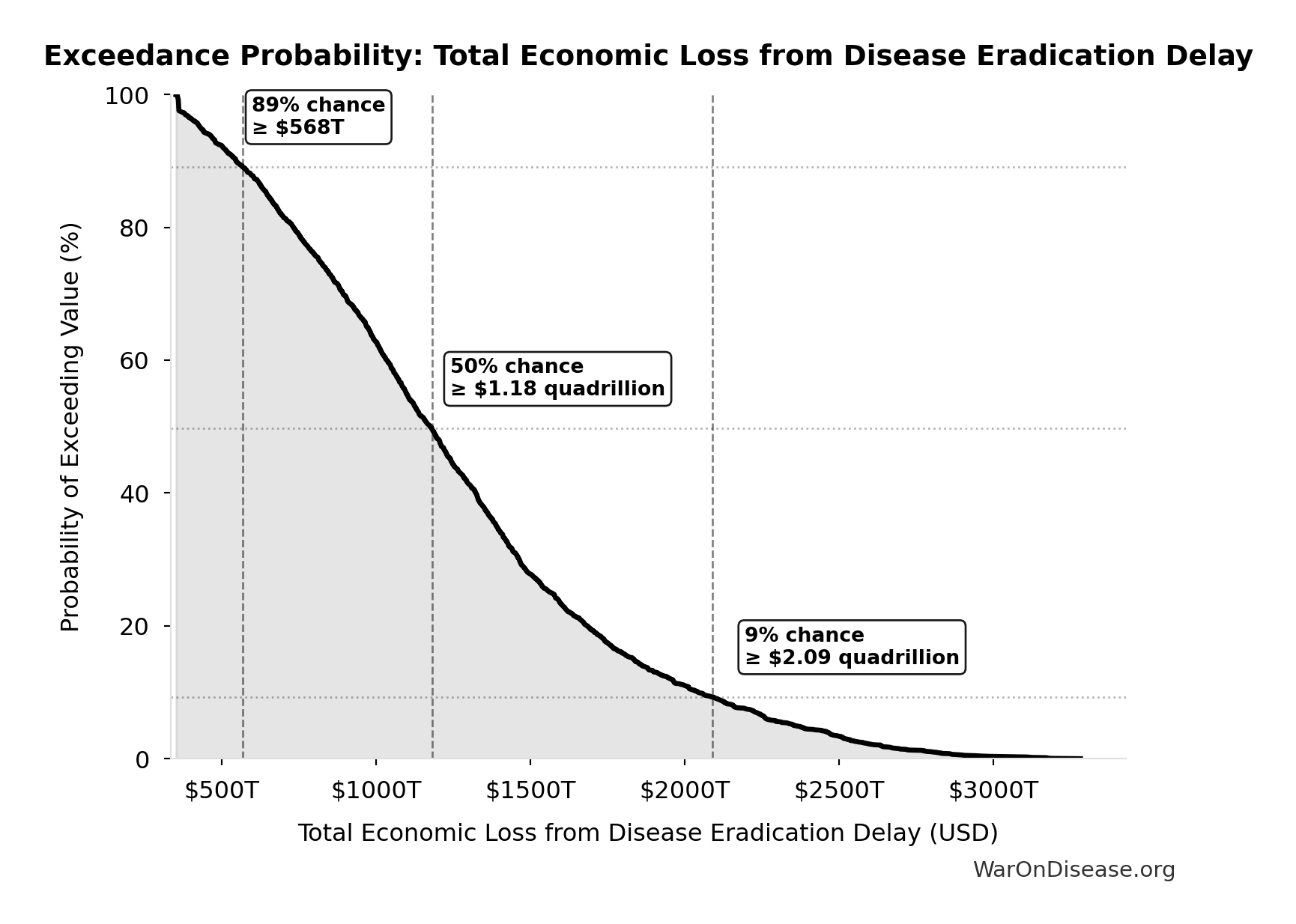
Total Economic Loss from Disease Eradication Delay: $1.19 quadrillion
Noteπ Details
Total economic loss from delaying disease eradication by 8.2 years (PRIMARY estimate, 2024 USD). Values global DALYs at standardized US/International normative rate ($150k) rather than local ability-to-pay, representing the full human capital loss.
Inputs:
- Total DALYs Lost from Disease Eradication Delay π’: 7.94B DALYs
- Standard Economic Value per QALY π: $150K (SE: Β±$30K)
\[ \begin{gathered} Value_{lag} \\ = DALYs_{lag} \times Value_{QALY} \\ = 7.94B \times \$150K \\ = \$1190T \\[0.5em] \text{where } DALYs_{lag} = YLL_{lag} + YLD_{lag} = 7.07B + 873M = 7.94B \\[0.5em] \text{where } YLL_{lag} \\ = Deaths_{lag} \times (LE_{global} - Age_{death,delay}) \\ = 416M \times (79 - 62) \\ = 7.07B \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \\[0.5em] \text{where } YLD_{lag} \\ = Deaths_{lag} \times T_{suffering} \times DW_{chronic} \\ = 416M \times 6 \times 0.35 \\ = 873M \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#economic-valuation
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Total Economic Loss from Disease Eradication Delay
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| dFDA Efficacy Lag Elimination DALYs | 1.0671 | Strong driver |
| Standard Economic QALY Value Usd | -0.0733 | Minimal effect |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
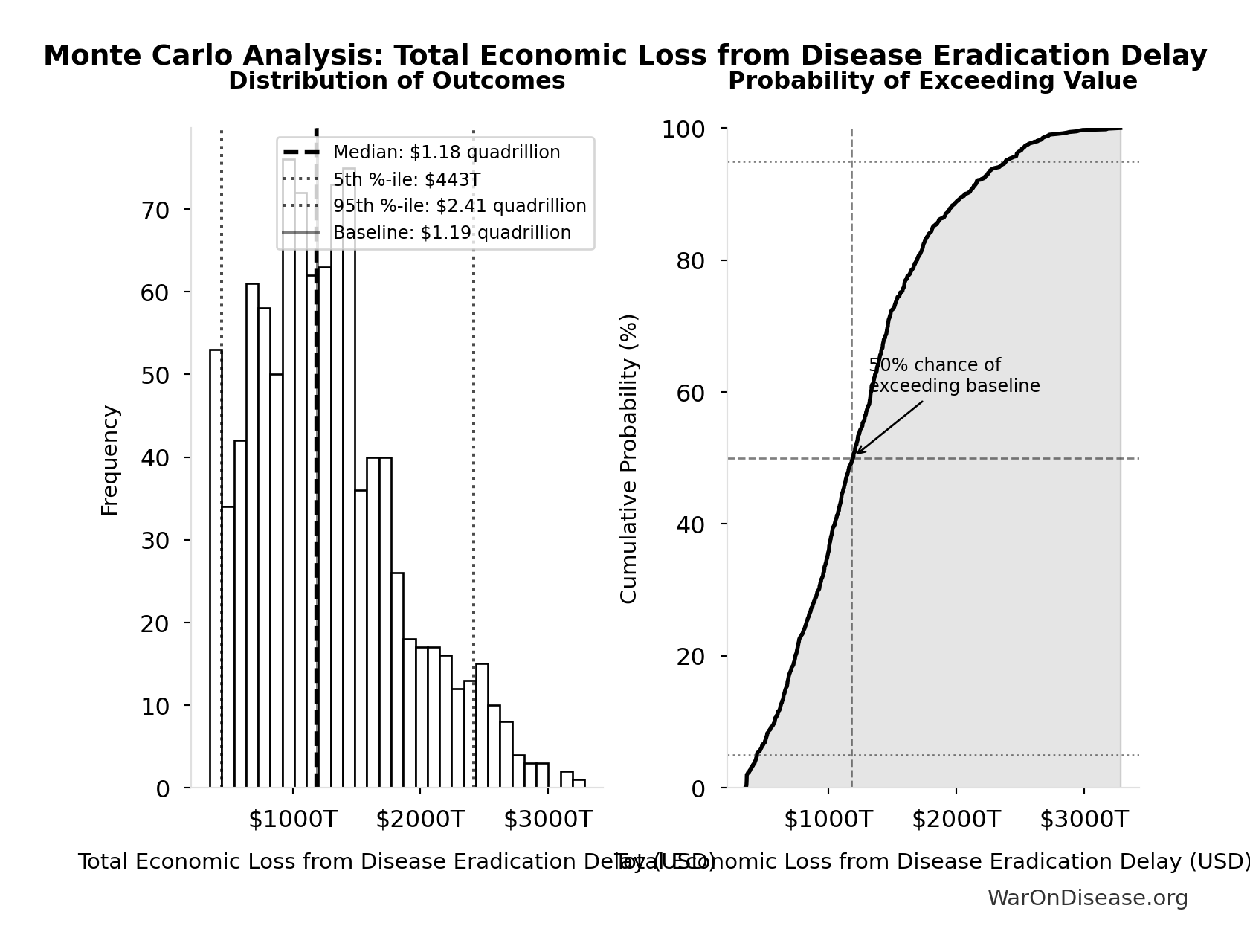
Monte Carlo Distribution
Simulation Results Summary: Total Economic Loss from Disease Eradication Delay
| Statistic | Value |
|---|---|
| Baseline (deterministic) | $1.19 quadrillion |
| Mean (expected value) | $1.27 quadrillion |
| Median (50th percentile) | $1.18 quadrillion |
| Standard Deviation | $581T |
| 90% Confidence Interval | [$443T, $2.41 quadrillion] |
The histogram shows the distribution of Total Economic Loss from Disease Eradication Delay across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Total Economic Loss from Disease Eradication Delay will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
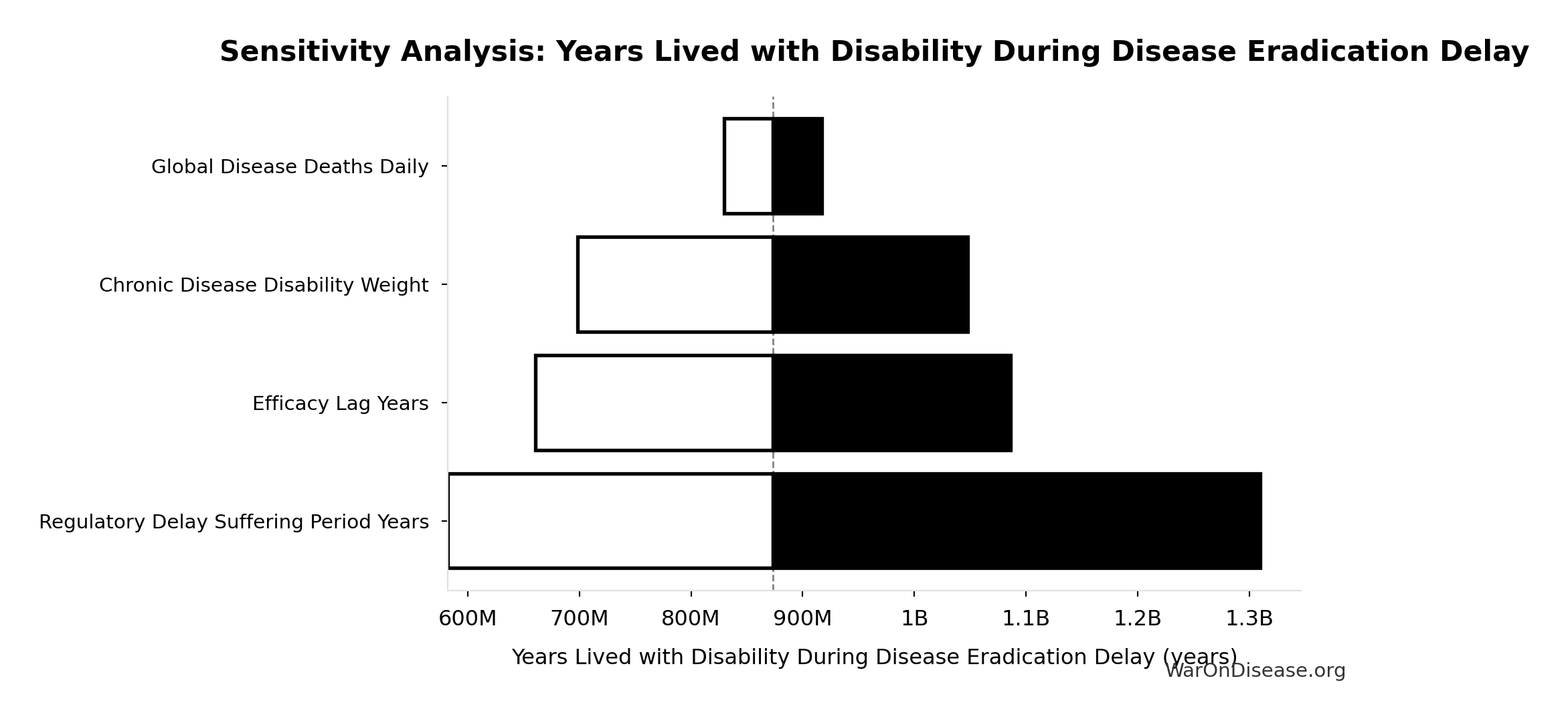
Years Lived with Disability During Disease Eradication Delay: 873M years
Noteπ Details
Years Lived with Disability during disease eradication delay (PRIMARY estimate)
Inputs:
- Total Deaths from Disease Eradication Delay π’: 416M deaths
- Pre-Death Suffering Period During Post-Safety Efficacy Delay π: 6 years (95% CI: 4 years - 9 years)
- Disability Weight for Untreated Chronic Conditions π: 0.35 weight (SE: Β±0.07 weight)
\[ \begin{gathered} YLD_{lag} \\ = Deaths_{lag} \times T_{suffering} \times DW_{chronic} \\ = 416M \times 6 \times 0.35 \\ = 873M \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#daly-calculation
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Years Lived with Disability During Disease Eradication Delay
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Regulatory Delay Suffering Period Years | 2.0883 | Strong driver |
| Chronic Disease Disability Weight | -0.9003 | Strong driver |
| dFDA Efficacy Lag Elimination Deaths Averted | -0.2255 | Weak driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
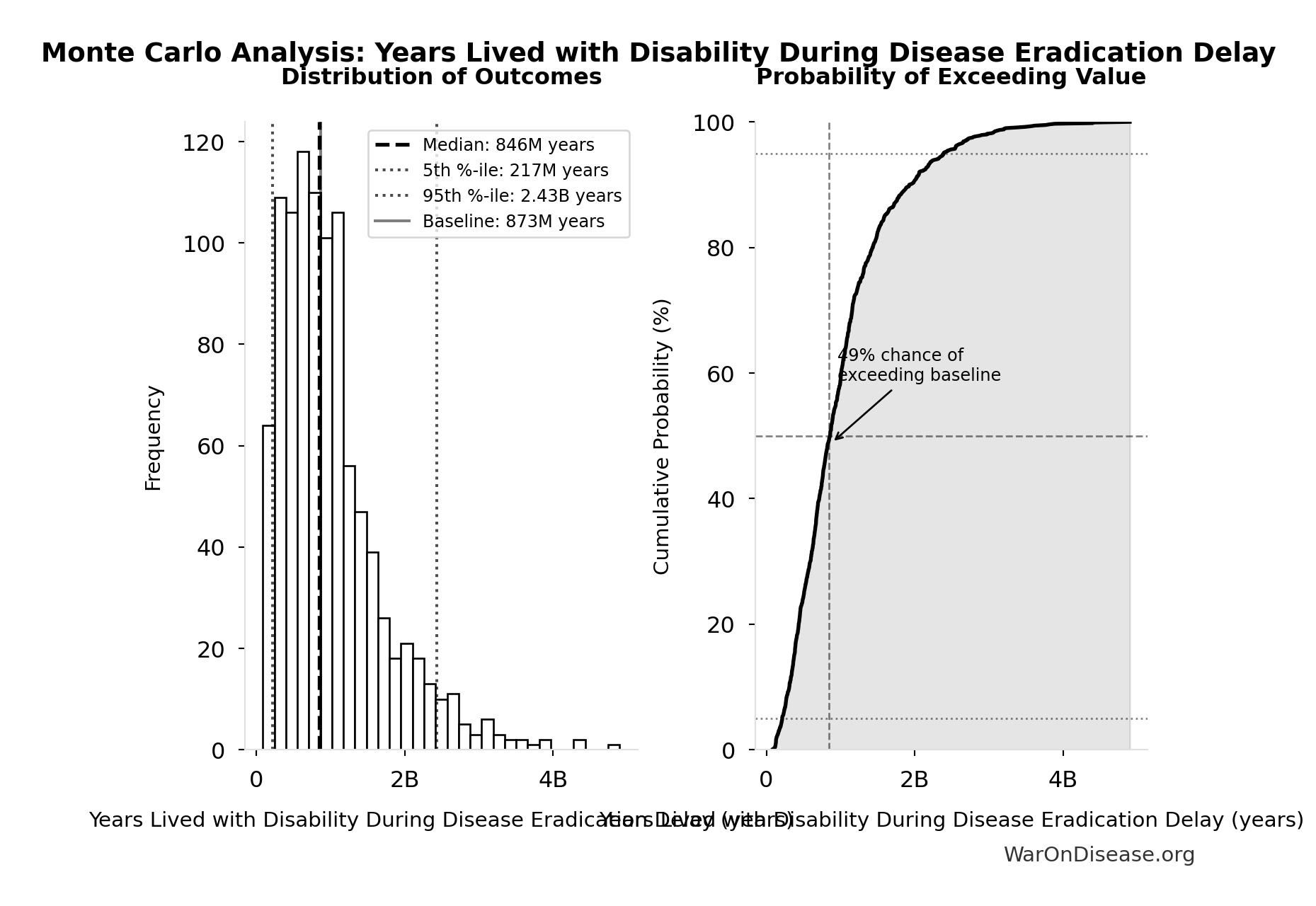
Monte Carlo Distribution
Simulation Results Summary: Years Lived with Disability During Disease Eradication Delay
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 873M |
| Mean (expected value) | 1.02B |
| Median (50th percentile) | 846M |
| Standard Deviation | 716M |
| 90% Confidence Interval | [217M, 2.43B] |
The histogram shows the distribution of Years Lived with Disability During Disease Eradication Delay across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
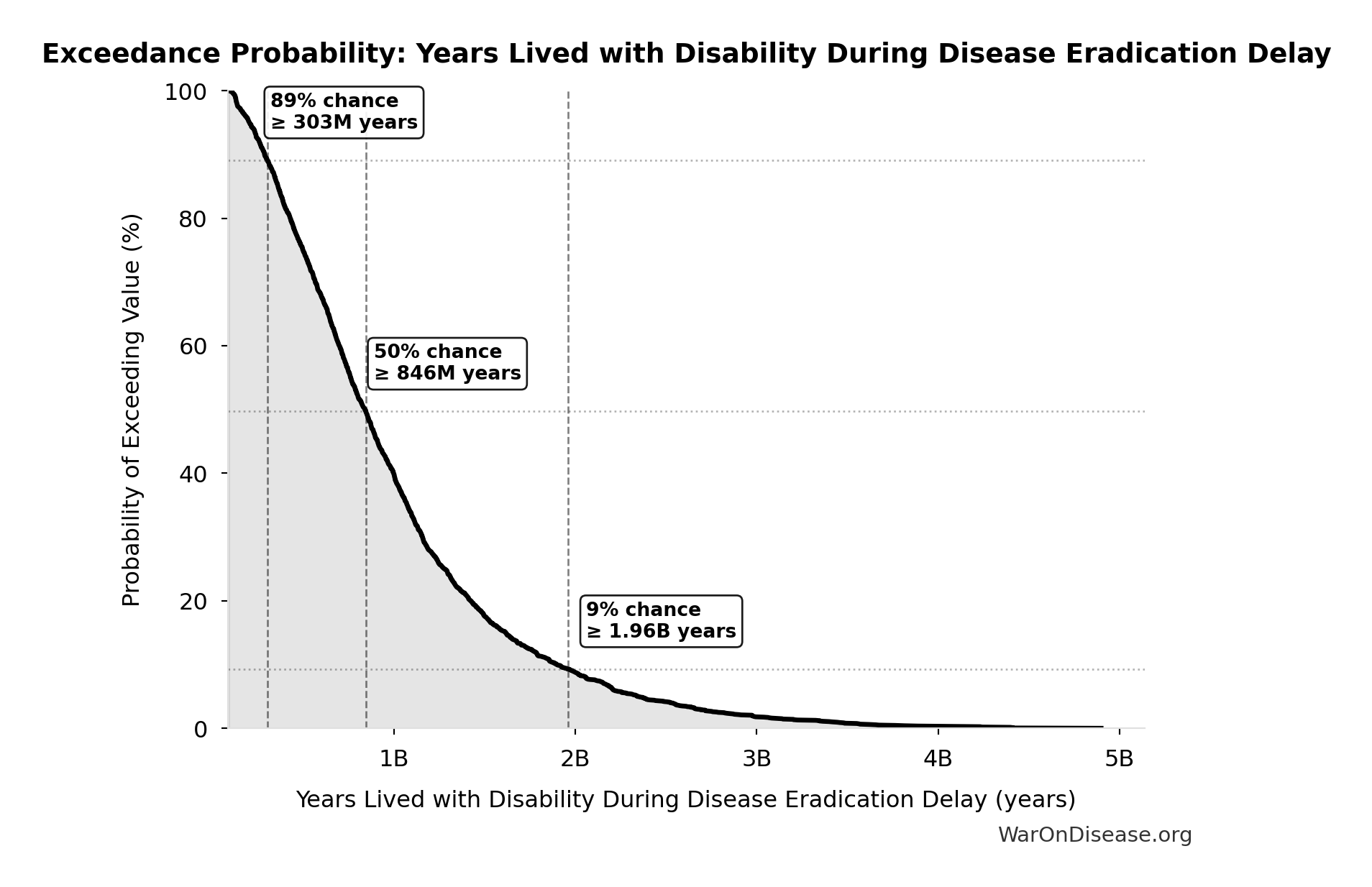
Exceedance Probability
This exceedance probability chart shows the likelihood that Years Lived with Disability During Disease Eradication Delay will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
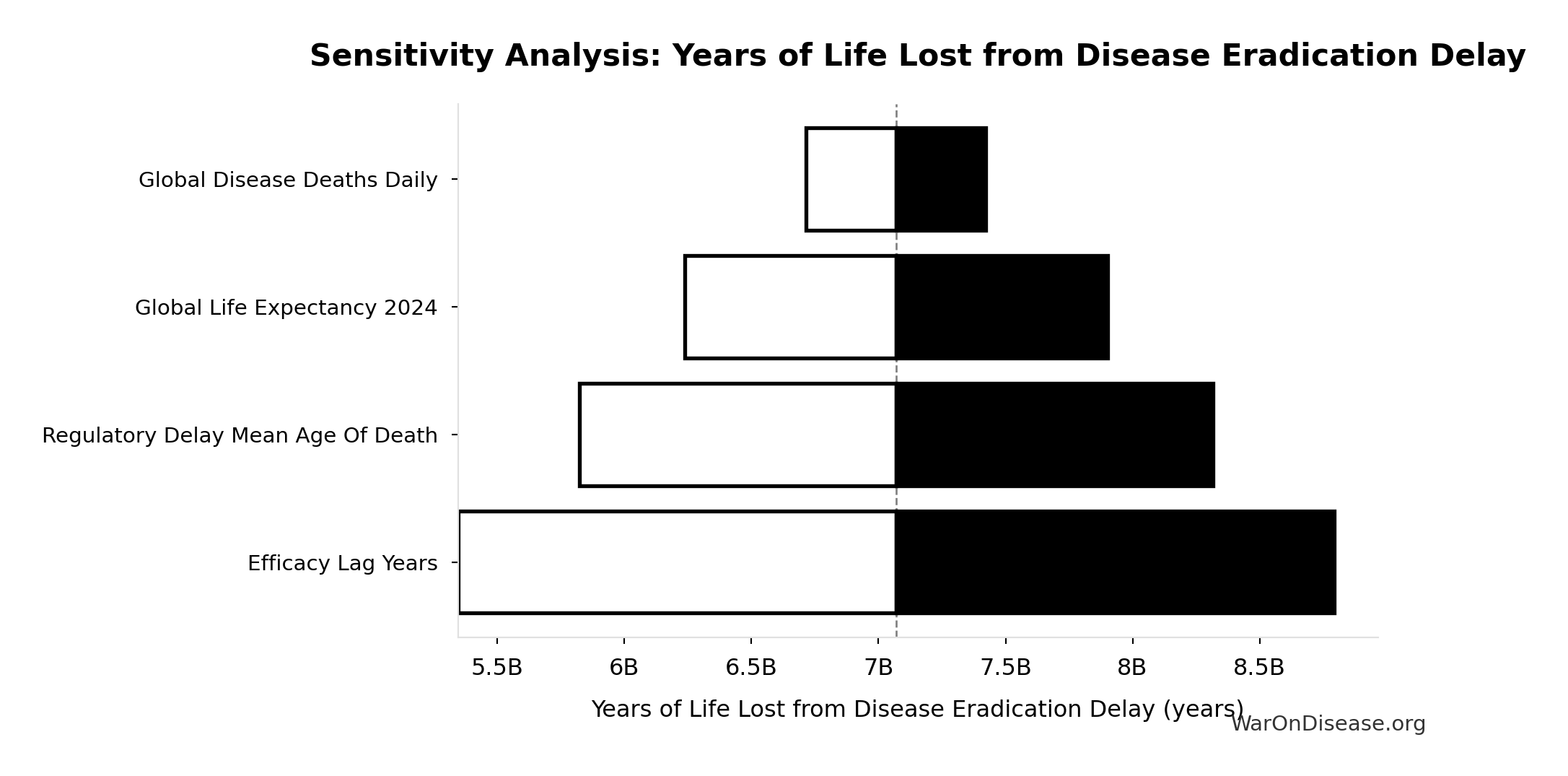
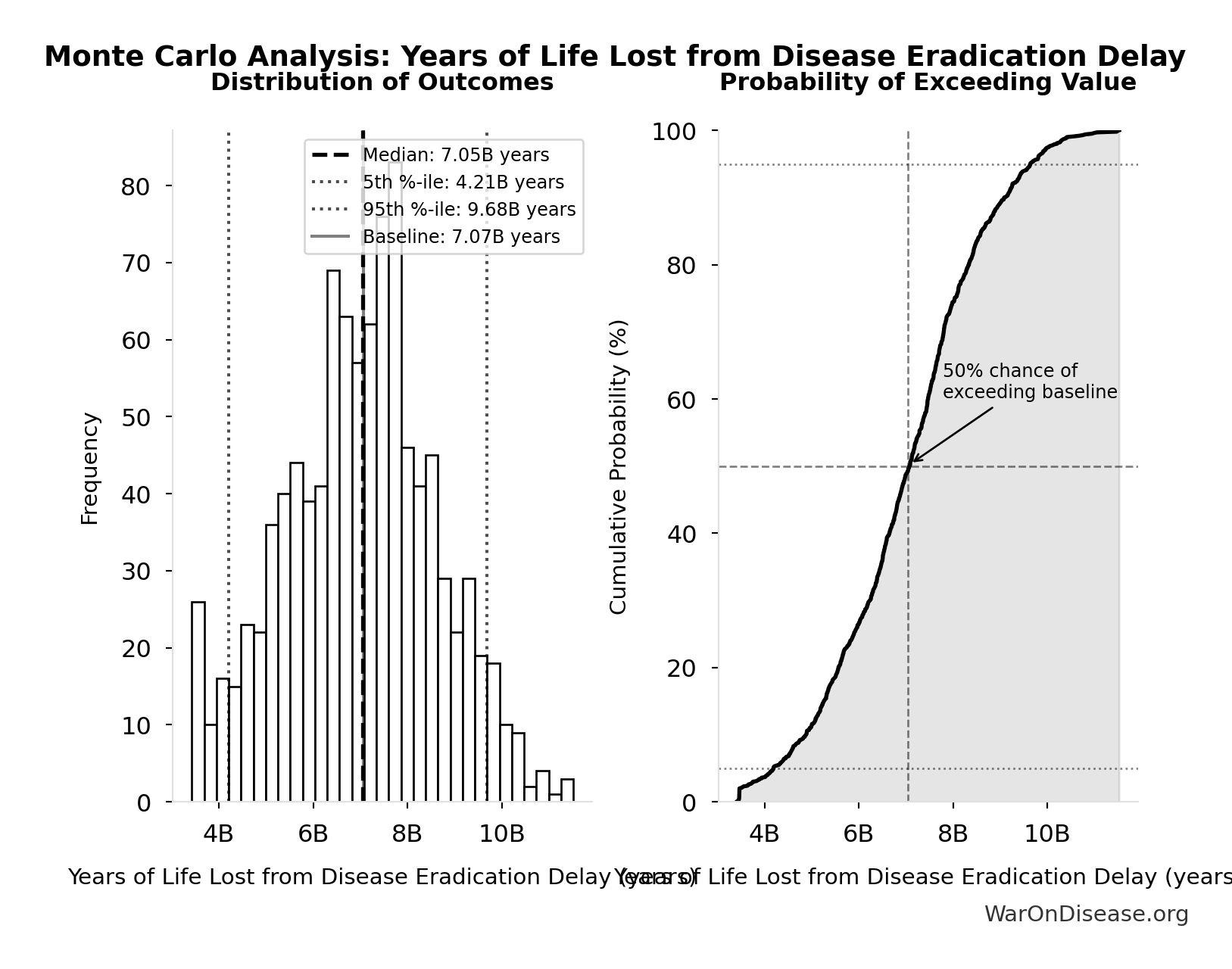
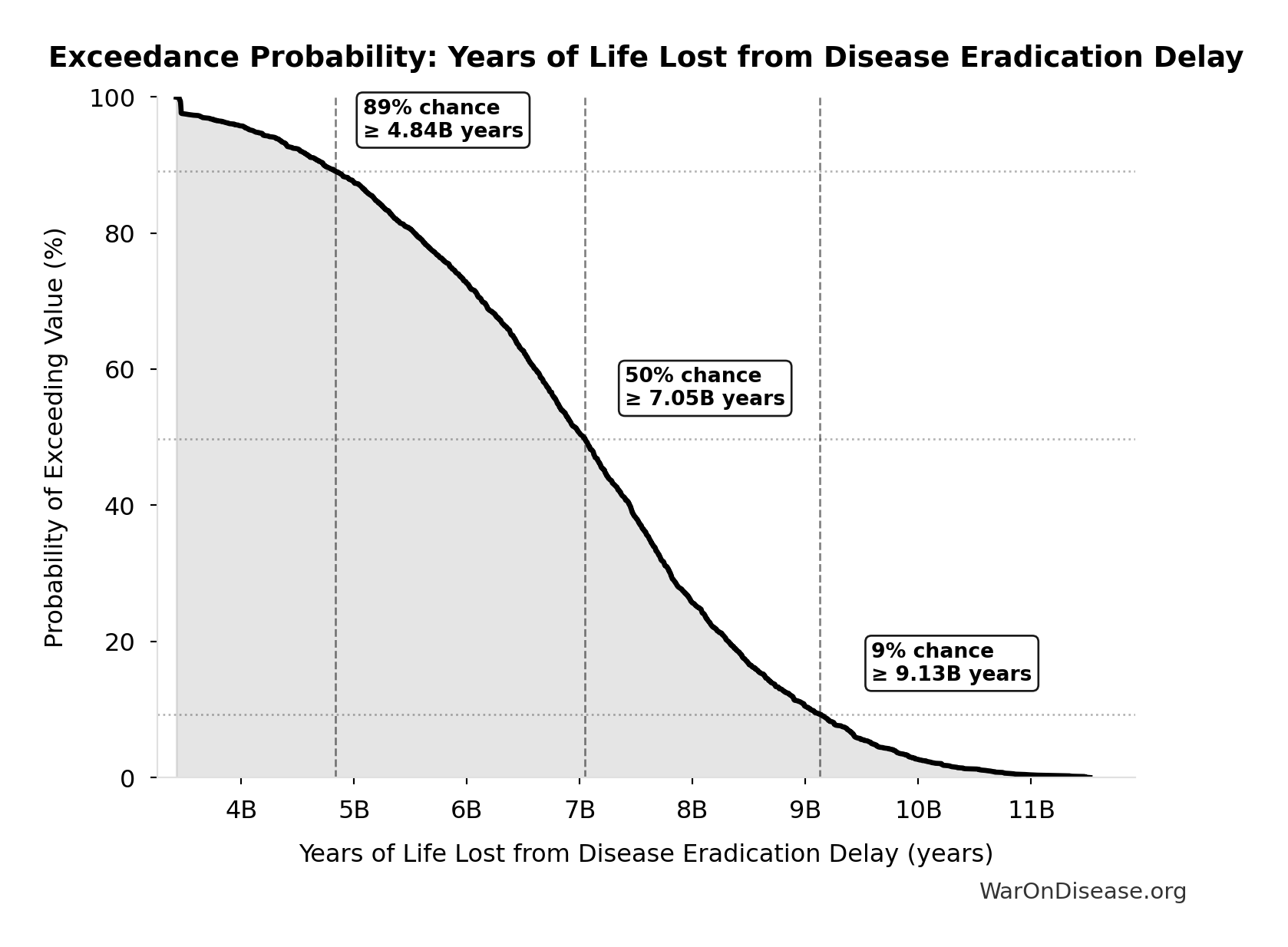
Years of Life Lost from Disease Eradication Delay: 7.07B years
Noteπ Details
Years of Life Lost from disease eradication delay deaths (PRIMARY estimate)
Inputs:
- Total Deaths from Disease Eradication Delay π’: 416M deaths
- Global Life Expectancy (2024) π: 79 years (SE: Β±2 years)
- Mean Age of Preventable Death from Post-Safety Efficacy Delay π: 62 years (SE: Β±3 years)
\[ \begin{gathered} YLL_{lag} \\ = Deaths_{lag} \times (LE_{global} - Age_{death,delay}) \\ = 416M \times (79 - 62) \\ = 7.07B \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#daly-calculation
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Years of Life Lost from Disease Eradication Delay
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Global Life Expectancy 2024 | 2.0066 | Strong driver |
| Regulatory Delay Mean Age Of Death | -1.3852 | Strong driver |
| dFDA Efficacy Lag Elimination Deaths Averted | 0.3779 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Years of Life Lost from Disease Eradication Delay
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 7.07B |
| Mean (expected value) | 7.03B |
| Median (50th percentile) | 7.05B |
| Standard Deviation | 1.62B |
| 90% Confidence Interval | [4.21B, 9.68B] |
The histogram shows the distribution of Years of Life Lost from Disease Eradication Delay across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Years of Life Lost from Disease Eradication Delay will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
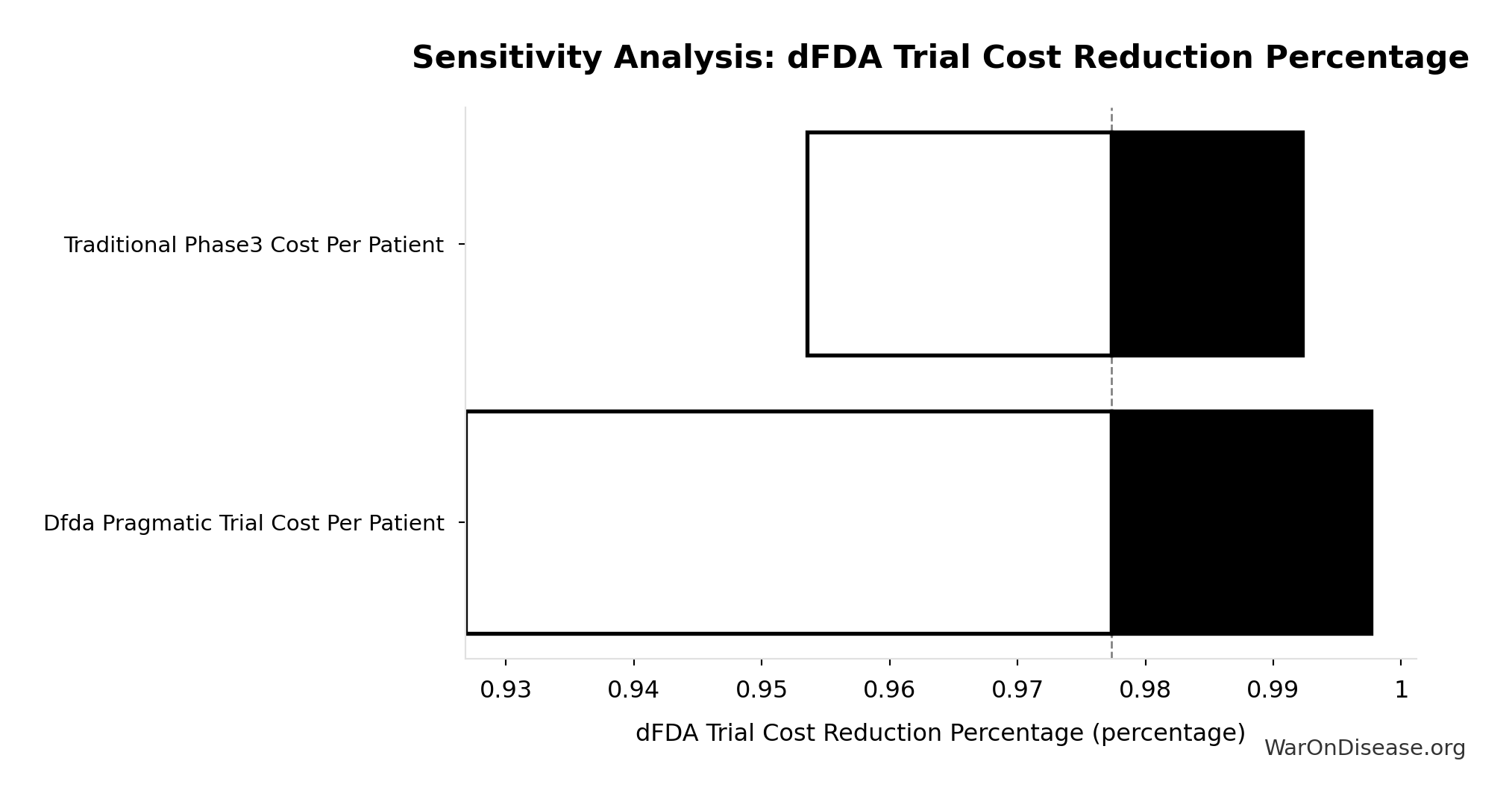
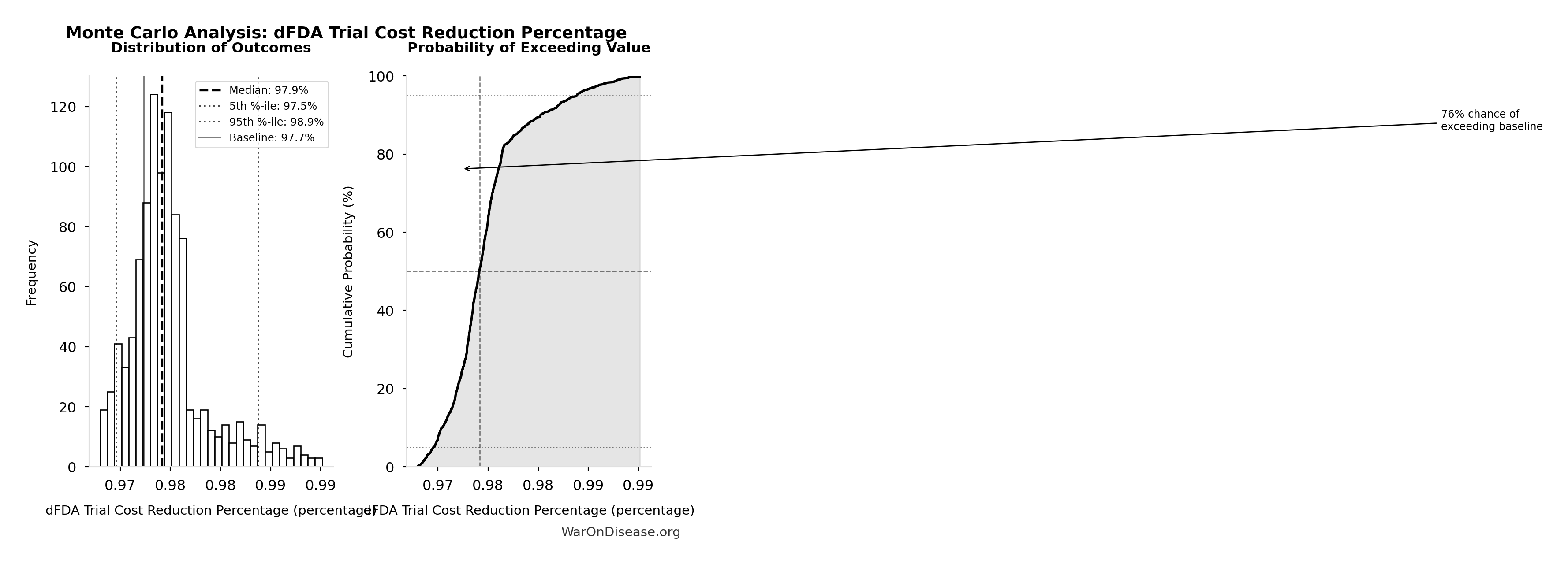
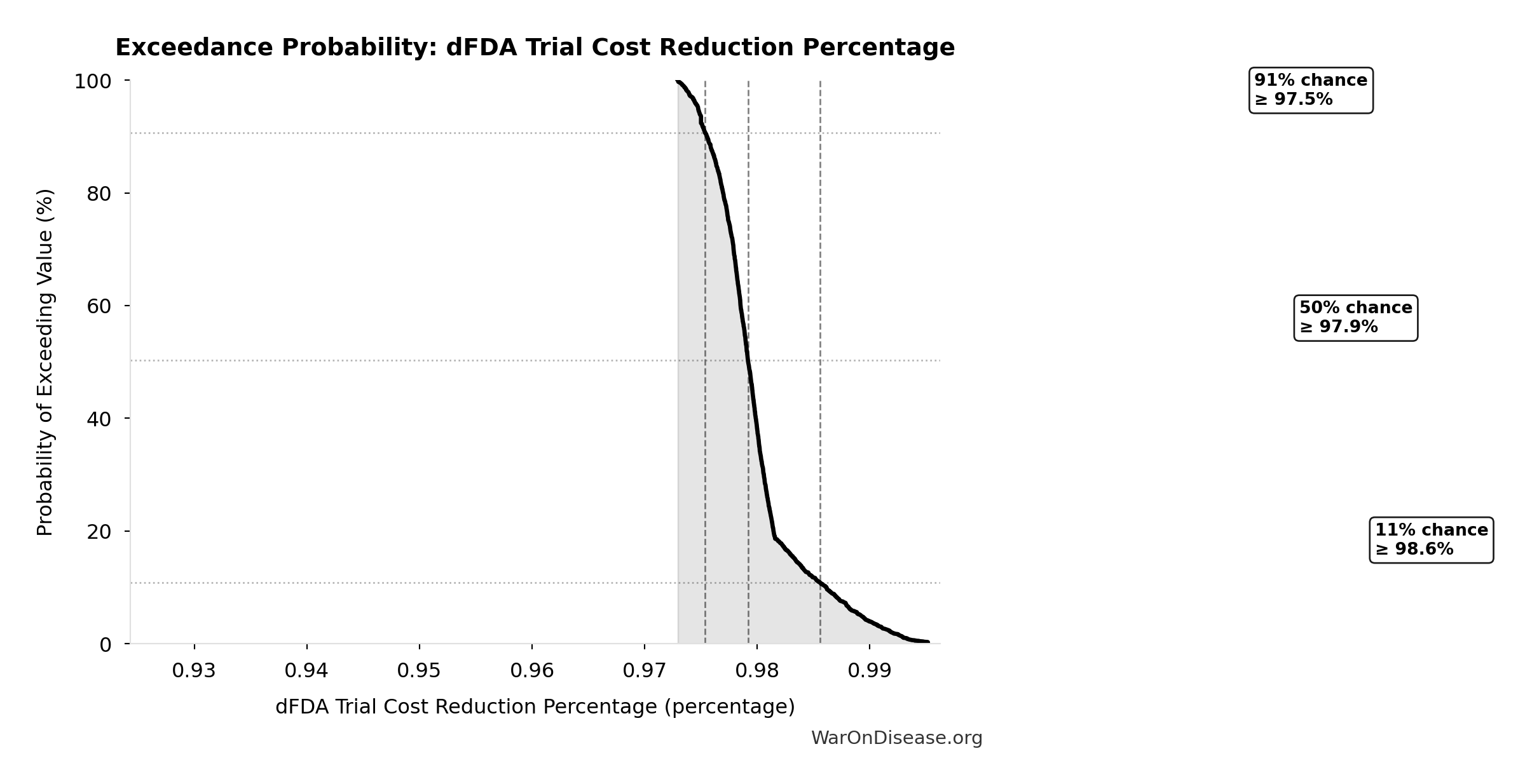
dFDA Trial Cost Reduction Percentage: 97.7%
Noteπ Details
Trial cost reduction percentage: (traditional - dFDA) / traditional = ($41K - $1.2K) / $41K = 97%
Inputs:
- dFDA Pragmatic Trial Cost per Patient π: $929 (95% CI: $97 - $3K)
- Phase 3 Cost per Patient π: $41K (95% CI: $20K - $120K)
\[ \begin{gathered} Reduce_{pct} \\ = 1 - \frac{Cost_{pragmatic,pt}}{Cost_{P3,pt}} \\ = 1 - \frac{\$929}{\$41K} \\ = 97.7\% \end{gathered} \]
Methodology: ../appendix/dfda-impact-paper#cost-reduction
β High confidence
Sensitivity Analysis
Sensitivity Indices for dFDA Trial Cost Reduction Percentage
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| dFDA Pragmatic Trial Cost Per Patient | -6.4207 | Strong driver |
| Traditional Phase3 Cost Per Patient | 5.6539 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: dFDA Trial Cost Reduction Percentage
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 97.7% |
| Mean (expected value) | 98% |
| Median (50th percentile) | 97.9% |
| Standard Deviation | 0.401% |
| 90% Confidence Interval | [97.5%, 98.9%] |
The histogram shows the distribution of dFDA Trial Cost Reduction Percentage across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that dFDA Trial Cost Reduction Percentage will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
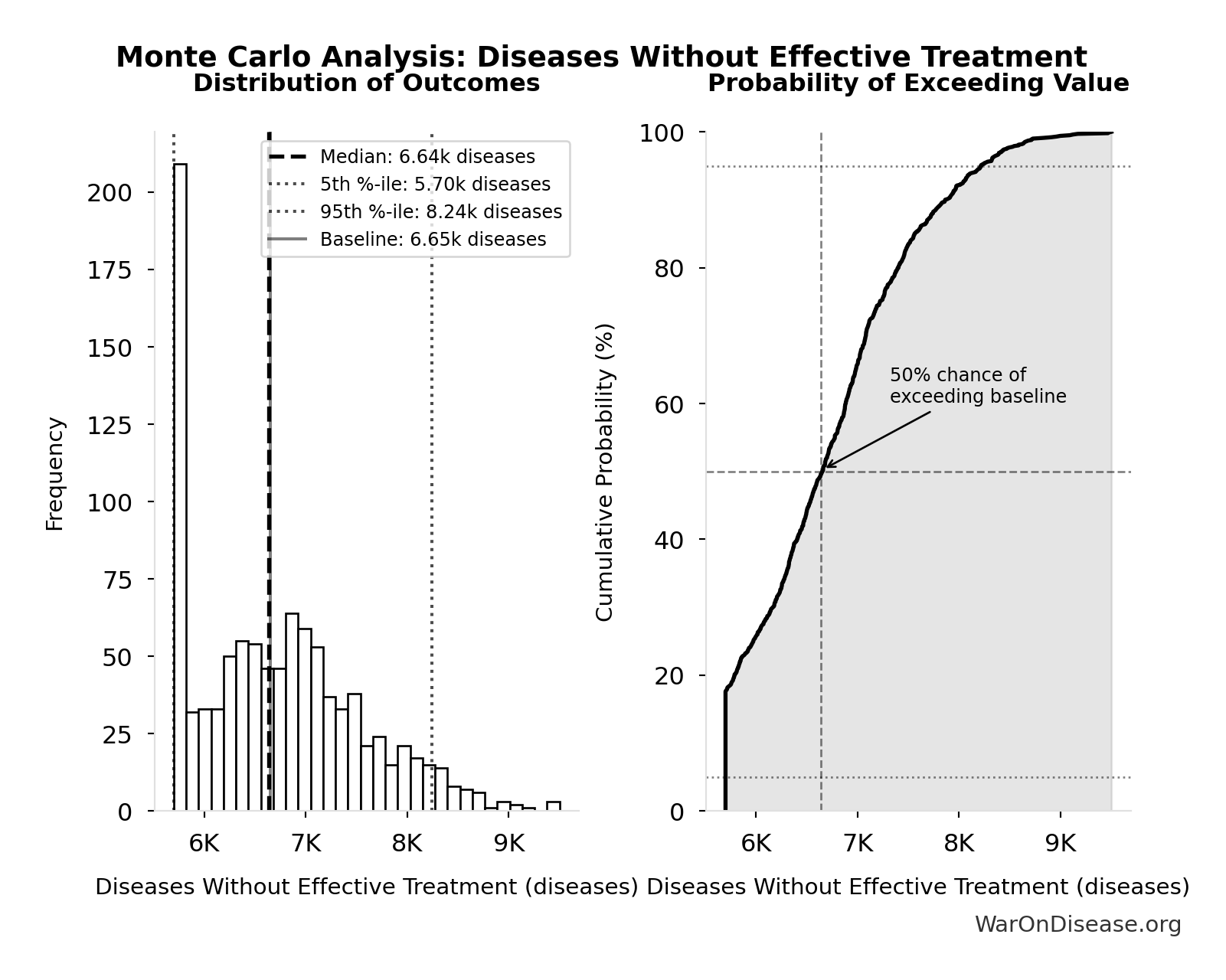
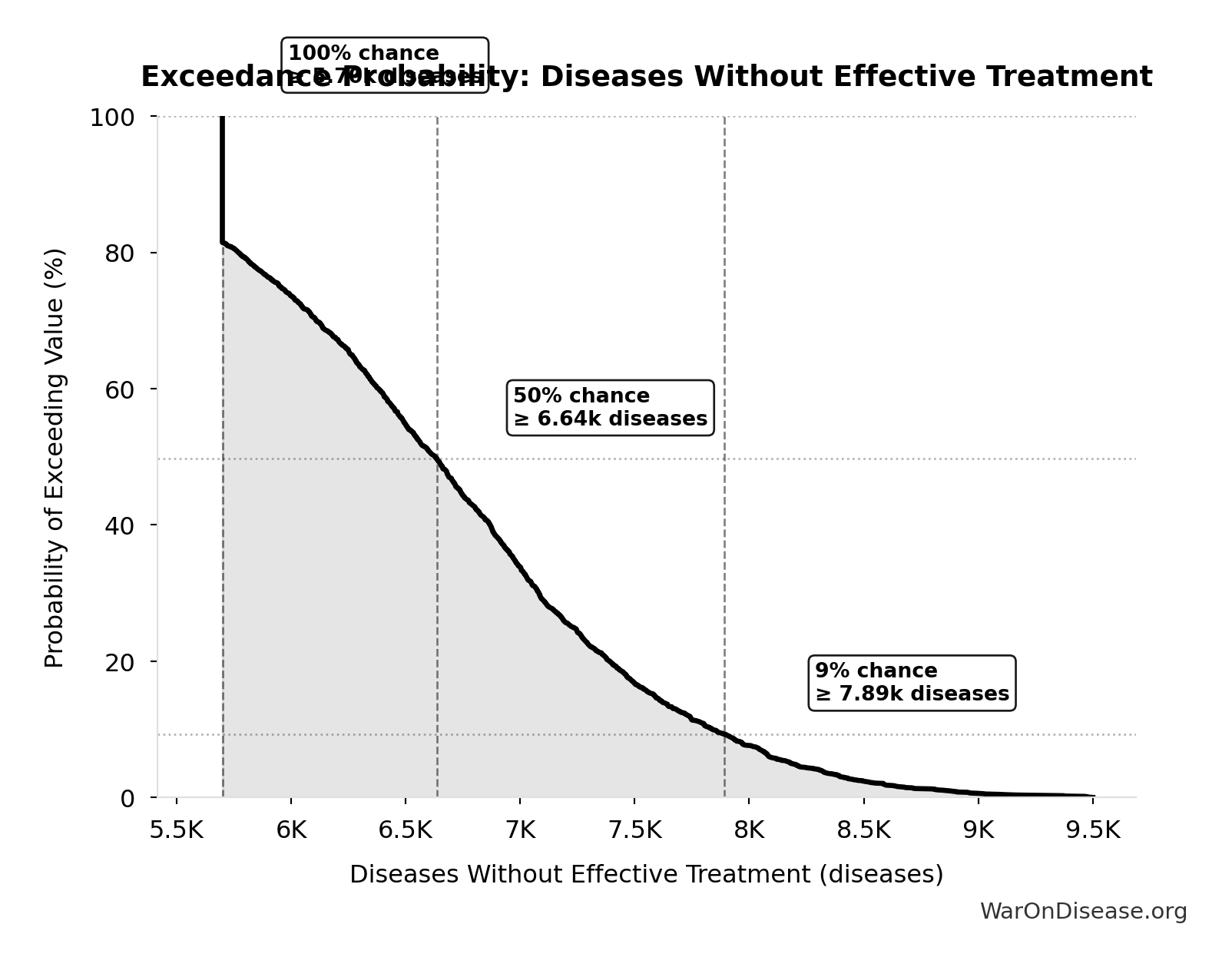
Diseases Without Effective Treatment: 6.65k diseases
Noteπ Details
Number of diseases without effective treatment. 95% of 7,000 rare diseases lack FDA-approved treatment (per Orphanet 2024). This is the βqueueβ of diseases waiting for cures.
Inputs:
- Total Number of Rare Diseases Globally π: 7.00k diseases (95% CI: 6.00k diseases - 10.0k diseases)
\[ \begin{gathered} N_{untreated} \\ = N_{rare} \times 0.95 \\ = 7{,}000 \times 0.95 \\ = 6{,}650 \end{gathered} \]
Methodology:142
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Diseases Without Effective Treatment
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Rare Diseases Count Global | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Diseases Without Effective Treatment
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 6.65k |
| Mean (expected value) | 6.73k |
| Median (50th percentile) | 6.64k |
| Standard Deviation | 835 |
| 90% Confidence Interval | [5.70k, 8.24k] |
The histogram shows the distribution of Diseases Without Effective Treatment across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Diseases Without Effective Treatment will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
Total Drugs Approved Since 1962: 3.10k drugs
Noteπ Details
Estimated total drugs approved globally since 1962 (62 years Γ average approval rate). Conservative: uses current rate, actual historical rate was lower in 1960s-80s.
Inputs:
- Average Annual New Drug Approvals Globally π: 50 drugs/year (95% CI: 45 drugs/year - 60 drugs/year)
\[ \begin{gathered} N_{drugs,62} \\ = Drugs_{ann,curr} \times 62 \\ = 50 \times 62 \\ = 3{,}100 \end{gathered} \]
Methodology:29
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Total Drugs Approved Since 1962
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Current Drug Approvals Per Year | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
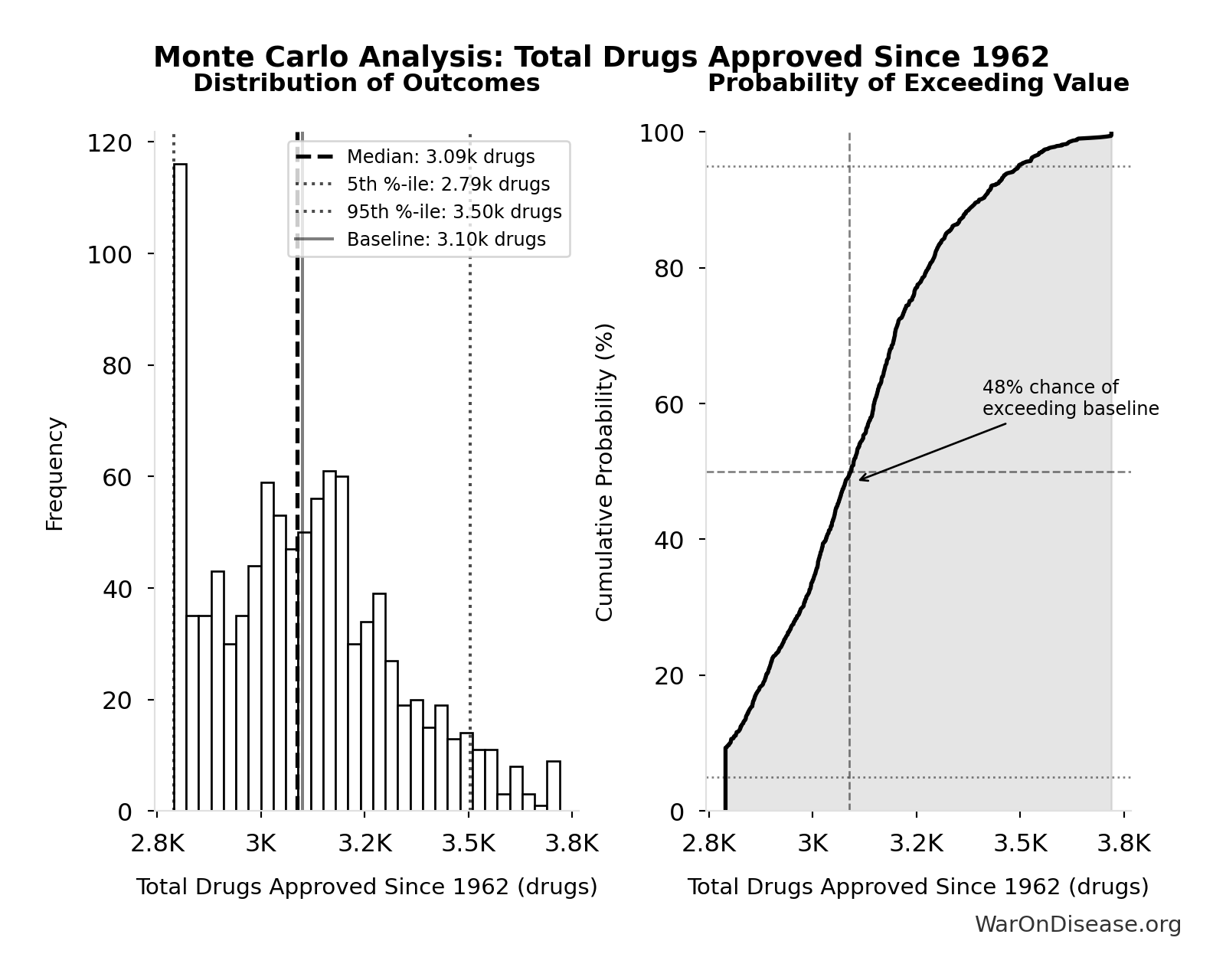
Simulation Results Summary: Total Drugs Approved Since 1962
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 3.10k |
| Mean (expected value) | 3.11k |
| Median (50th percentile) | 3.09k |
| Standard Deviation | 220 |
| 90% Confidence Interval | [2.79k, 3.50k] |
The histogram shows the distribution of Total Drugs Approved Since 1962 across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
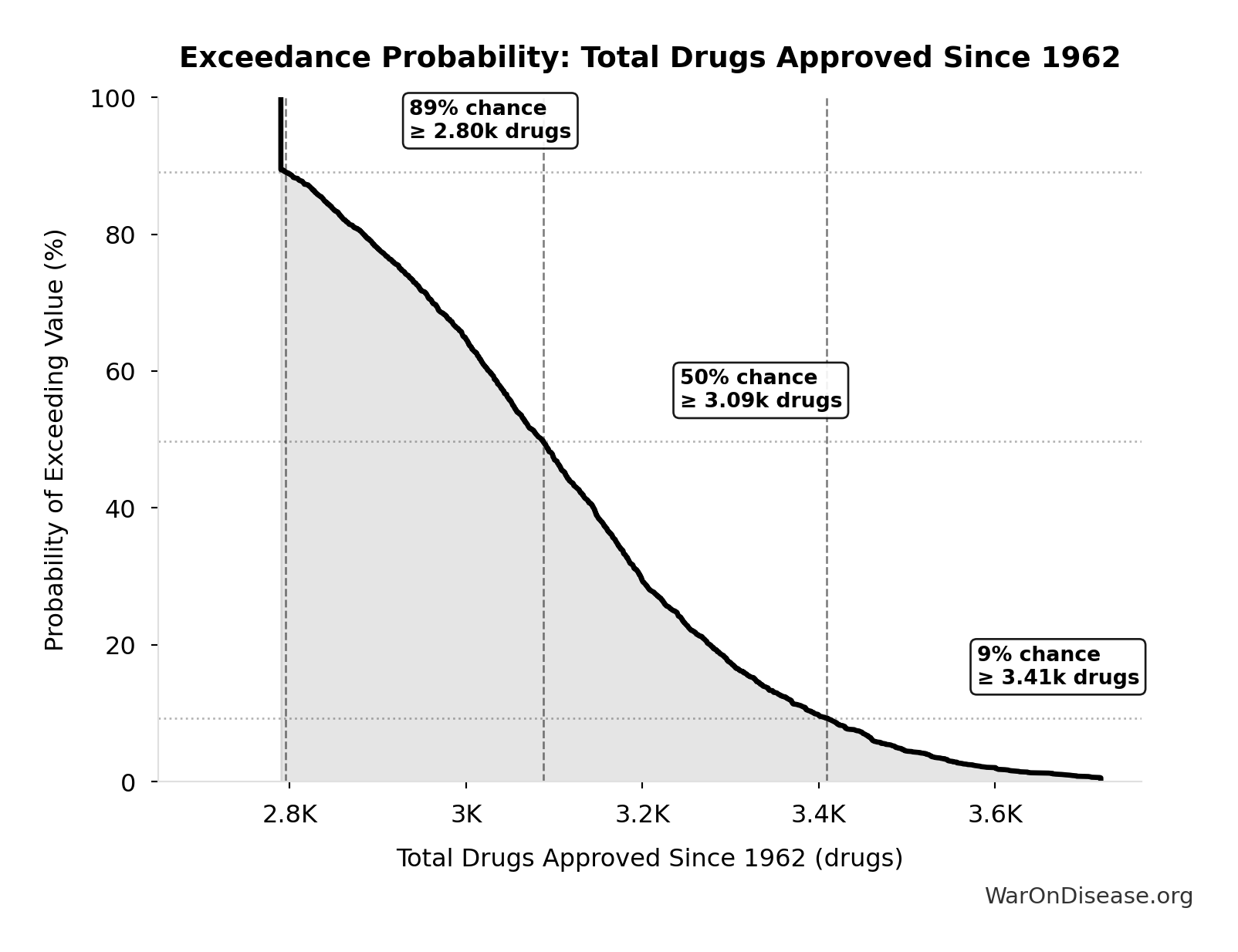
Exceedance Probability
This exceedance probability chart shows the likelihood that Total Drugs Approved Since 1962 will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
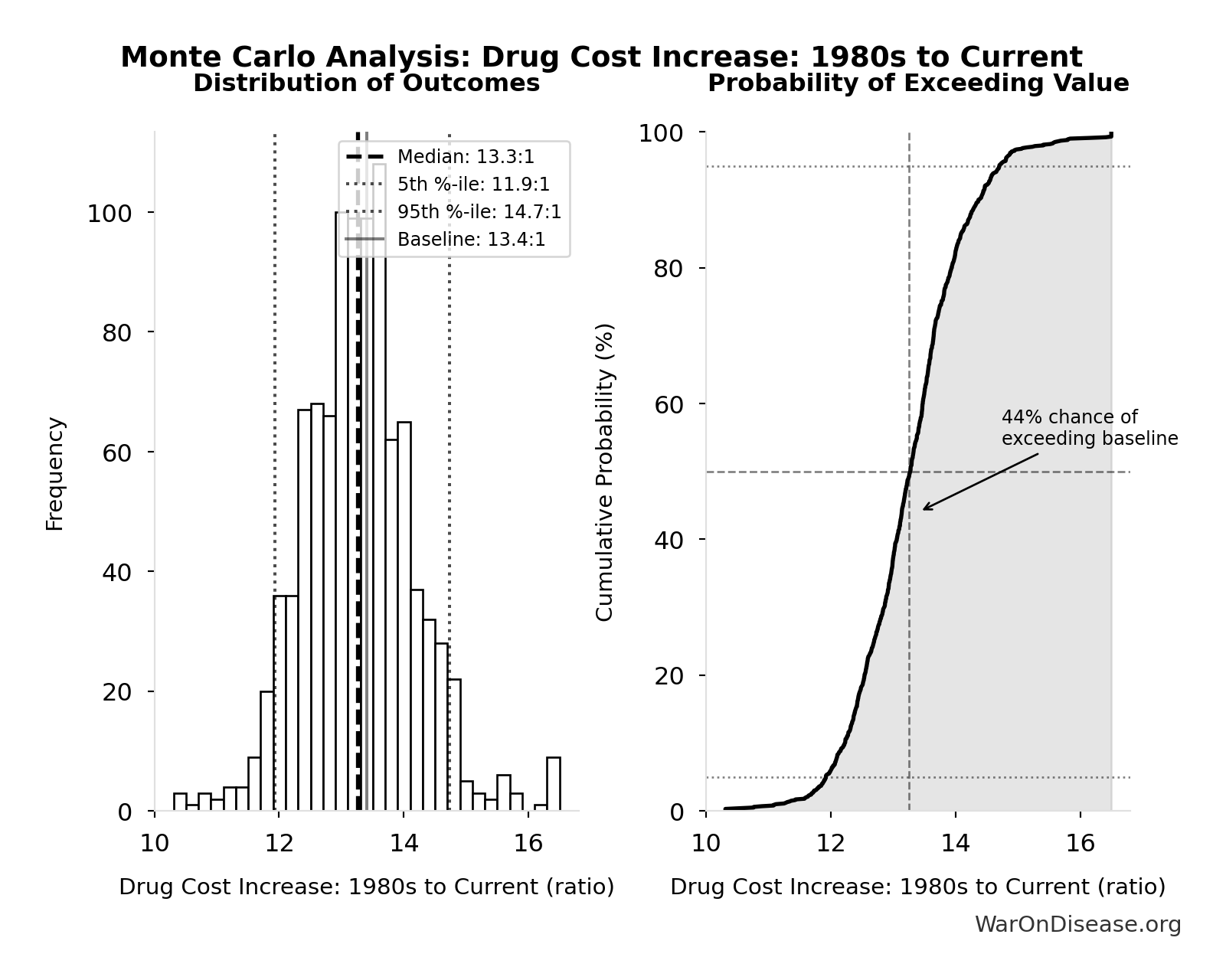
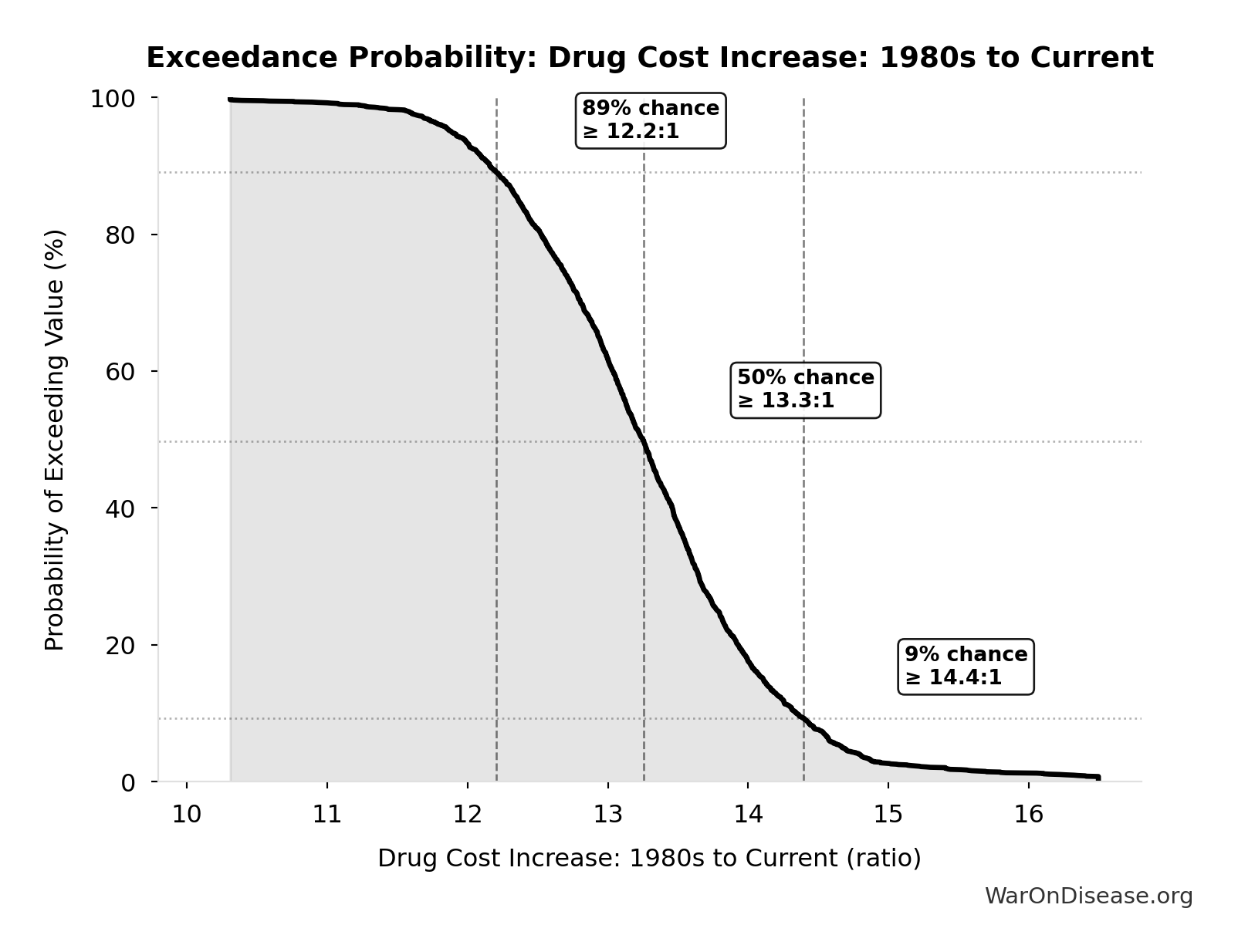
Drug Cost Increase: 1980s to Current: 13.4:1
Noteπ Details
Drug development cost increase from 1980s to current ($194M β $2.6B = 13.4x)
Inputs:
- Drug Development Cost (1980s) π: $194M (95% CI: $146M - $242M)
- Pharma Drug Development Cost (Current System) π: $2.60B (95% CI: $1.50B - $4B)
\[ \begin{gathered} k_{cost,80s} \\ = \frac{Cost_{dev,curr}}{Cost_{dev,80s}} \\ = \frac{\$2.6B}{\$194M} \\ = 13.4 \end{gathered} \]
Methodology:35
β High confidence
Sensitivity Analysis
Sensitivity Indices for Drug Cost Increase: 1980s to Current
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Pharma Drug Development Cost Current | 1.6909 | Strong driver |
| Drug Development Cost 1980s | -0.7048 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Drug Cost Increase: 1980s to Current
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 13.4:1 |
| Mean (expected value) | 13.3:1 |
| Median (50th percentile) | 13.3:1 |
| Standard Deviation | 0.915:1 |
| 90% Confidence Interval | [11.9:1, 14.7:1] |
The histogram shows the distribution of Drug Cost Increase: 1980s to Current across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Drug Cost Increase: 1980s to Current will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
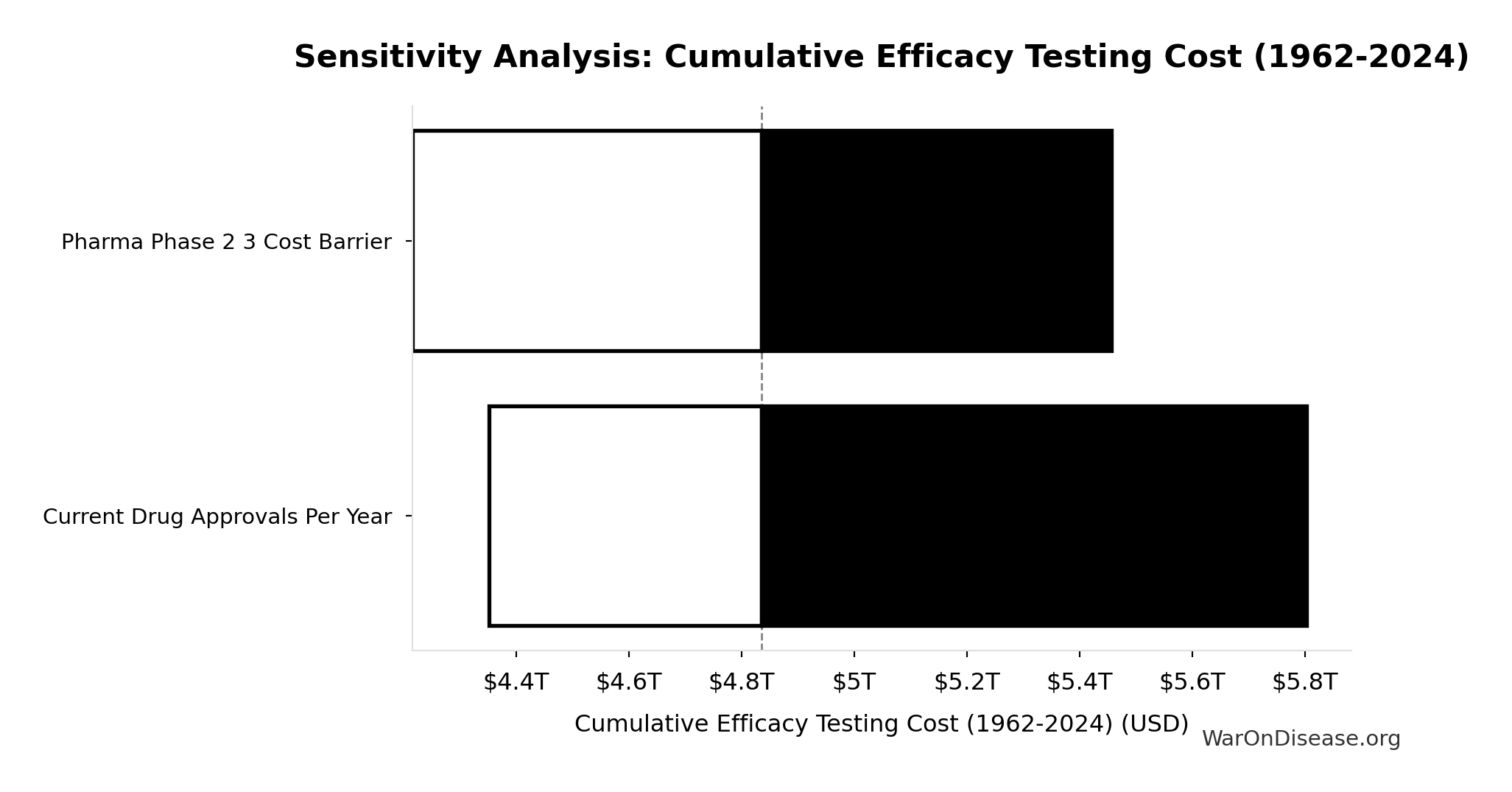
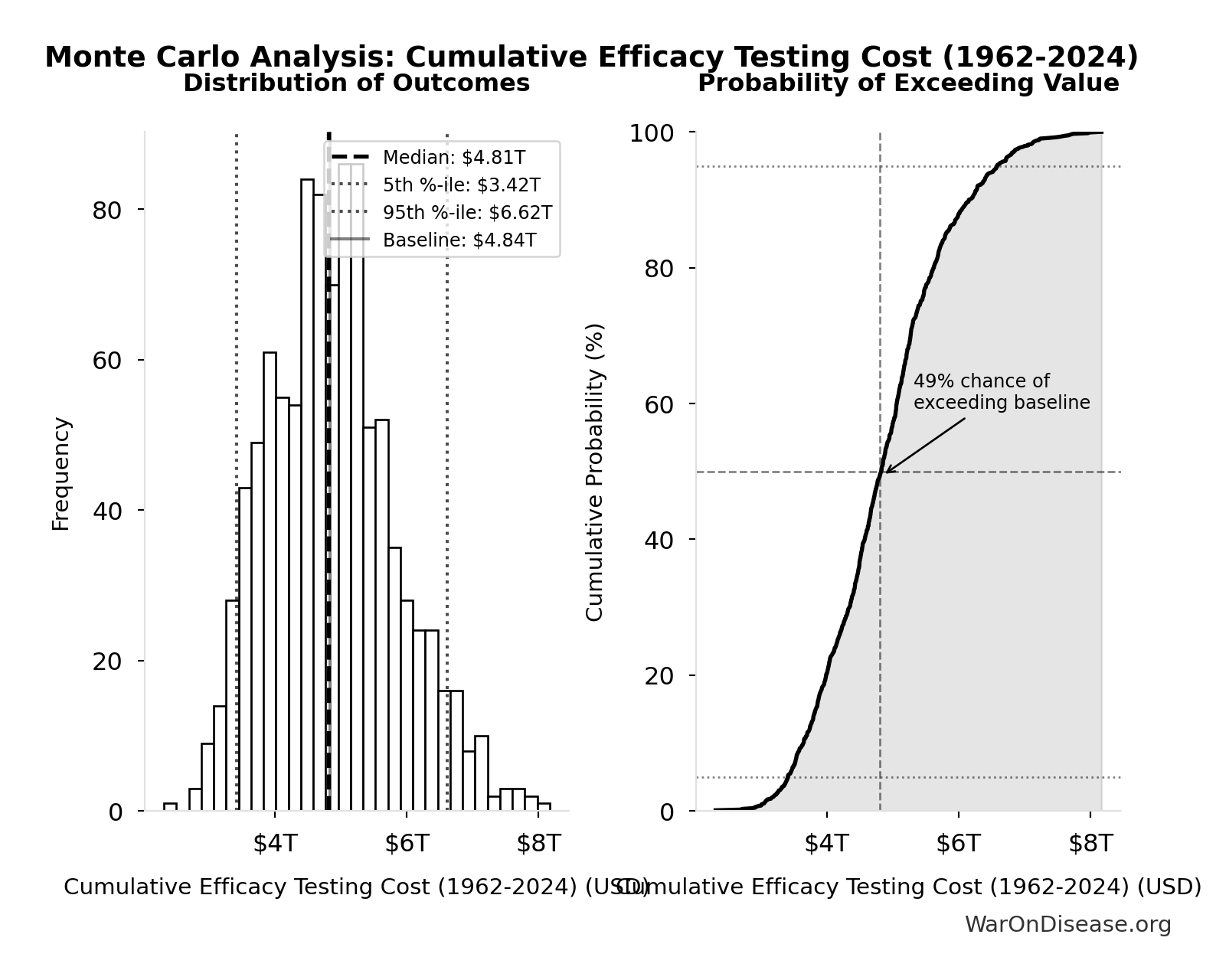
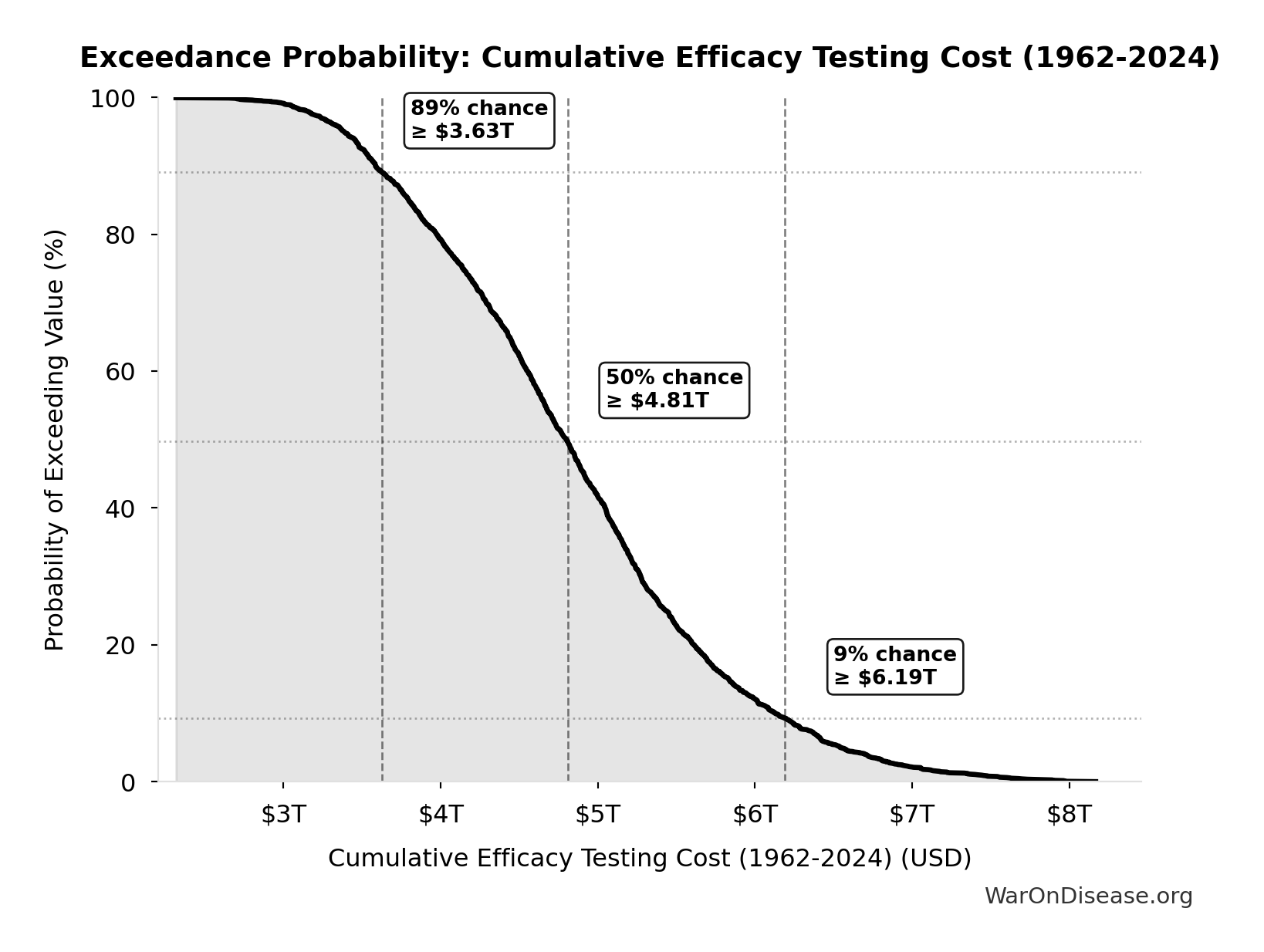
Cumulative Efficacy Testing Cost (1962-2024): $4.84T
Noteπ Details
Cumulative Phase 2/3 efficacy testing cost since 1962. Uses direct Phase 2/3 cost ($1.56B per drug) - this is a LOWER BOUND because it excludes opportunity cost of 8.2-year delays, compounds abandoned due to cost barrier, and regulatory overhead. Comparable to the $8 trillion spent on post-9/11 wars.
Inputs:
- Pharma Phase 2/3 Cost Barrier Per Drug: $1.56B (SE: Β±$200M)
- Total Drugs Approved Since 1962 π’: 3.10k drugs
\[ \begin{gathered} Cost_{eff,cumul} \\ = Cost_{P2+P3} \times N_{drugs,62} \\ = \$1.56B \times 3{,}100 \\ = \$4.84T \\[0.5em] \text{where } N_{drugs,62} = Drugs_{ann,curr} \times 62 = 50 \times 62 = 3{,}100 \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#scale
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Cumulative Efficacy Testing Cost (1962-2024)
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Drugs Approved Since 1962 | 0.5385 | Strong driver |
| Pharma Phase 2 3 Cost Barrier | 0.4652 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Cumulative Efficacy Testing Cost (1962-2024)
| Statistic | Value |
|---|---|
| Baseline (deterministic) | $4.84T |
| Mean (expected value) | $4.88T |
| Median (50th percentile) | $4.81T |
| Standard Deviation | $977B |
| 90% Confidence Interval | [$3.42T, $6.62T] |
The histogram shows the distribution of Cumulative Efficacy Testing Cost (1962-2024) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Cumulative Efficacy Testing Cost (1962-2024) will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
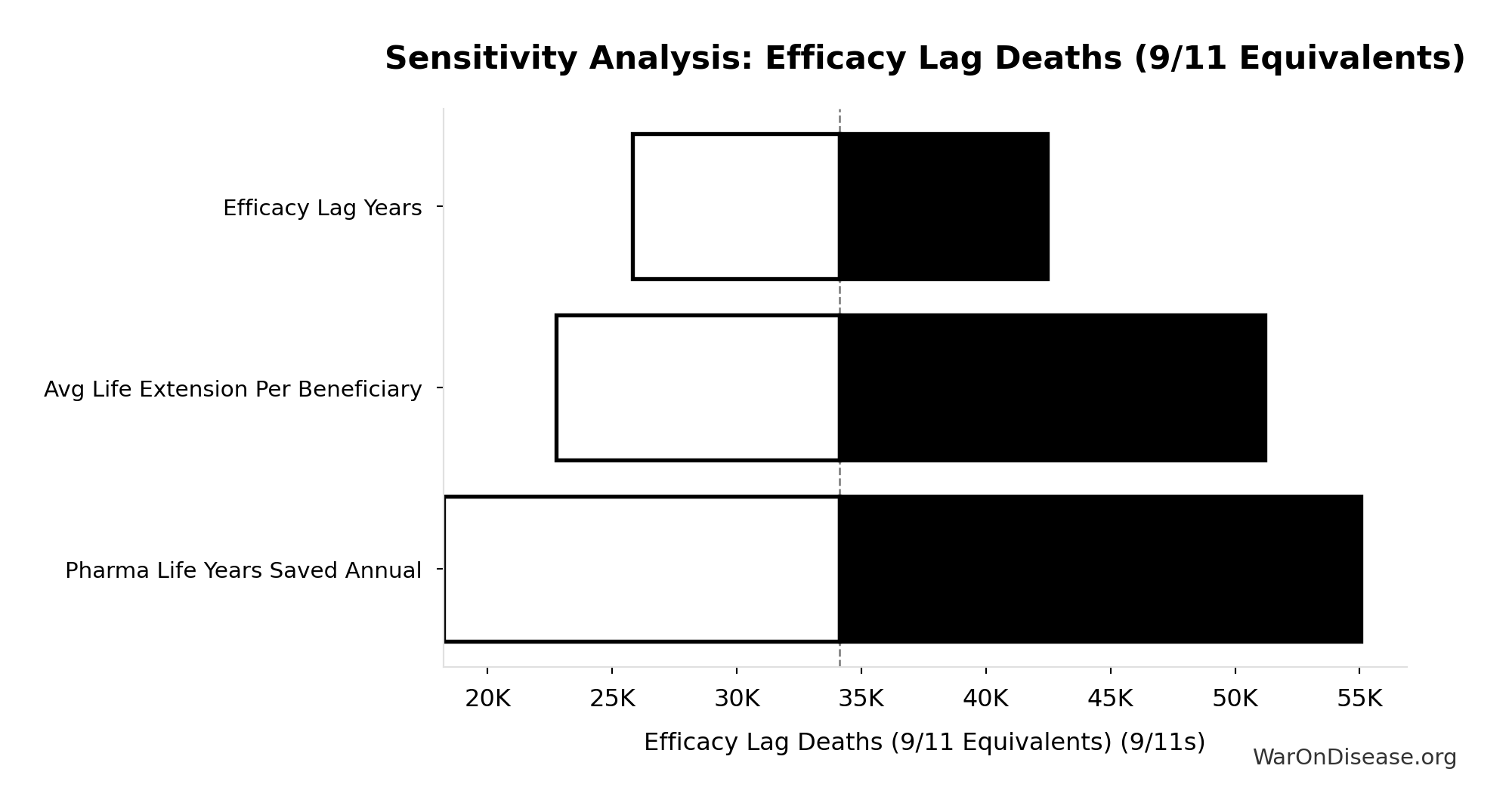
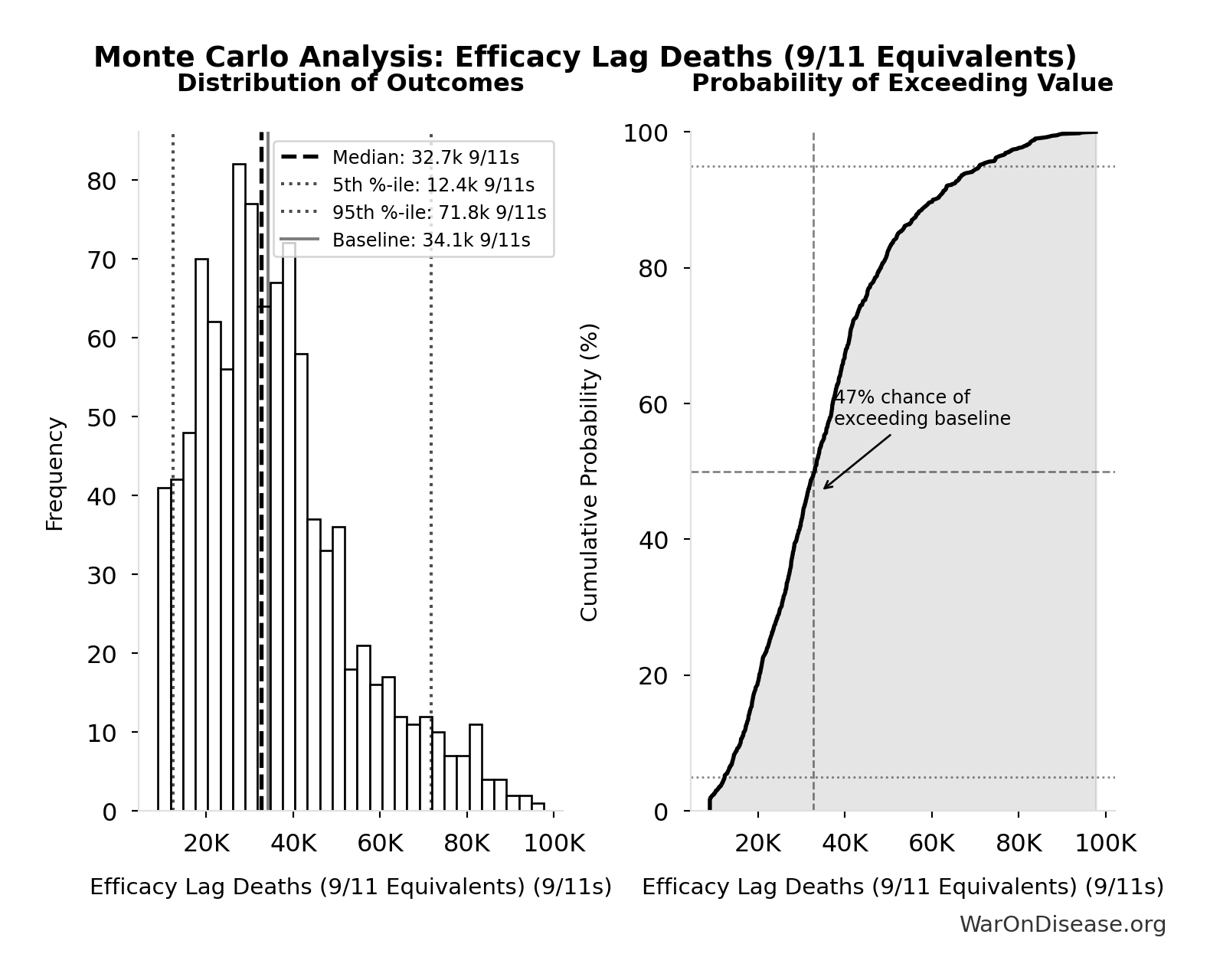
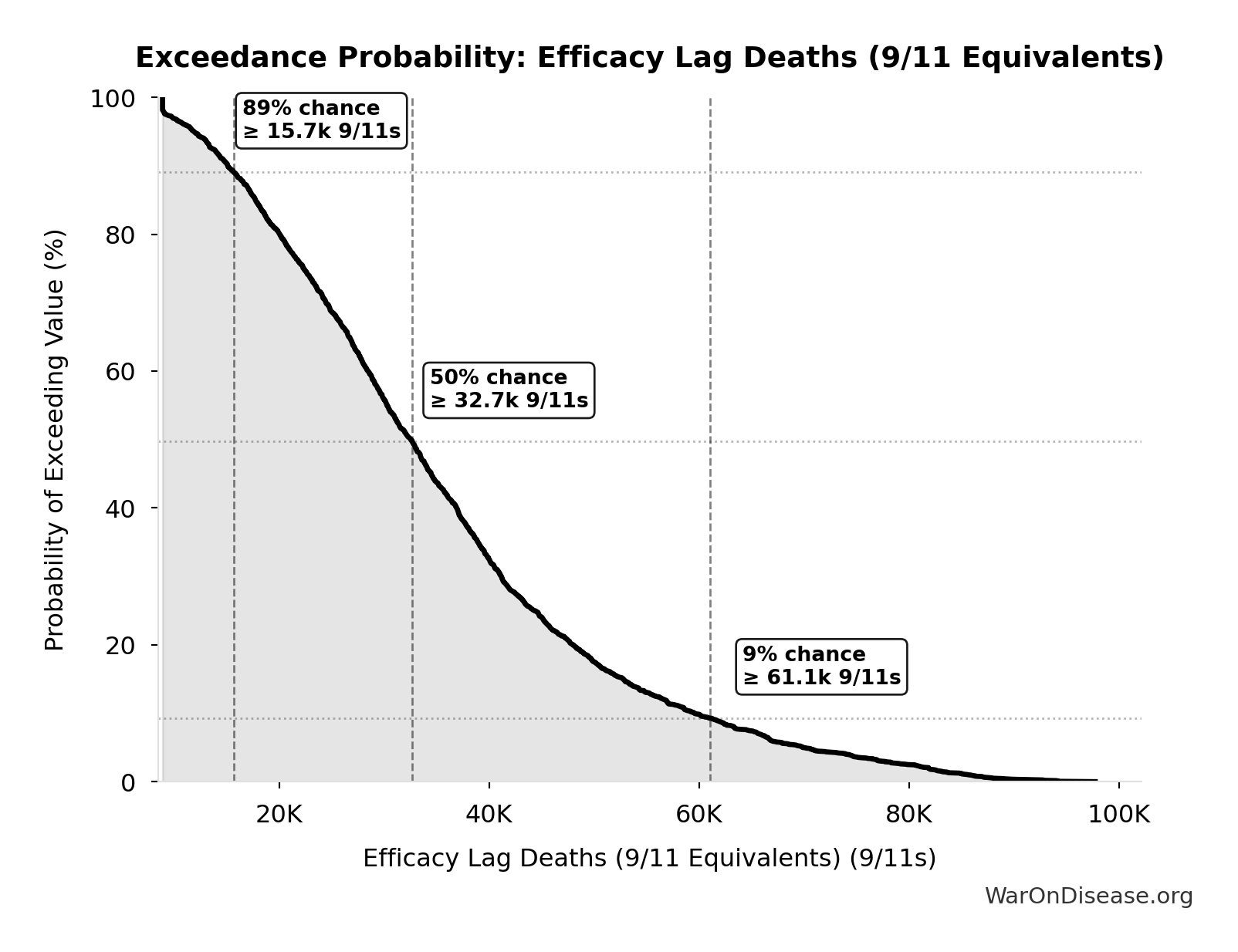
Efficacy Lag Deaths (9/11 Equivalents): 34.1k 9/11s
Noteπ Details
Total deaths from efficacy lag expressed in 9/11 equivalents. Makes the mortality cost viscerally understandable: how many September 11ths worth of deaths did the 1962 efficacy requirements cause?
Inputs:
- Total Deaths from Historical Progress Delays π’: 102M deaths
- September 11 Deaths π: 2.98k people
\[ \begin{gathered} N_{9/11,equiv} = \frac{Deaths_{lag,total}}{N_{9/11}} = \frac{102M}{2{,}980} = 34{,}100 \\[0.5em] \text{where } Deaths_{lag,total} \\ = Lives_{saved,annual} \times T_{lag} \\ = 12.4M \times 8.2 \\ = 102M \\[0.5em] \text{where } Lives_{saved,annual} = \frac{LY_{saved,annual}}{T_{ext}} = \frac{149M}{12} = 12.4M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#scale
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Efficacy Lag Deaths (9/11 Equivalents)
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Existing Drugs Efficacy Lag Deaths Total | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Efficacy Lag Deaths (9/11 Equivalents)
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 34.1k |
| Mean (expected value) | 36.0k |
| Median (50th percentile) | 32.7k |
| Standard Deviation | 17.8k |
| 90% Confidence Interval | [12.4k, 71.8k] |
The histogram shows the distribution of Efficacy Lag Deaths (9/11 Equivalents) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Efficacy Lag Deaths (9/11 Equivalents) will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
Treatment Delay YLD - Annual: 2.01B DALYs
Noteπ Details
Annual YLD from treatment delay: patients receiving chronic disease treatment would have collectively avoided this disability if treatments were available 8.2 years earlier. Represents morbidity burden for treatment beneficiaries (distinct from mortality burden).
Inputs:
- Annual Chronic Disease Patients Treated π’: 982M people
- Regulatory Delay for Efficacy Testing Post-Safety Verification π: 8.2 years (SE: Β±2 years)
- Treatment Disability Reduction π: 0.25 weight (95% CI: 0.15 weight - 0.35 weight)
\[ \begin{gathered} YLD_{treat\_delay} \\ = N_{treated} \times T_{lag} \times \Delta DW_{treat} \\ = 982M \times 8.2 \times 0.25 \\ = 2.01B \\[0.5em] \text{where } N_{treated} \\ = DOT_{chronic} \times 0.000767 \\ = 1.28T \times 0.000767 \\ = 982M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#treatment-morbidity
? Low confidence
Sensitivity Analysis
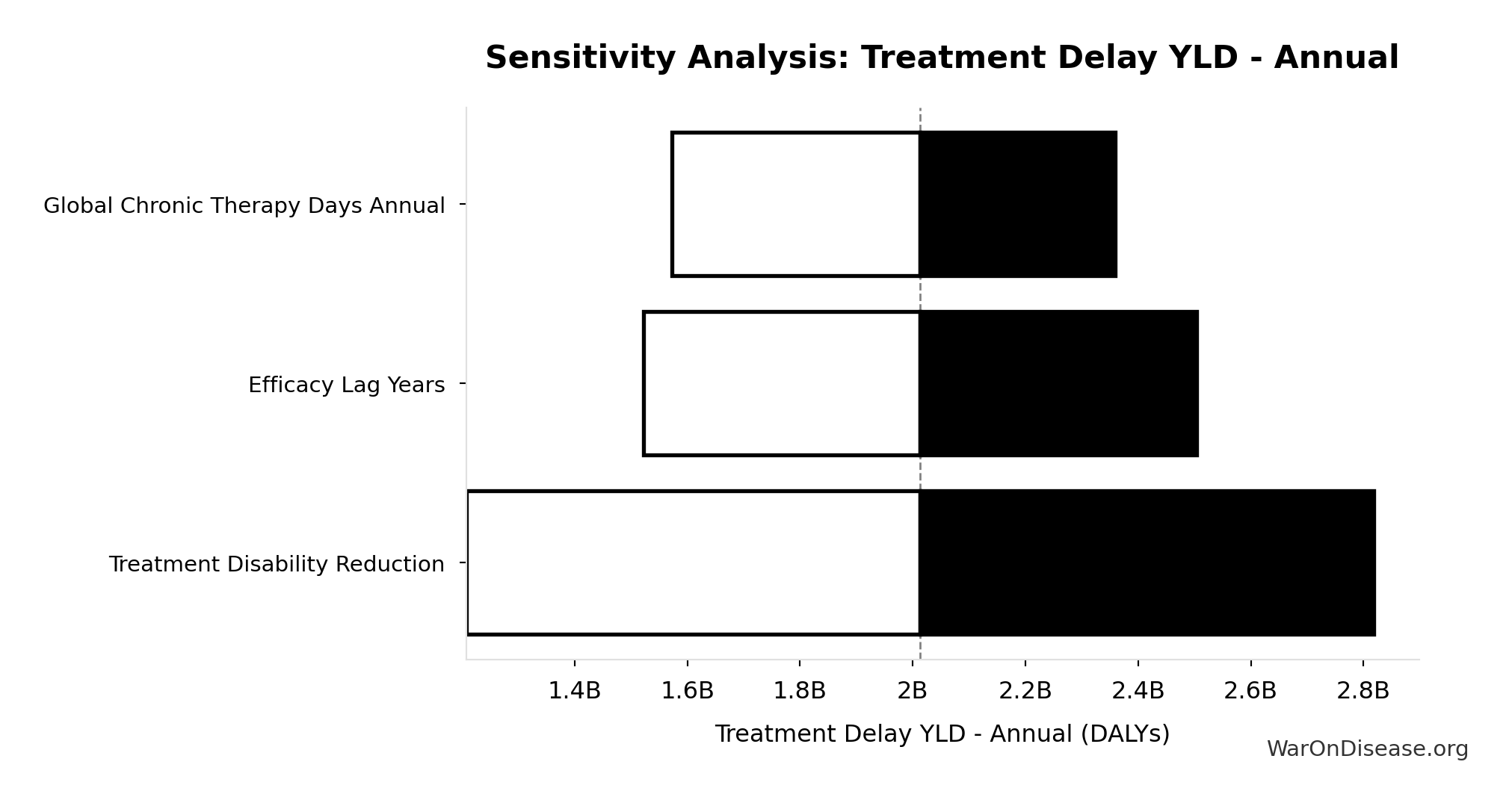
Sensitivity Indices for Treatment Delay YLD - Annual
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Chronic Disease Treated Patients Annual | 3.0959 | Strong driver |
| Treatment Disability Reduction | -2.4506 | Strong driver |
| Efficacy Lag Years | 0.3319 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
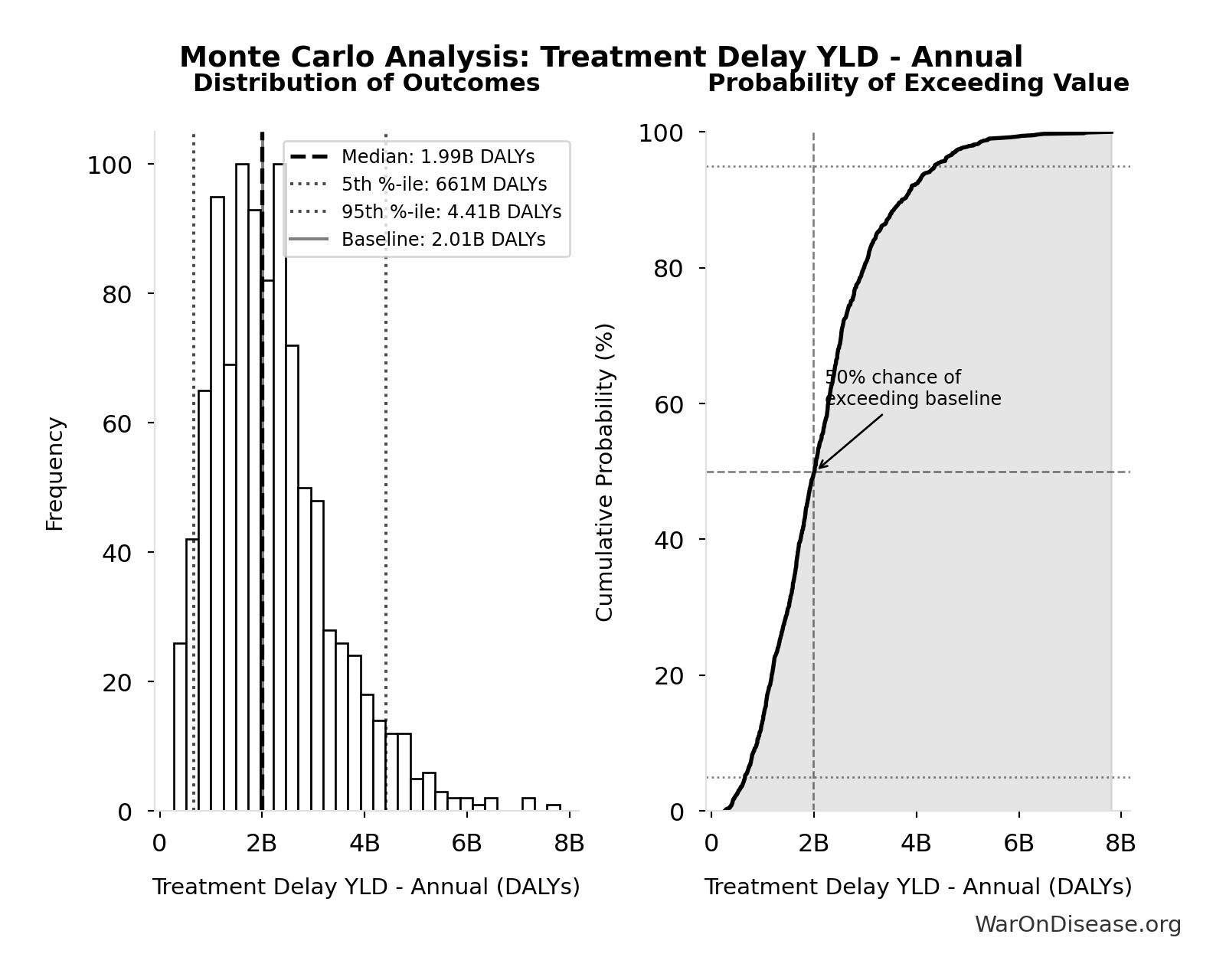
Monte Carlo Distribution
Simulation Results Summary: Treatment Delay YLD - Annual
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 2.01B |
| Mean (expected value) | 2.20B |
| Median (50th percentile) | 1.99B |
| Standard Deviation | 1.18B |
| 90% Confidence Interval | [661M, 4.41B] |
The histogram shows the distribution of Treatment Delay YLD - Annual across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
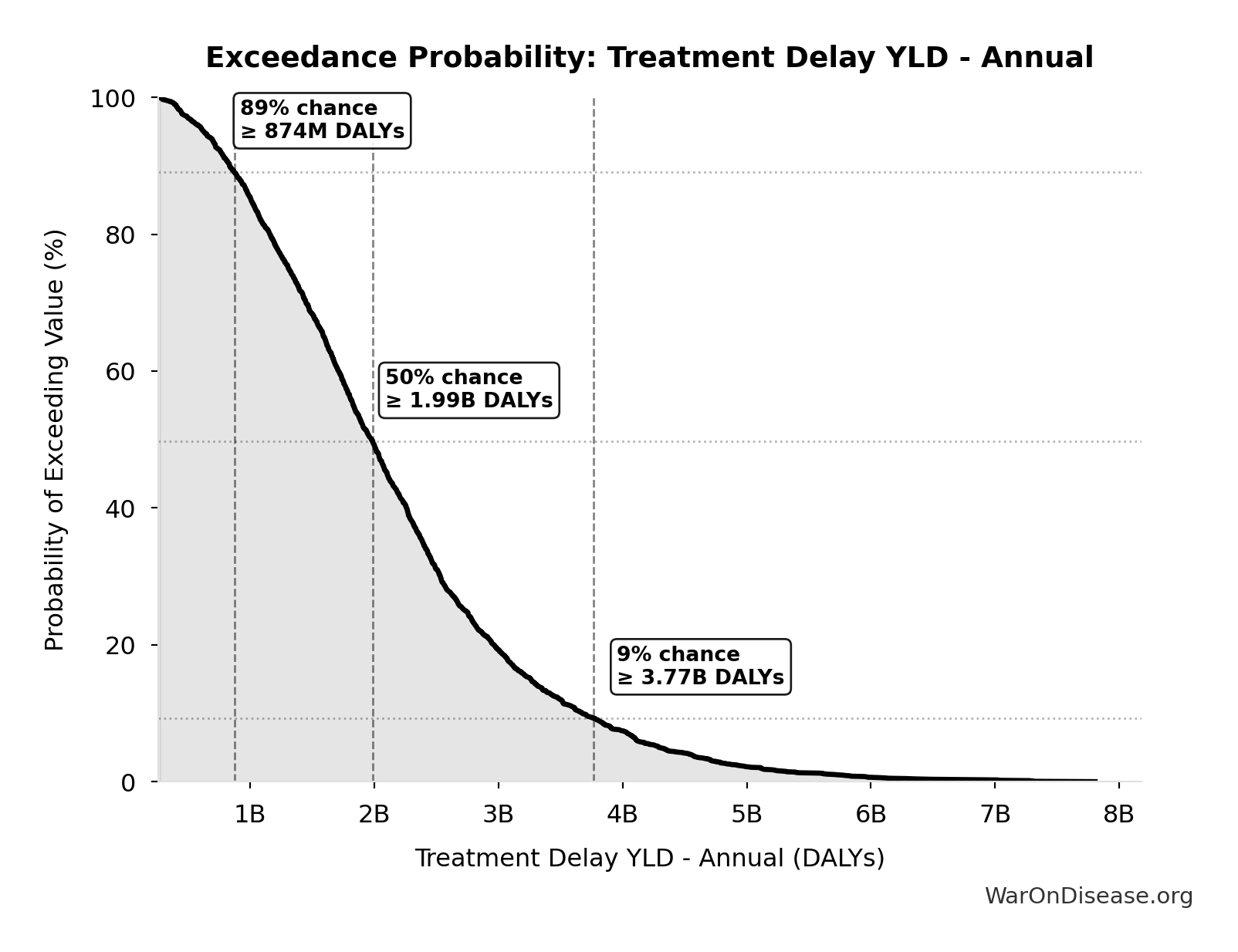
Exceedance Probability
This exceedance probability chart shows the likelihood that Treatment Delay YLD - Annual will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
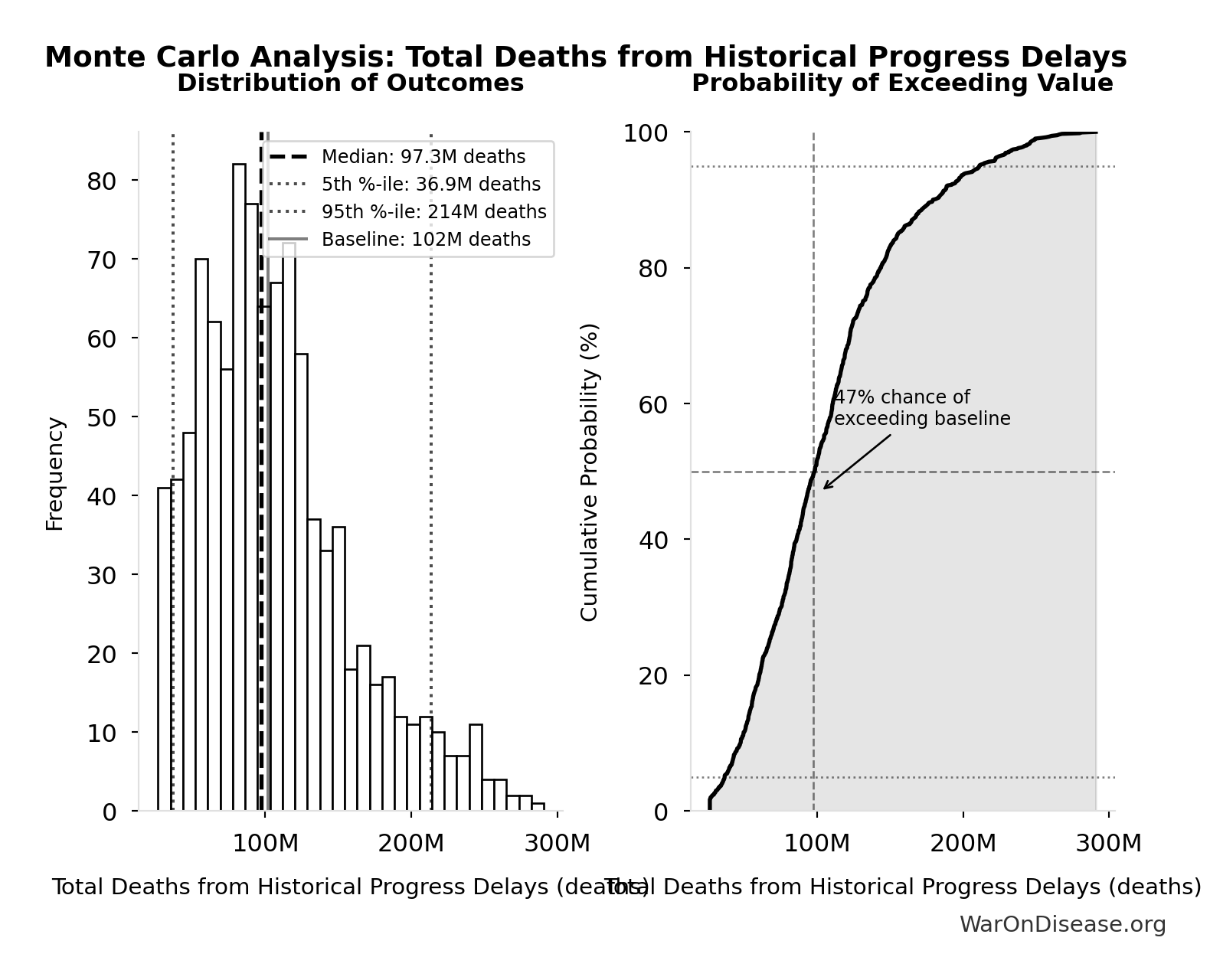
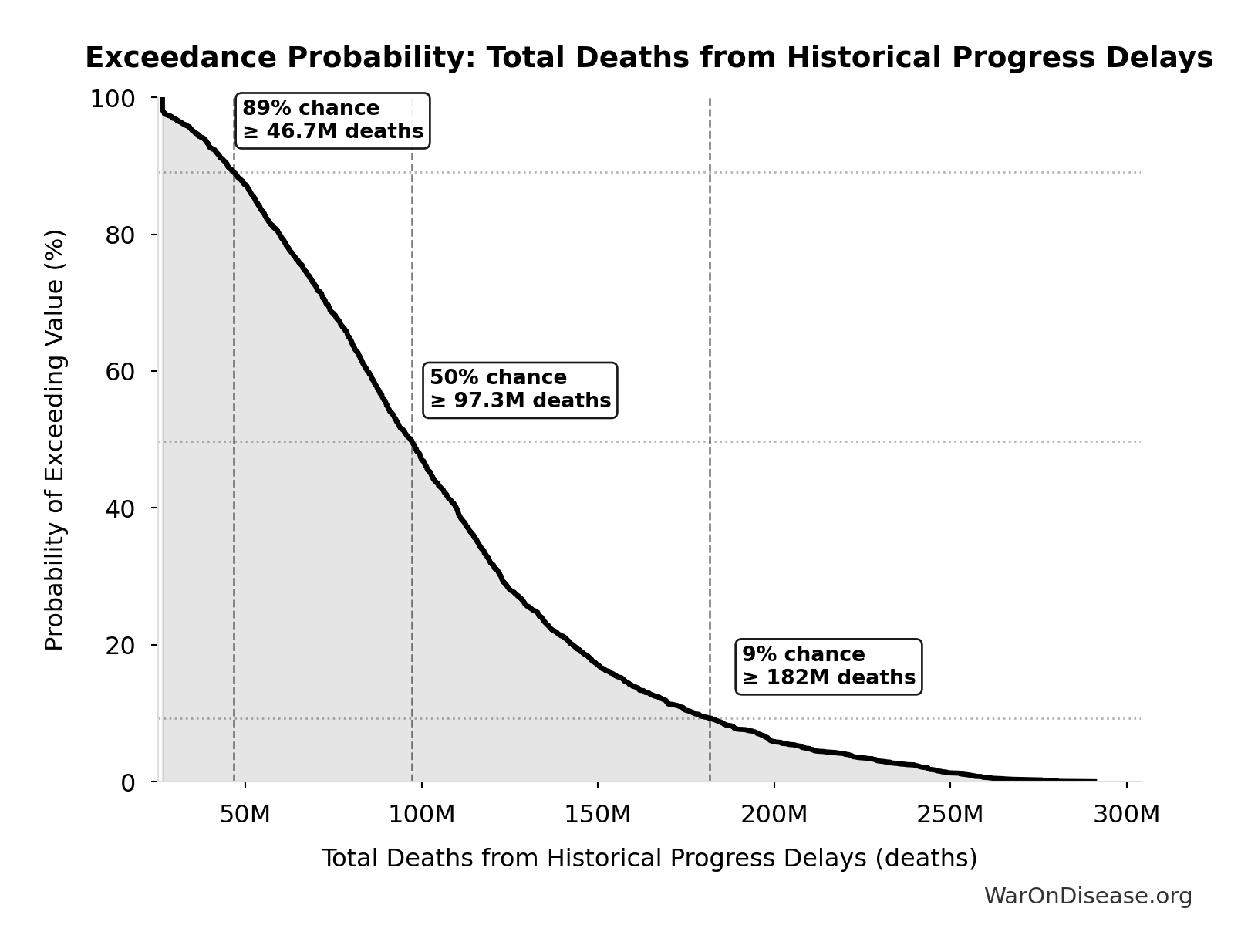
Total Deaths from Historical Progress Delays: 102M deaths
Noteπ Details
Total deaths from delaying existing drugs over 8.2-year efficacy lag. One-time impact of eliminating Phase 2-4 testing delay for drugs already approved 1962-2024. Based on Lichtenberg (2019) estimate of 12M lives saved annually Γ 8.2 years efficacy lag. Excludes innovation acceleration effects.
Inputs:
- Annual Lives Saved by Pharmaceuticals π’: 12.4M deaths
- Regulatory Delay for Efficacy Testing Post-Safety Verification π: 8.2 years (SE: Β±2 years)
\[ \begin{gathered} Deaths_{lag,total} \\ = Lives_{saved,annual} \times T_{lag} \\ = 12.4M \times 8.2 \\ = 102M \\[0.5em] \text{where } Lives_{saved,annual} = \frac{LY_{saved,annual}}{T_{ext}} = \frac{149M}{12} = 12.4M \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#historical-progress
~ Medium confidence
Sensitivity Analysis
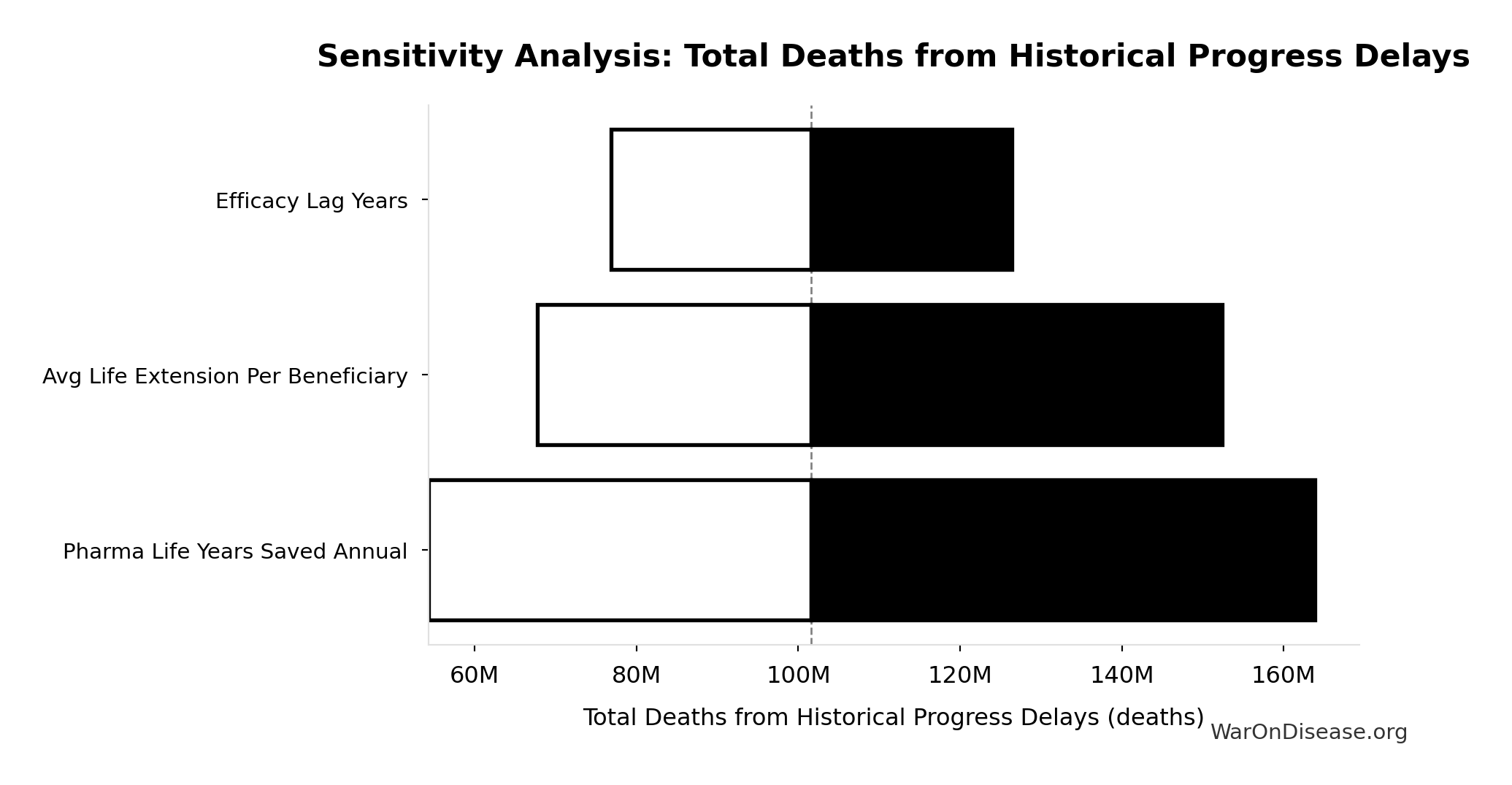
Sensitivity Indices for Total Deaths from Historical Progress Delays
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Pharma Lives Saved Annual | 1.2721 | Strong driver |
| Efficacy Lag Years | -0.2811 | Weak driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Total Deaths from Historical Progress Delays
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 102M |
| Mean (expected value) | 107M |
| Median (50th percentile) | 97.3M |
| Standard Deviation | 53.0M |
| 90% Confidence Interval | [36.9M, 214M] |
The histogram shows the distribution of Total Deaths from Historical Progress Delays across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Total Deaths from Historical Progress Delays will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
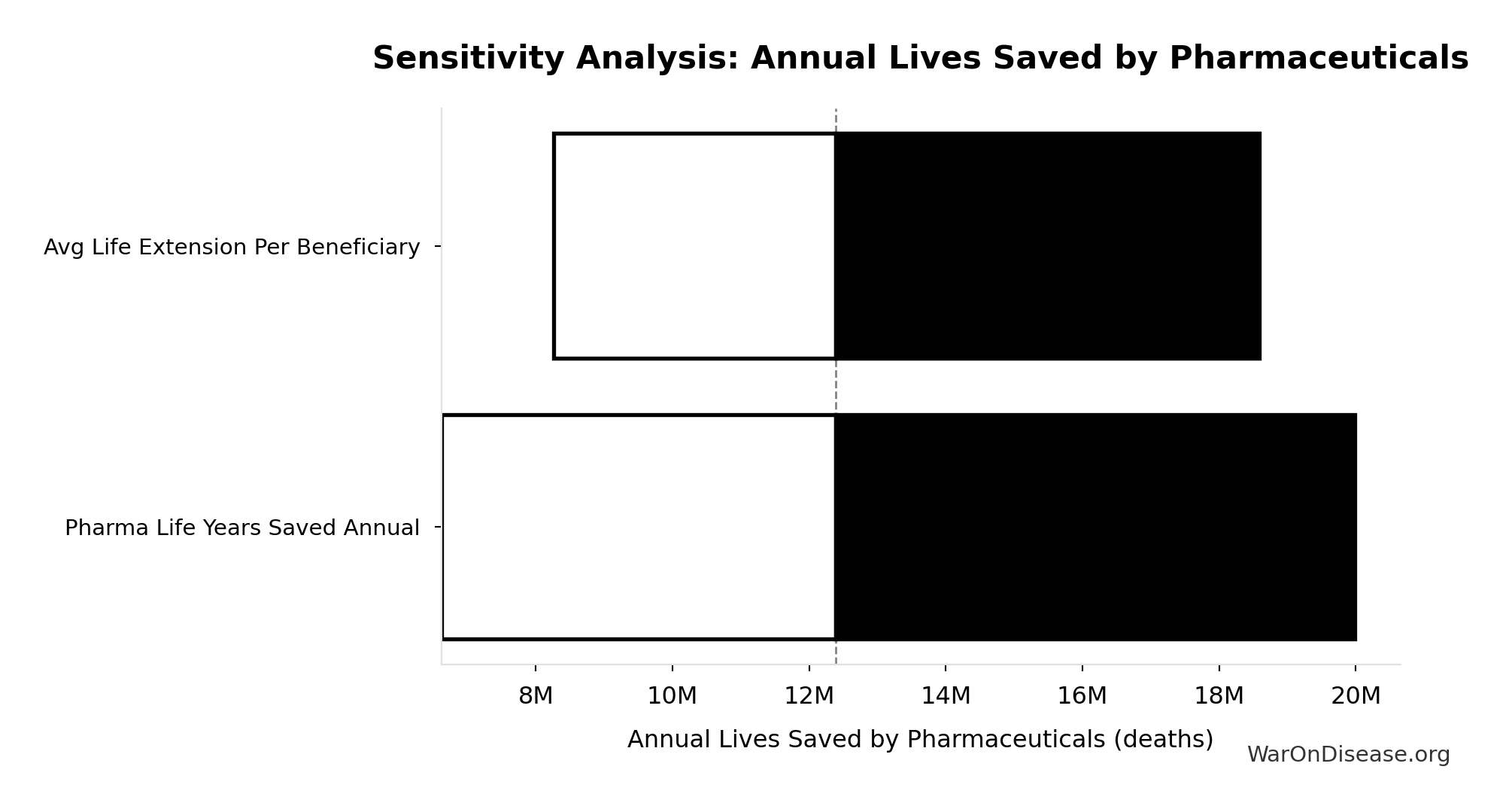
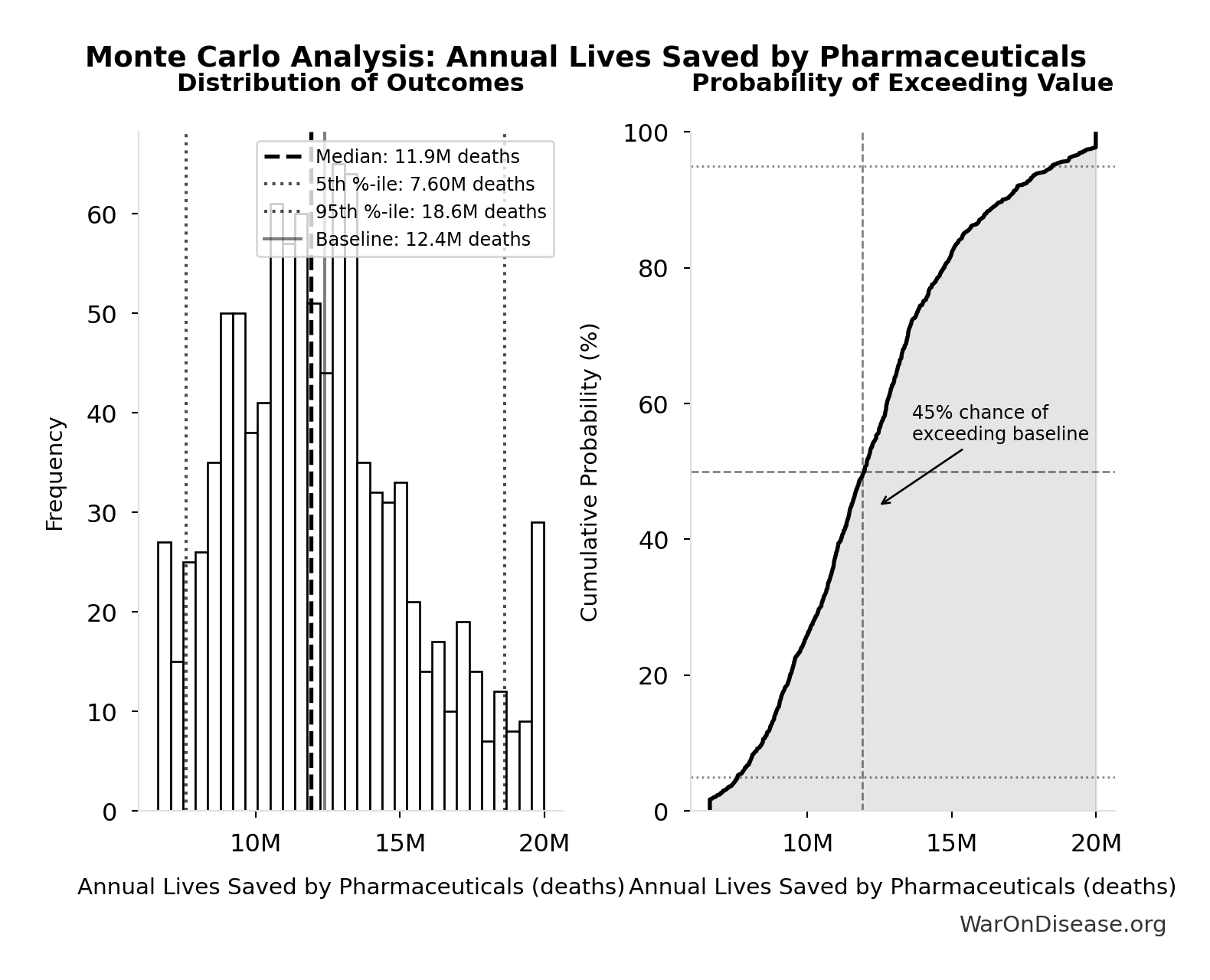
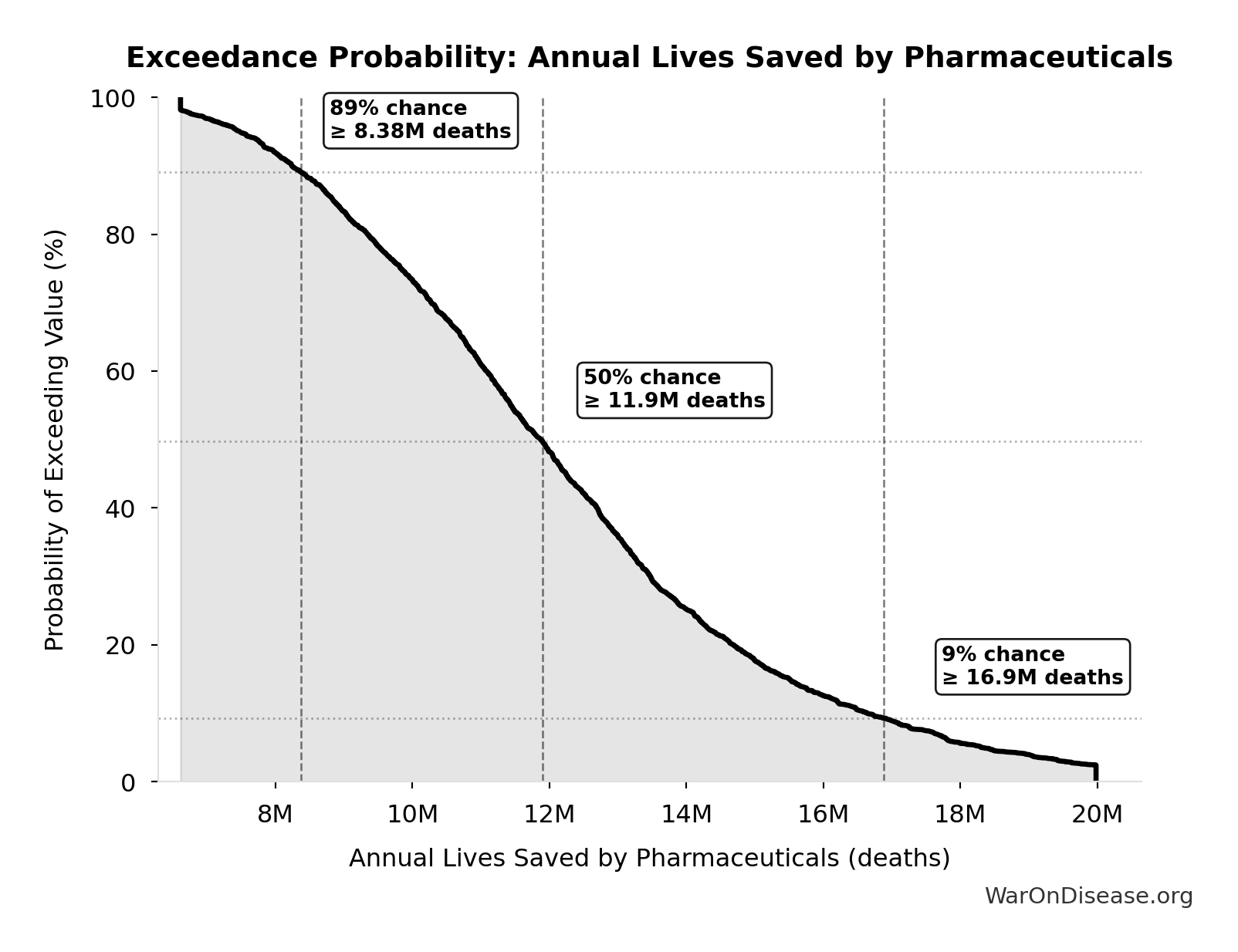
Annual Lives Saved by Pharmaceuticals: 12.4M deaths
Noteπ Details
Annual lives saved by pharmaceutical interventions globally. Derived from Lichtenberg (2019) finding of 148.7M life-years saved, divided by assumed 12-year average life extension per beneficiary. Note: Life-years is the primary metric; lives is an approximation for intuitive communication.
Inputs:
- Annual Life-Years Saved by Pharmaceuticals π: 149M life-years (95% CI: 79.4M life-years - 240M life-years)
- Average Life Extension per Beneficiary: 12 years (95% CI: 8 years - 18 years)
\[ \begin{gathered} Lives_{saved,annual} \\ = \frac{LY_{saved,annual}}{T_{ext}} \\ = \frac{149M}{12} \\ = 12.4M \end{gathered} \]
Methodology:84
? Low confidence
Sensitivity Analysis
Sensitivity Indices for Annual Lives Saved by Pharmaceuticals
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Pharma Life Years Saved Annual | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Annual Lives Saved by Pharmaceuticals
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 12.4M |
| Mean (expected value) | 12.3M |
| Median (50th percentile) | 11.9M |
| Standard Deviation | 3.20M |
| 90% Confidence Interval | [7.60M, 18.6M] |
The histogram shows the distribution of Annual Lives Saved by Pharmaceuticals across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Annual Lives Saved by Pharmaceuticals will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
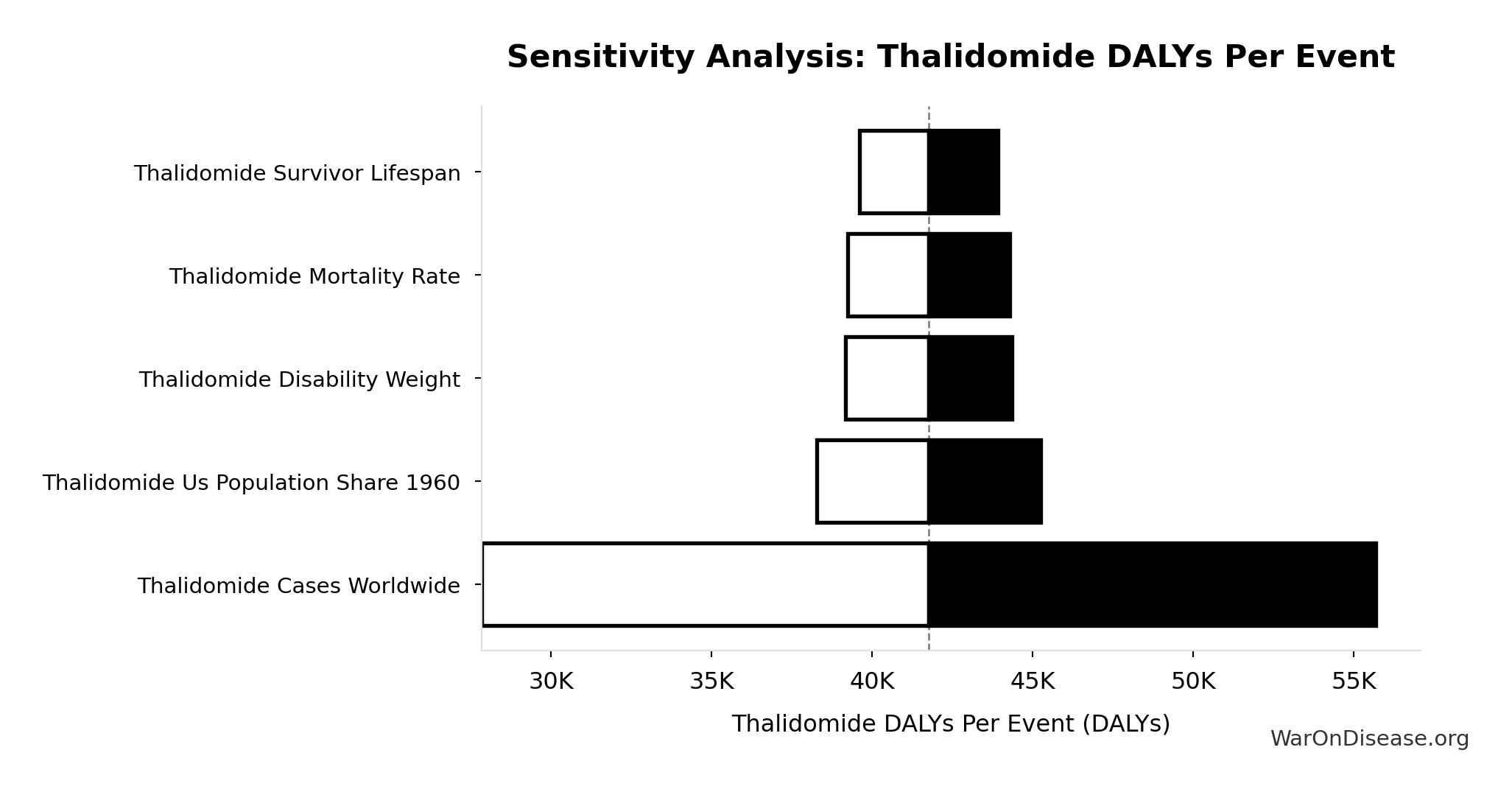
Thalidomide DALYs Per Event: 41.8k DALYs
Noteπ Details
Total DALYs per US-scale thalidomide event (YLL + YLD)
Inputs:
- Thalidomide YLD Per Event π’: 13.0k years
- Thalidomide YLL Per Event π’: 28.8k years
\[ \begin{gathered} DALY_{thal} \\ = YLD_{thal} + YLL_{thal} \\ = 13{,}000 + 28{,}800 \\ = 41{,}800 \\[0.5em] \text{where } YLD_{thal} \\ = DW_{thal} \times N_{thal,survive} \times LE_{thal} \\ = 0.4 \times 540 \times 60 \\ = 13{,}000 \\[0.5em] \text{where } N_{thal,survive} \\ = N_{thal,US,prevent} \times (1 - Rate_{thal,mort}) \\ = 900 \times (1 - 40\%) \\ = 540 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \\[0.5em] \text{where } YLL_{thal} = Deaths_{thal} \times 80 = 360 \times 80 = 28{,}800 \\[0.5em] \text{where } Deaths_{thal} \\ = Rate_{thal,mort} \times N_{thal,US,prevent} \\ = 40\% \times 900 \\ = 360 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Thalidomide DALYs Per Event
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide Yll Per Event | 0.6300 | Strong driver |
| Thalidomide Yld Per Event | 0.3701 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
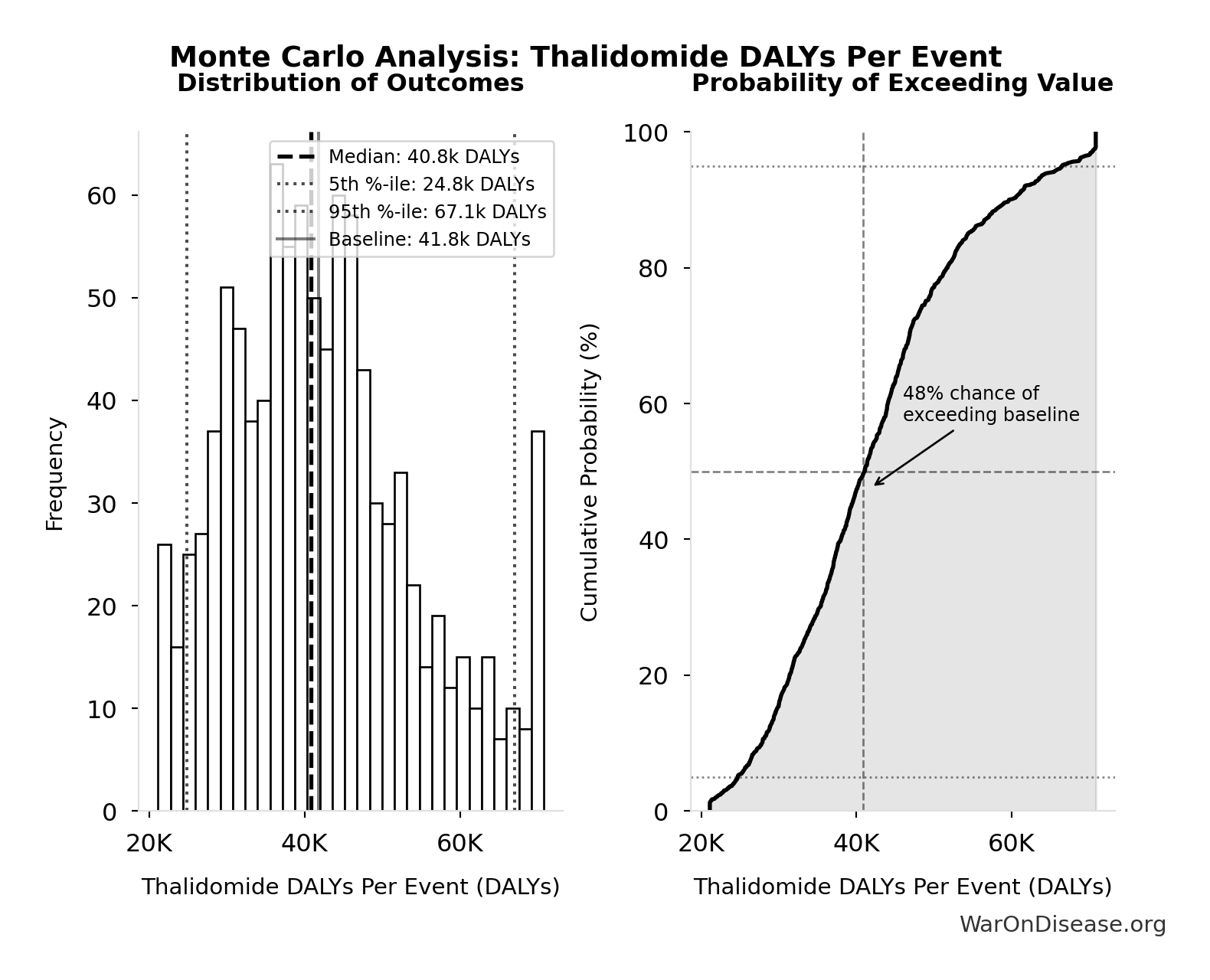
Monte Carlo Distribution
Simulation Results Summary: Thalidomide DALYs Per Event
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 41.8k |
| Mean (expected value) | 42.5k |
| Median (50th percentile) | 40.8k |
| Standard Deviation | 12.2k |
| 90% Confidence Interval | [24.8k, 67.1k] |
The histogram shows the distribution of Thalidomide DALYs Per Event across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
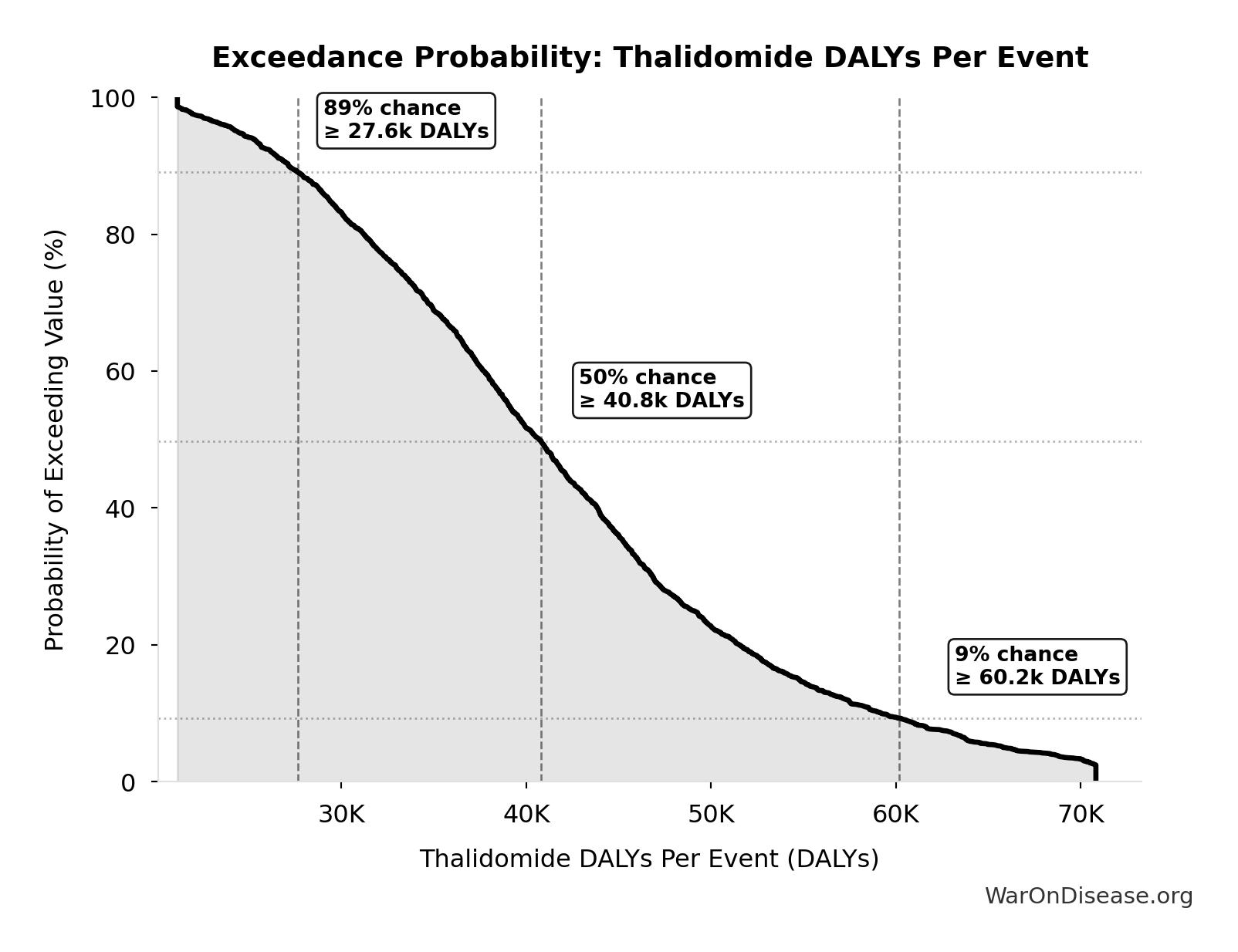
Exceedance Probability
This exceedance probability chart shows the likelihood that Thalidomide DALYs Per Event will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
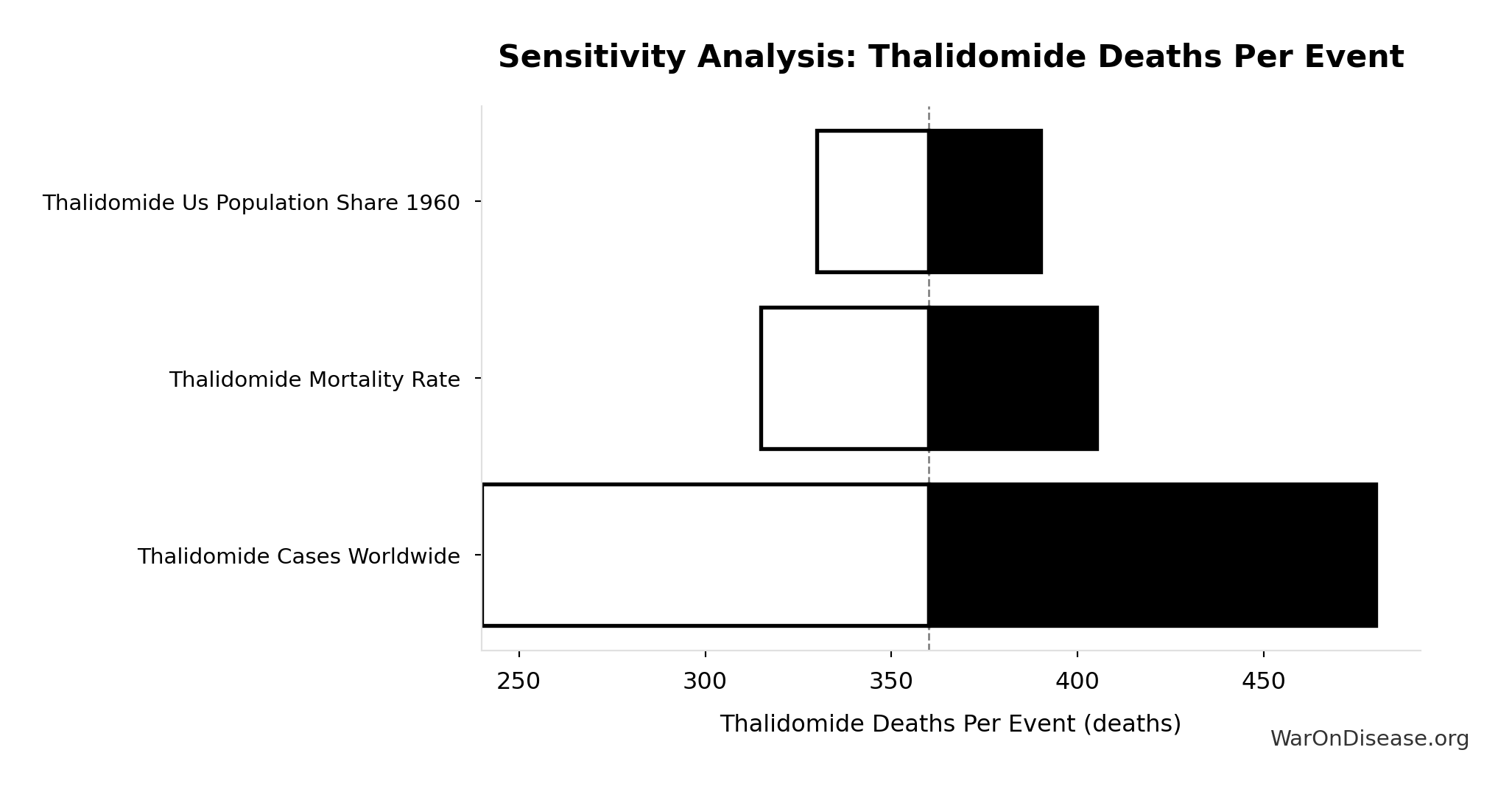
Thalidomide Deaths Per Event: 360 deaths
Noteπ Details
Deaths per US-scale thalidomide event
Inputs:
- Thalidomide Mortality Rate π: 40% (95% CI: 35% - 45%)
- Thalidomide US Cases Prevented π’: 900 cases
\[ \begin{gathered} Deaths_{thal} \\ = Rate_{thal,mort} \times N_{thal,US,prevent} \\ = 40\% \times 900 \\ = 360 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Thalidomide Deaths Per Event
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide US Cases Prevented | 1.5027 | Strong driver |
| Thalidomide Mortality Rate | -0.5048 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
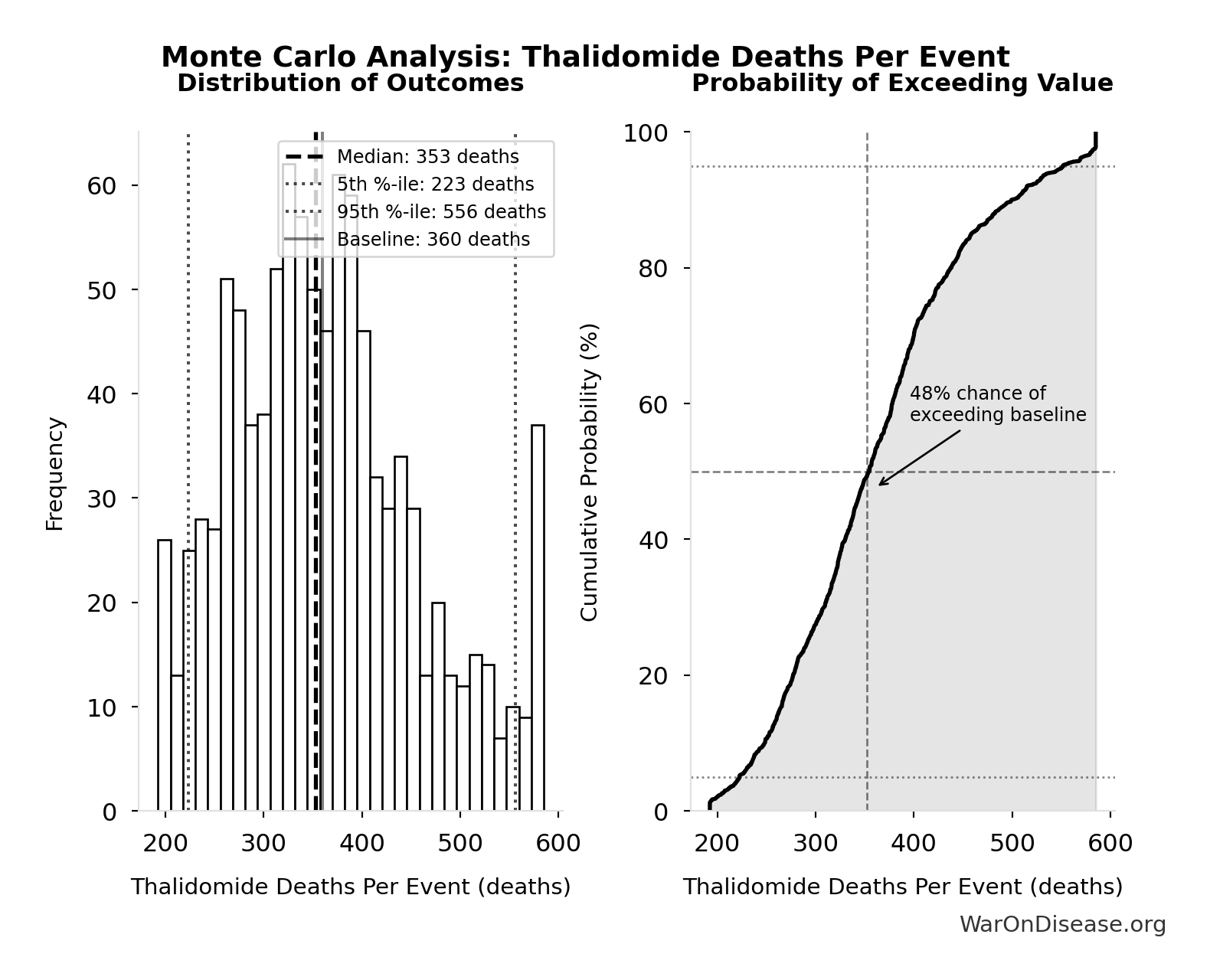
Monte Carlo Distribution
Simulation Results Summary: Thalidomide Deaths Per Event
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 360 |
| Mean (expected value) | 364 |
| Median (50th percentile) | 353 |
| Standard Deviation | 95.8 |
| 90% Confidence Interval | [223, 556] |
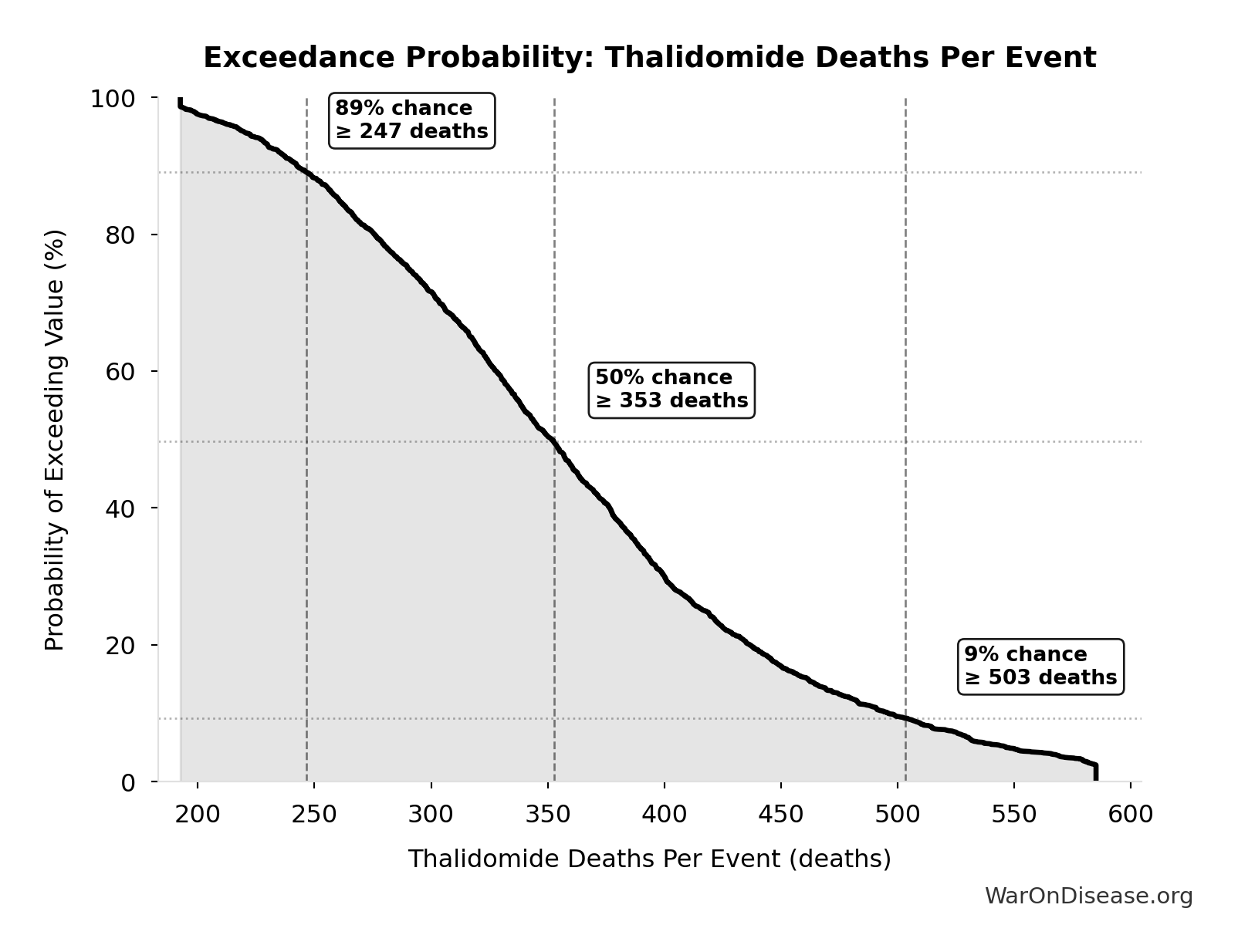
The histogram shows the distribution of Thalidomide Deaths Per Event across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Thalidomide Deaths Per Event will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
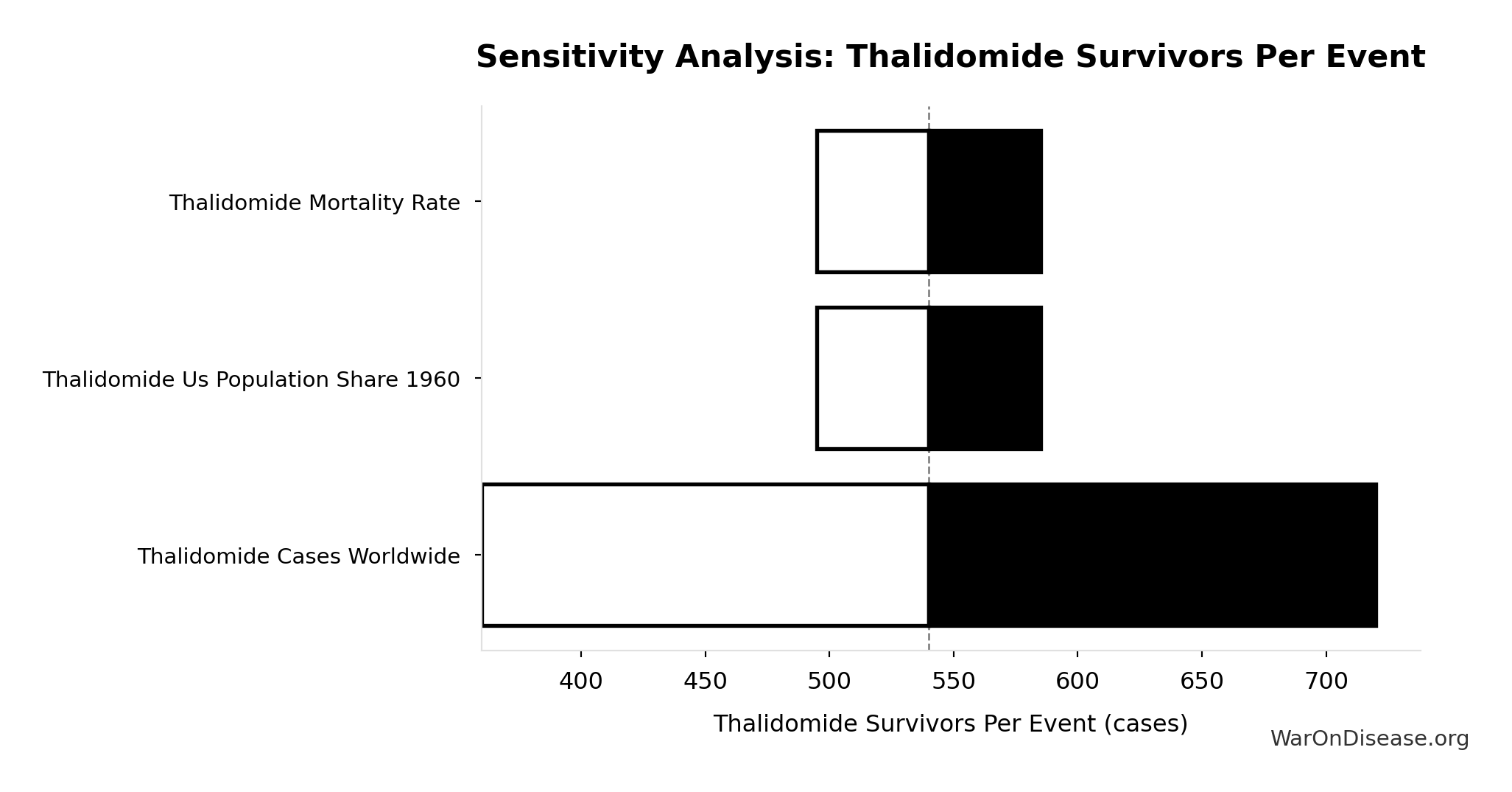
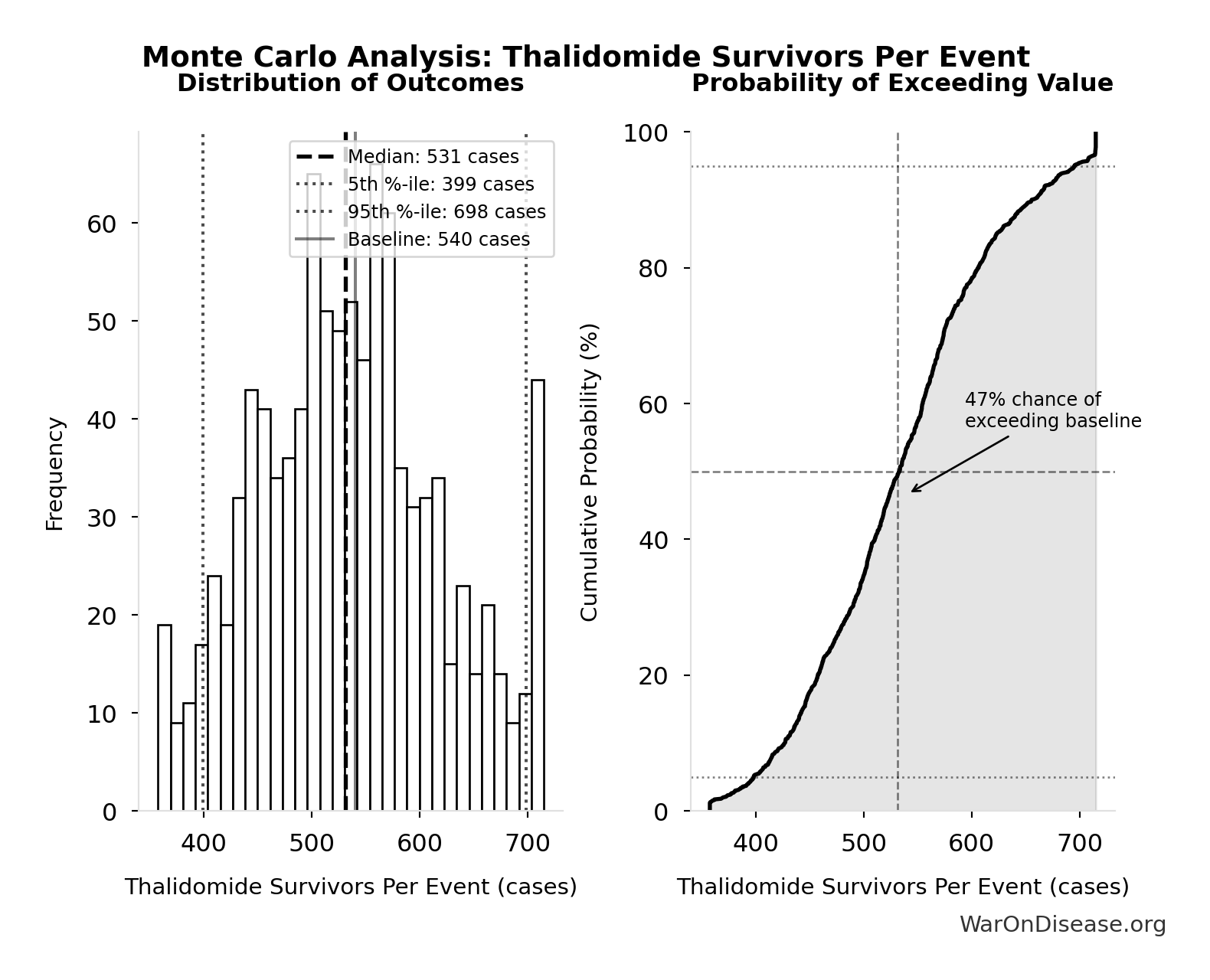
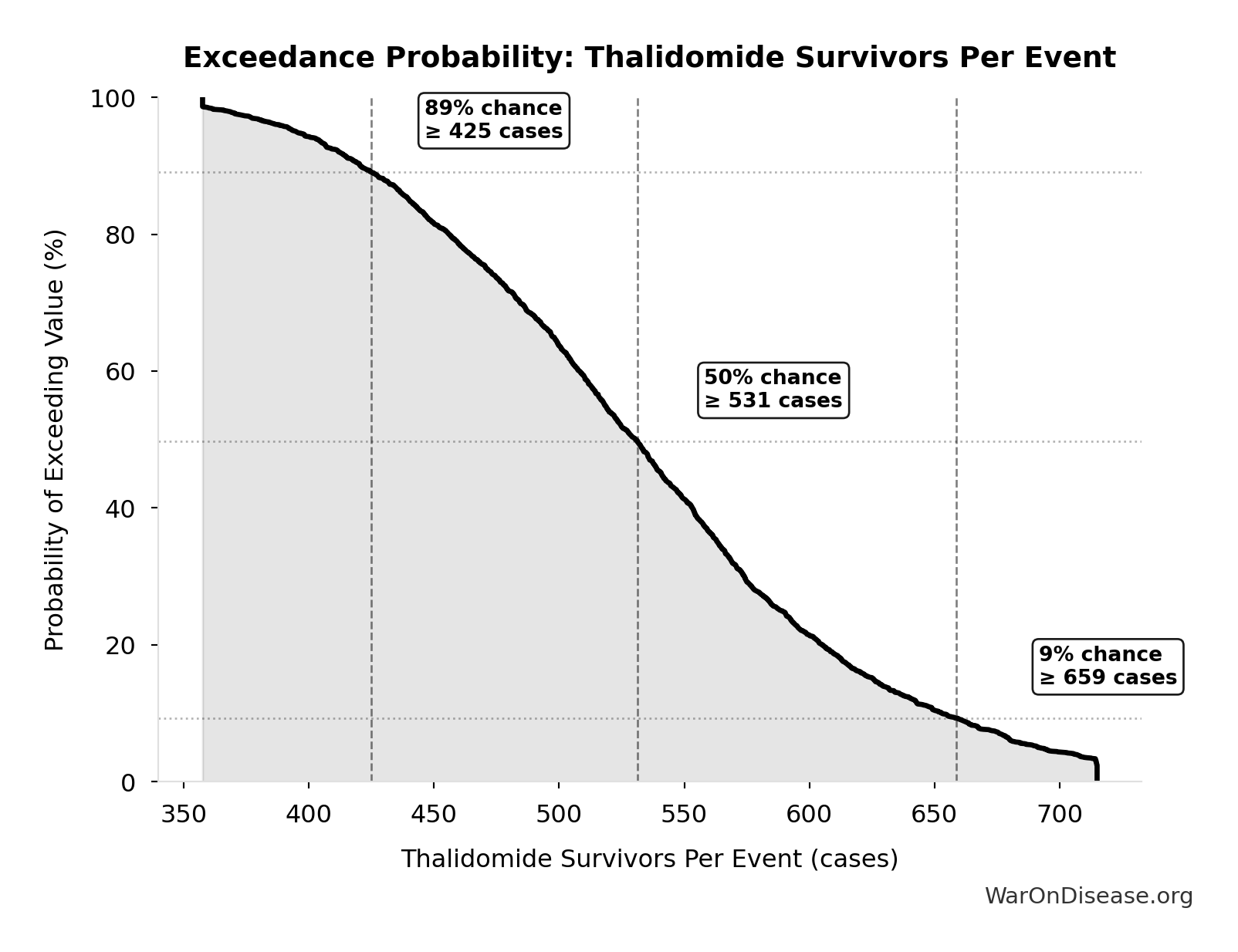
Thalidomide Survivors Per Event: 540 cases
Noteπ Details
Survivors per US-scale thalidomide event
Inputs:
- Thalidomide Mortality Rate π: 40% (95% CI: 35% - 45%)
- Thalidomide US Cases Prevented π’: 900 cases
\[ \begin{gathered} N_{thal,survive} \\ = N_{thal,US,prevent} \times (1 - Rate_{thal,mort}) \\ = 900 \times (1 - 40\%) \\ = 540 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Thalidomide Survivors Per Event
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide Mortality Rate | 0.5607 | Strong driver |
| Thalidomide US Cases Prevented | 0.4398 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Thalidomide Survivors Per Event
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 540 |
| Mean (expected value) | 537 |
| Median (50th percentile) | 531 |
| Standard Deviation | 86.3 |
| 90% Confidence Interval | [399, 698] |
The histogram shows the distribution of Thalidomide Survivors Per Event across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Thalidomide Survivors Per Event will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
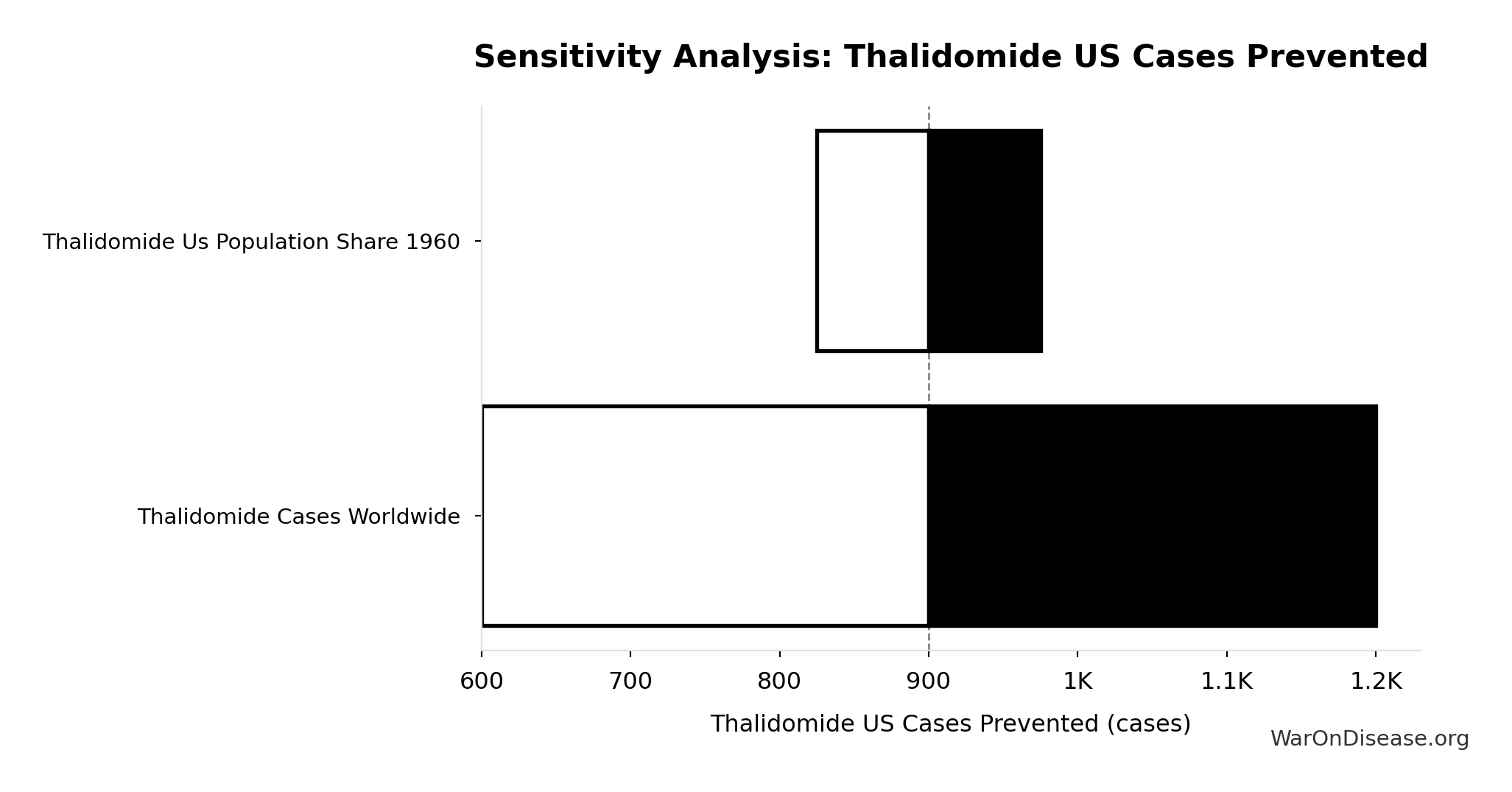
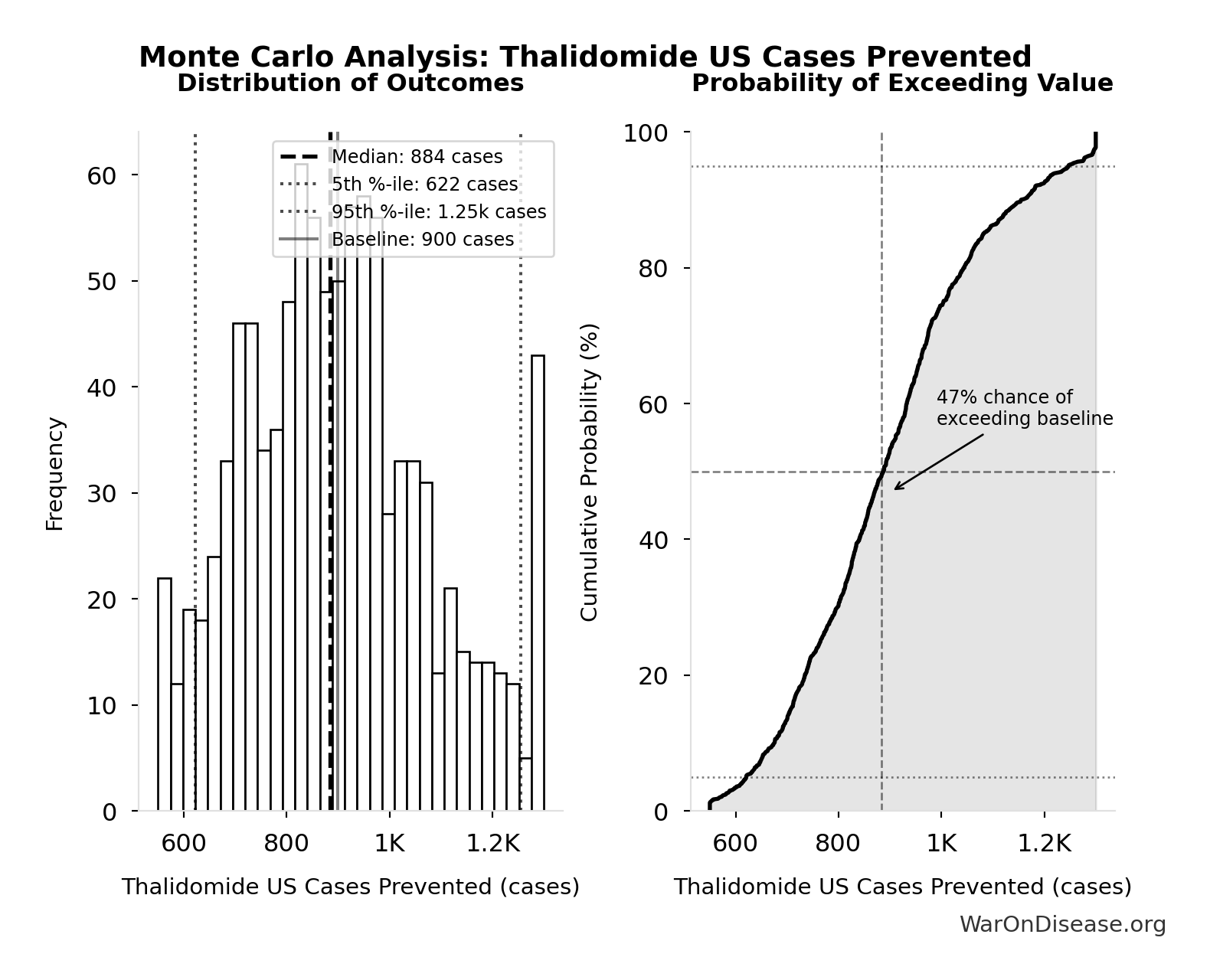
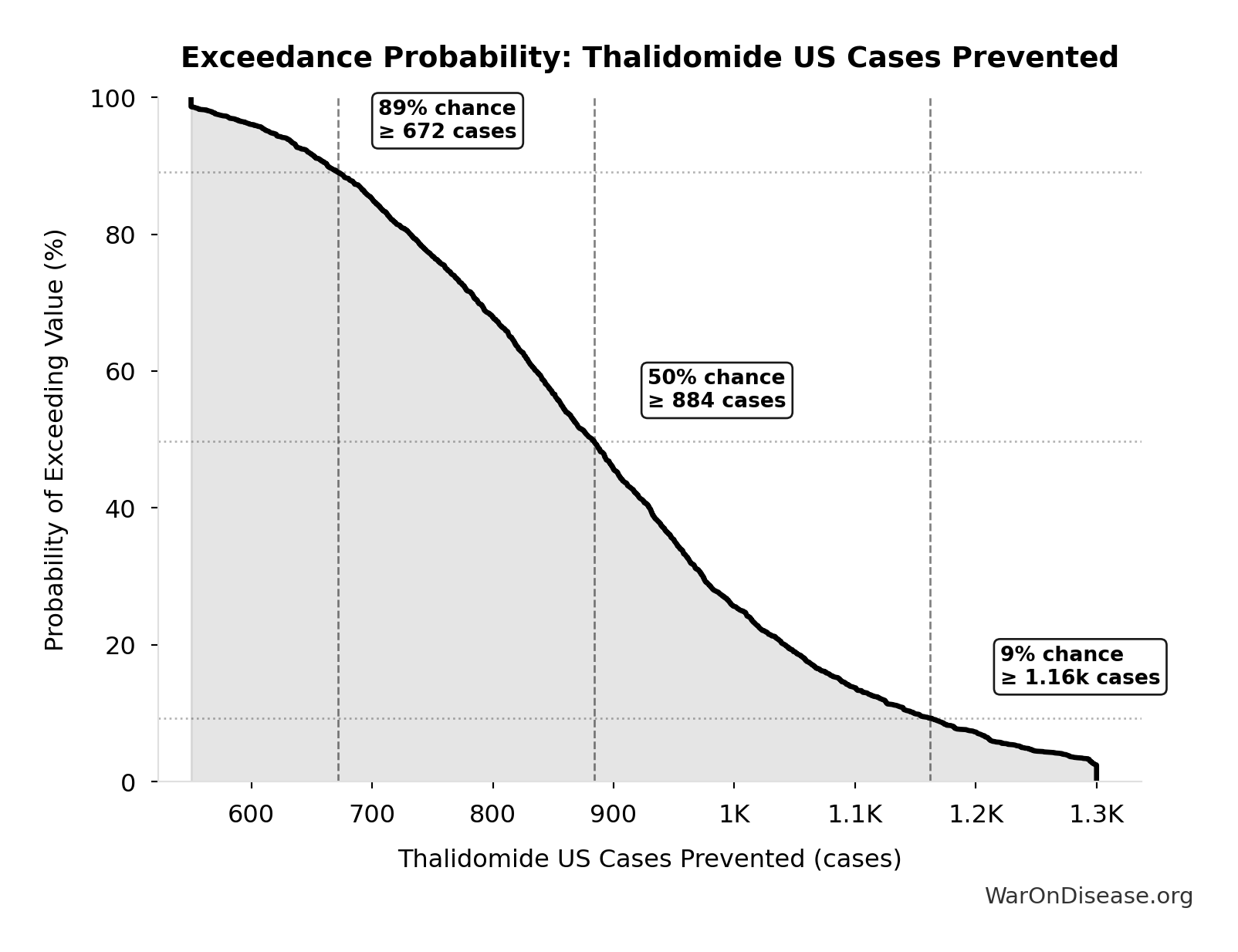
Thalidomide US Cases Prevented: 900 cases
Noteπ Details
Estimated US thalidomide cases prevented by FDA rejection
Inputs:
- Thalidomide Cases Worldwide π: 15.0k cases (95% CI: 10.0k cases - 20.0k cases)
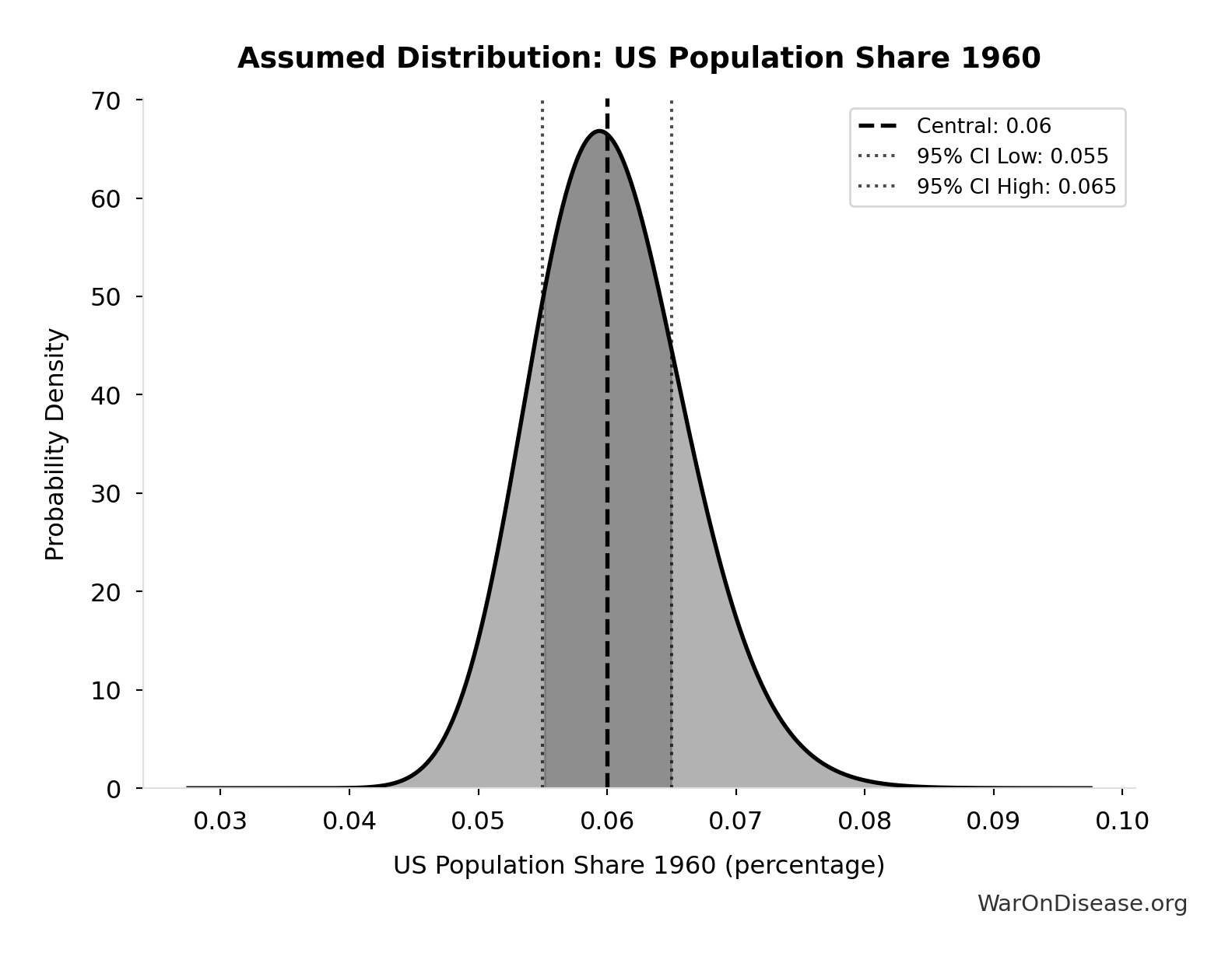
- US Population Share 1960 π: 6% (95% CI: 5.5% - 6.5%)
\[ \begin{gathered} N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Thalidomide US Cases Prevented
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide Cases Worldwide | 1.3746 | Strong driver |
| Thalidomide US Population Share 1960 | -0.3756 | Moderate driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Thalidomide US Cases Prevented
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 900 |
| Mean (expected value) | 901 |
| Median (50th percentile) | 884 |
| Standard Deviation | 182 |
| 90% Confidence Interval | [622, 1.25k] |
The histogram shows the distribution of Thalidomide US Cases Prevented across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Thalidomide US Cases Prevented will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
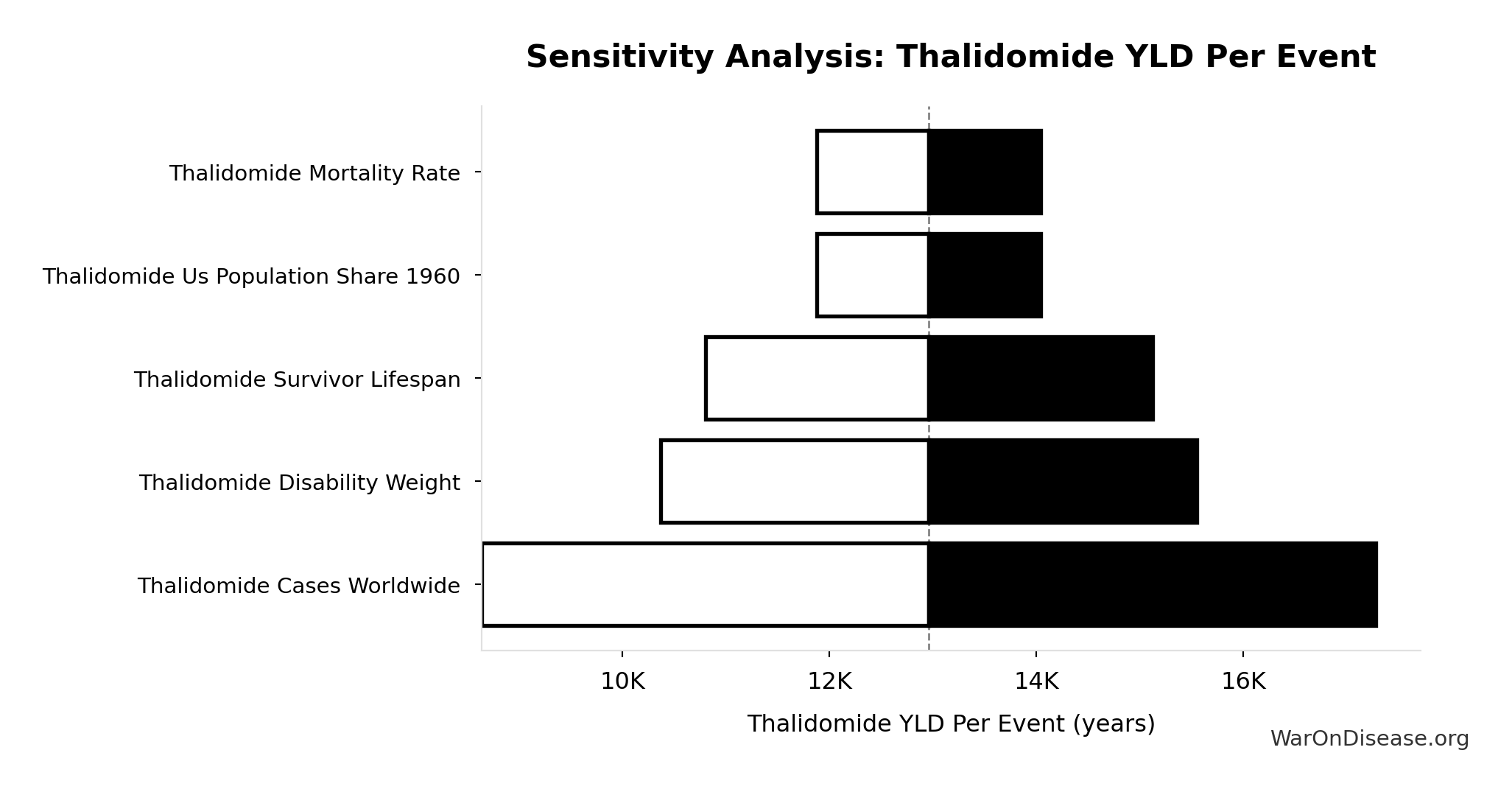
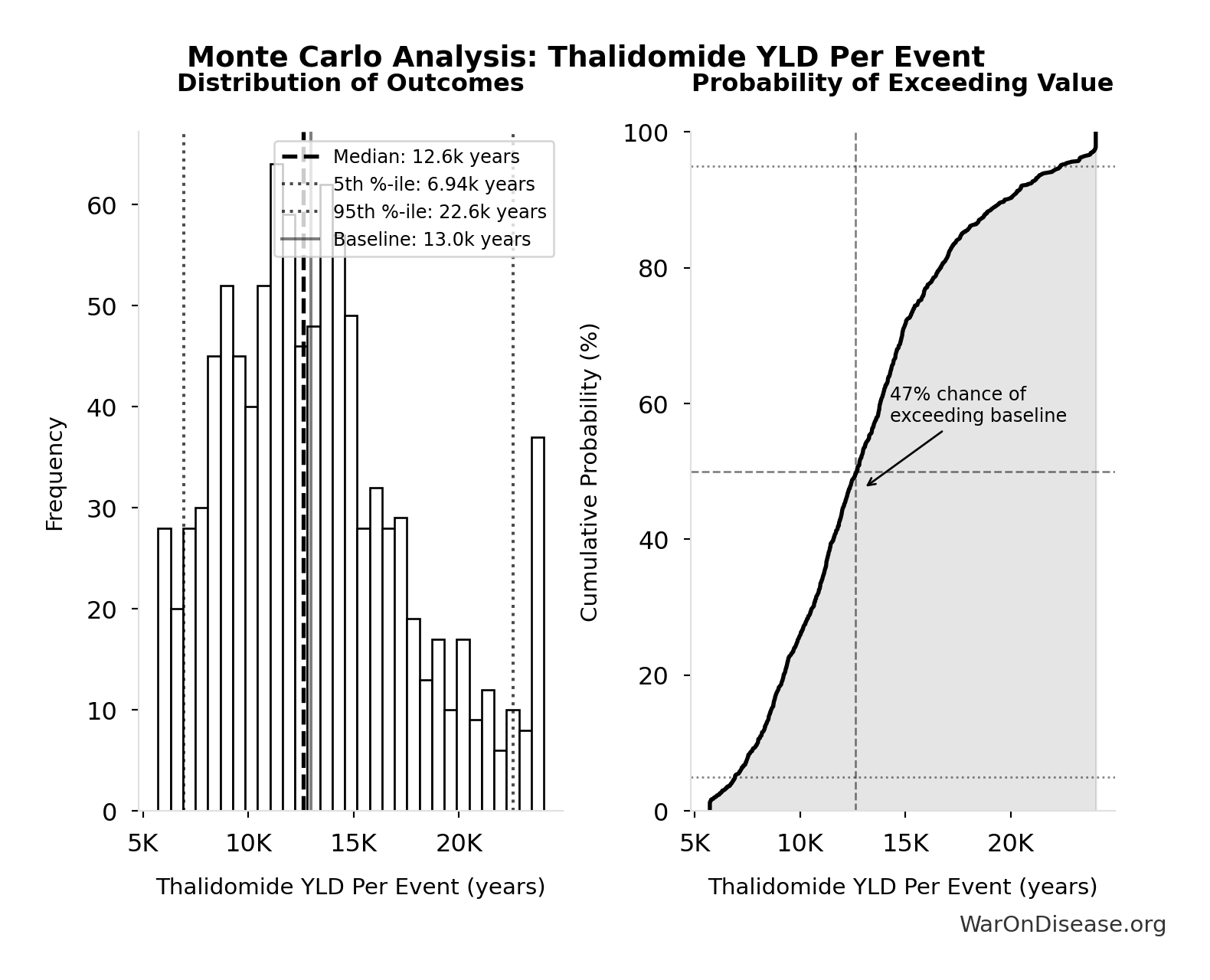
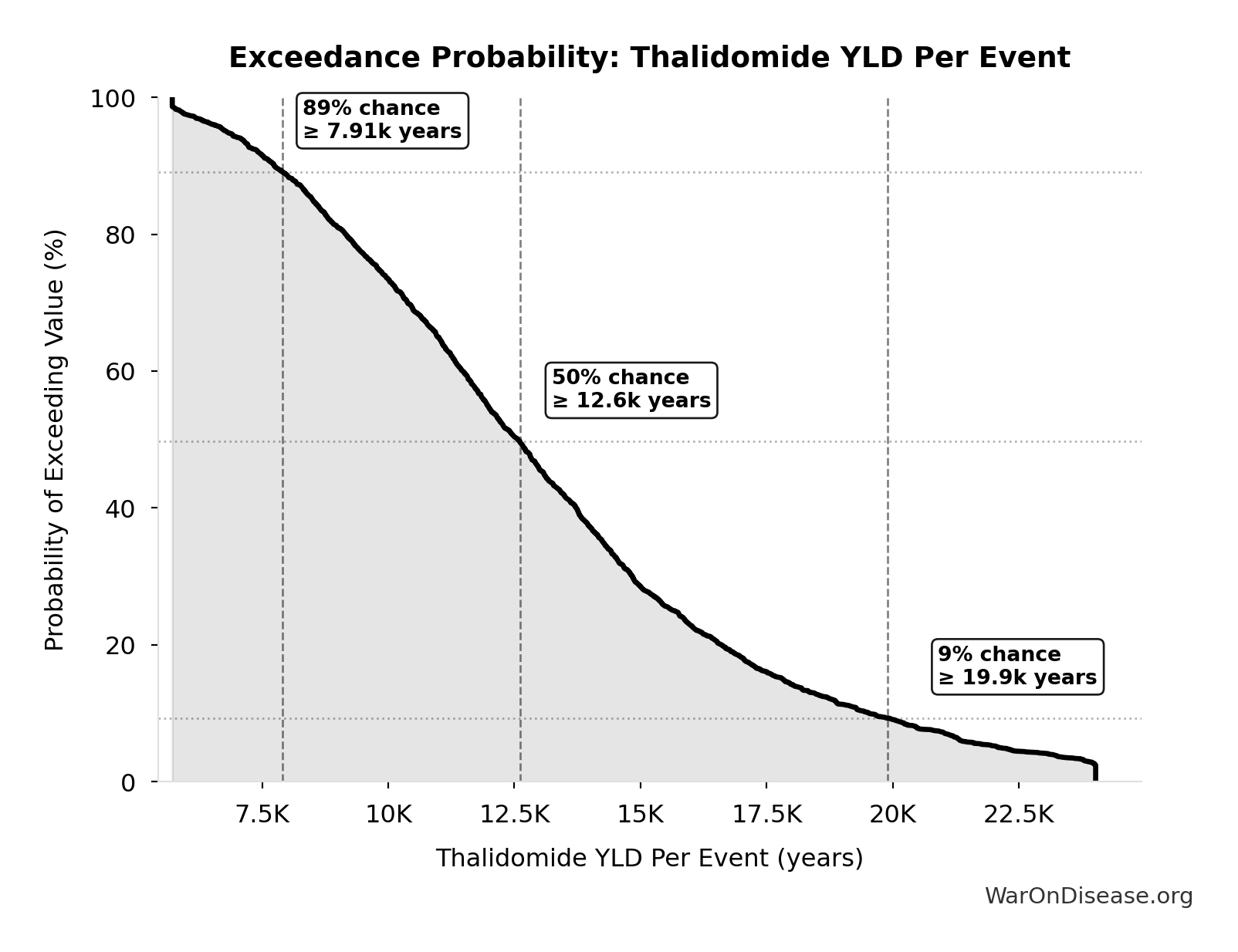
Thalidomide YLD Per Event: 13.0k years
Noteπ Details
Years Lived with Disability per thalidomide event
Inputs:
- Thalidomide Disability Weight π: 0.4:1 (95% CI: 0.32:1 - 0.48:1)
- Thalidomide Survivors Per Event π’: 540 cases
- Thalidomide Survivor Lifespan π: 60 years (95% CI: 50 years - 70 years)
\[ \begin{gathered} YLD_{thal} \\ = DW_{thal} \times N_{thal,survive} \times LE_{thal} \\ = 0.4 \times 540 \times 60 \\ = 13{,}000 \\[0.5em] \text{where } N_{thal,survive} \\ = N_{thal,US,prevent} \times (1 - Rate_{thal,mort}) \\ = 900 \times (1 - 40\%) \\ = 540 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Thalidomide YLD Per Event
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide Disability Weight | 28.4785 | Strong driver |
| Thalidomide Survivor Lifespan | -23.4440 | Strong driver |
| Thalidomide Survivors Per Event | -4.0444 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Thalidomide YLD Per Event
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 13.0k |
| Mean (expected value) | 13.3k |
| Median (50th percentile) | 12.6k |
| Standard Deviation | 4.50k |
| 90% Confidence Interval | [6.94k, 22.6k] |
The histogram shows the distribution of Thalidomide YLD Per Event across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Thalidomide YLD Per Event will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
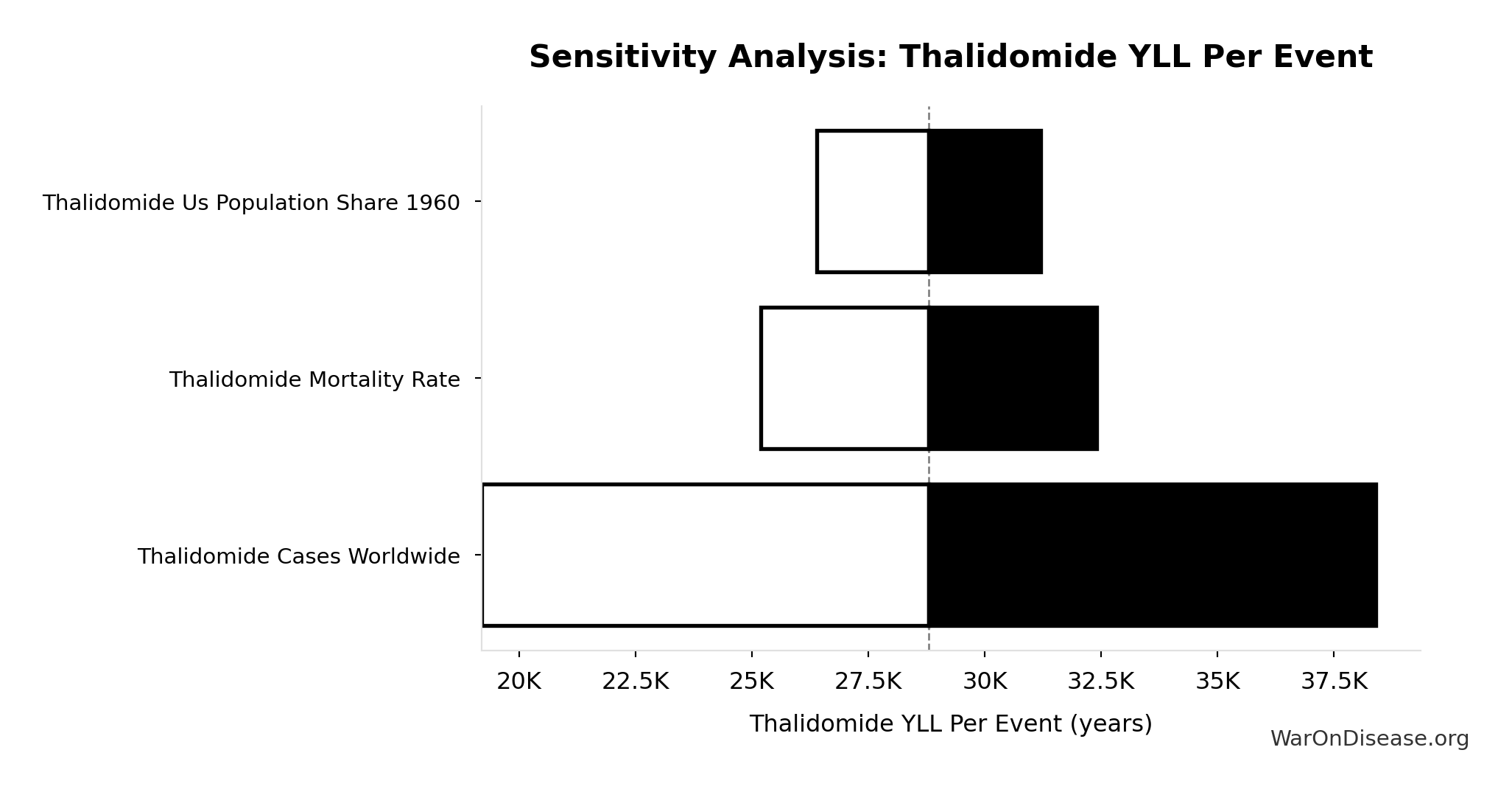
Thalidomide YLL Per Event: 28.8k years
Noteπ Details
Years of Life Lost per thalidomide event (infant deaths)
Inputs:
- Thalidomide Deaths Per Event π’: 360 deaths
\[ \begin{gathered} YLL_{thal} = Deaths_{thal} \times 80 = 360 \times 80 = 28{,}800 \\[0.5em] \text{where } Deaths_{thal} \\ = Rate_{thal,mort} \times N_{thal,US,prevent} \\ = 40\% \times 900 \\ = 360 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Thalidomide YLL Per Event
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide Deaths Per Event | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
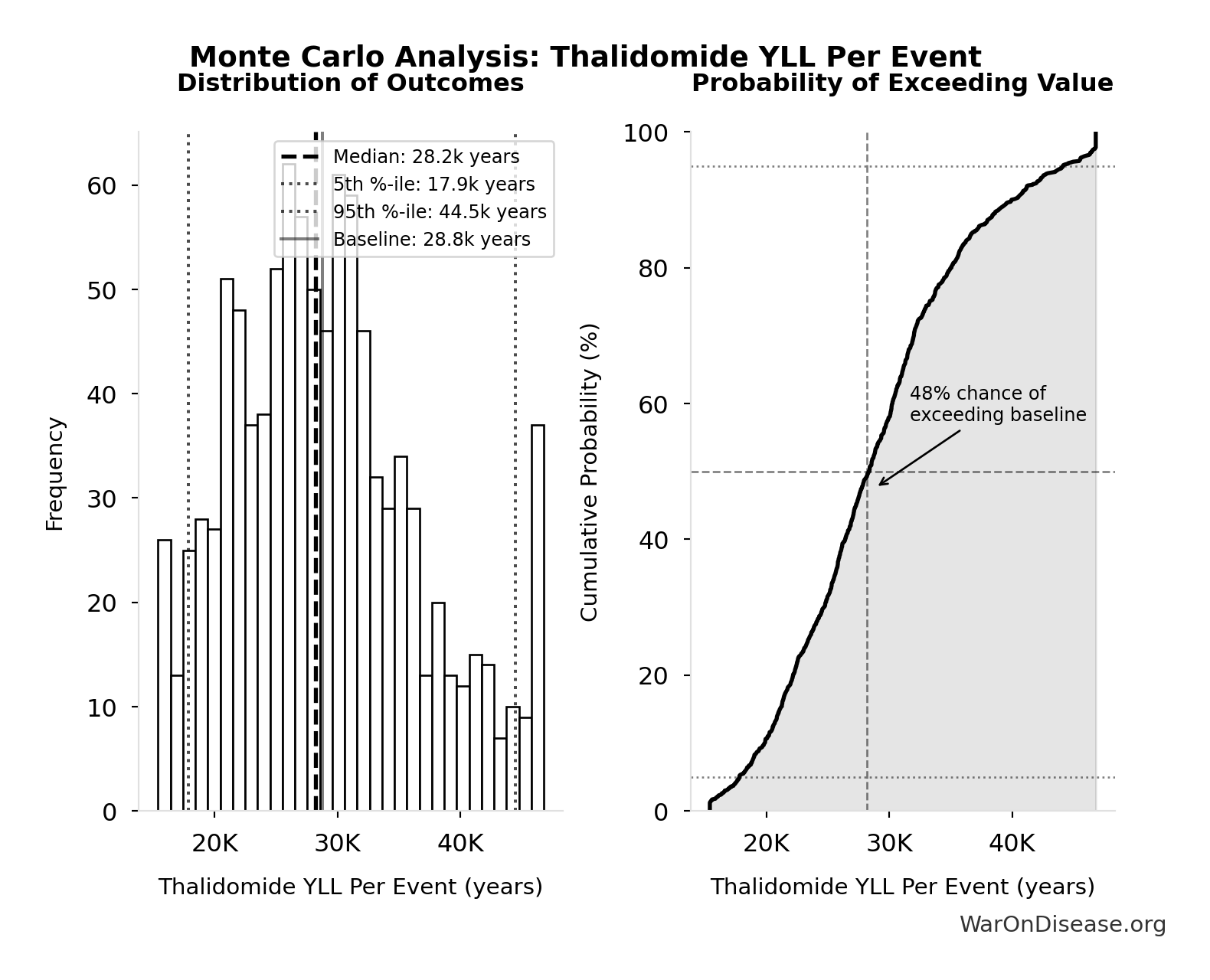
Monte Carlo Distribution
Simulation Results Summary: Thalidomide YLL Per Event
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 28.8k |
| Mean (expected value) | 29.2k |
| Median (50th percentile) | 28.2k |
| Standard Deviation | 7.67k |
| 90% Confidence Interval | [17.9k, 44.5k] |
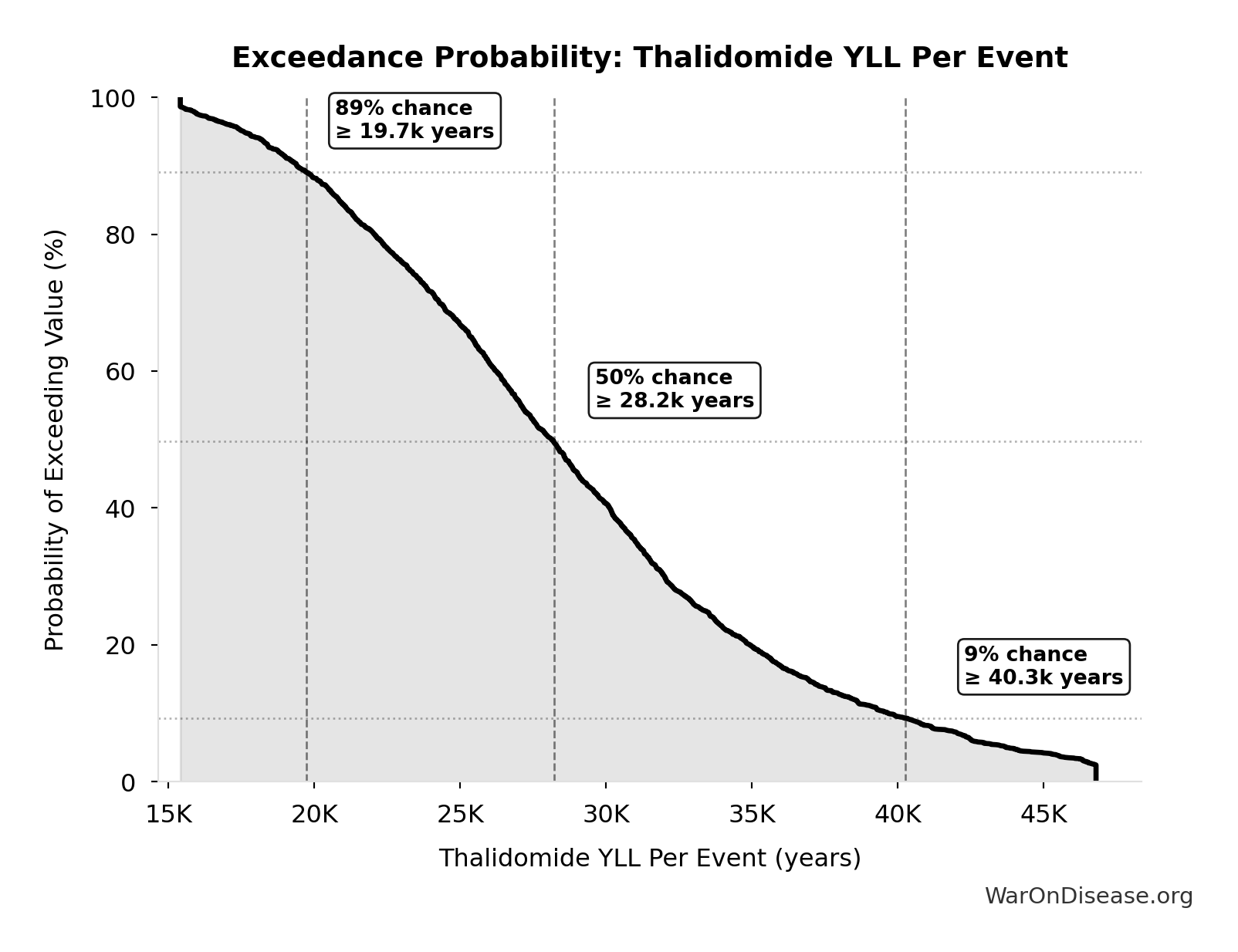
The histogram shows the distribution of Thalidomide YLL Per Event across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Thalidomide YLL Per Event will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
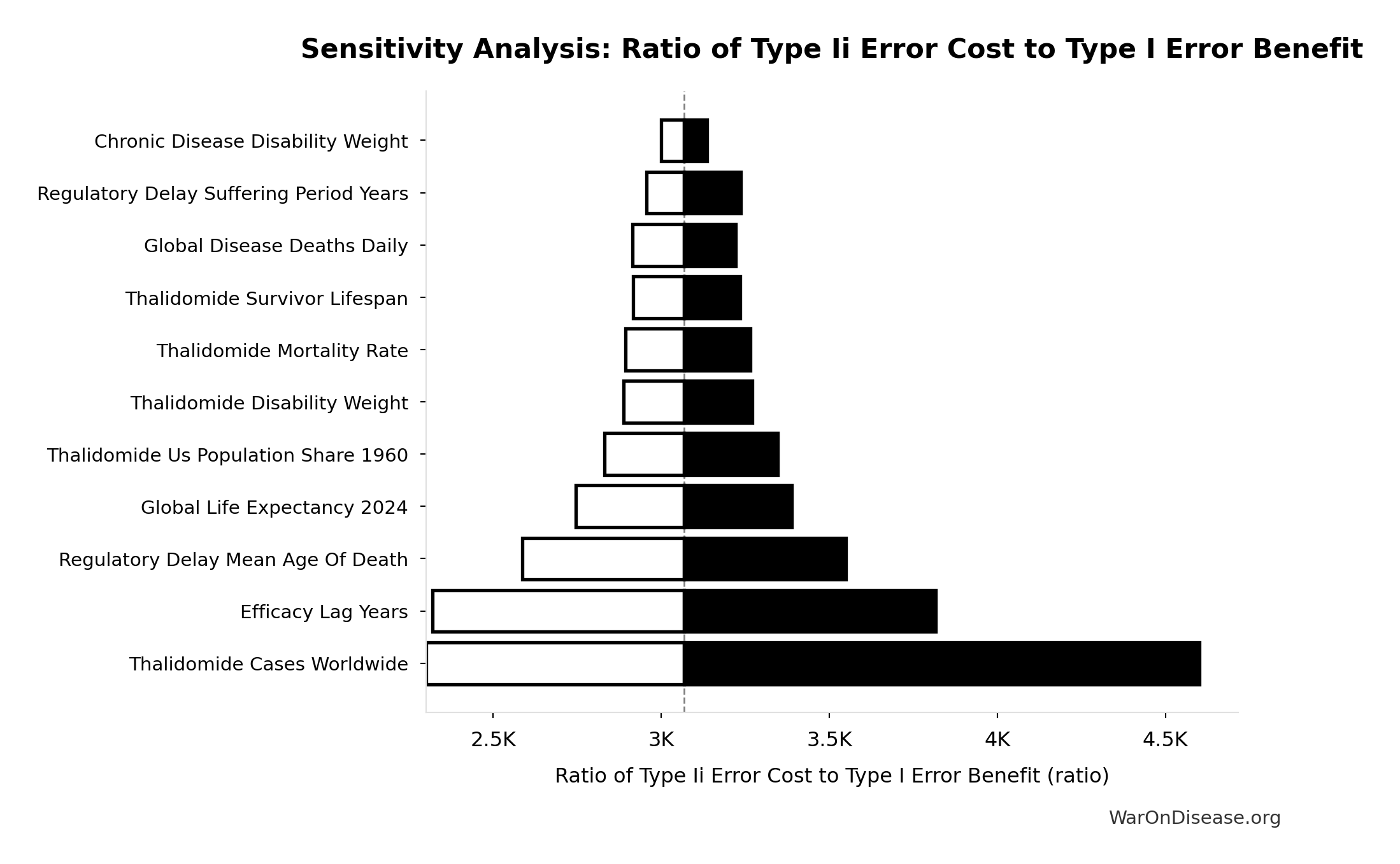
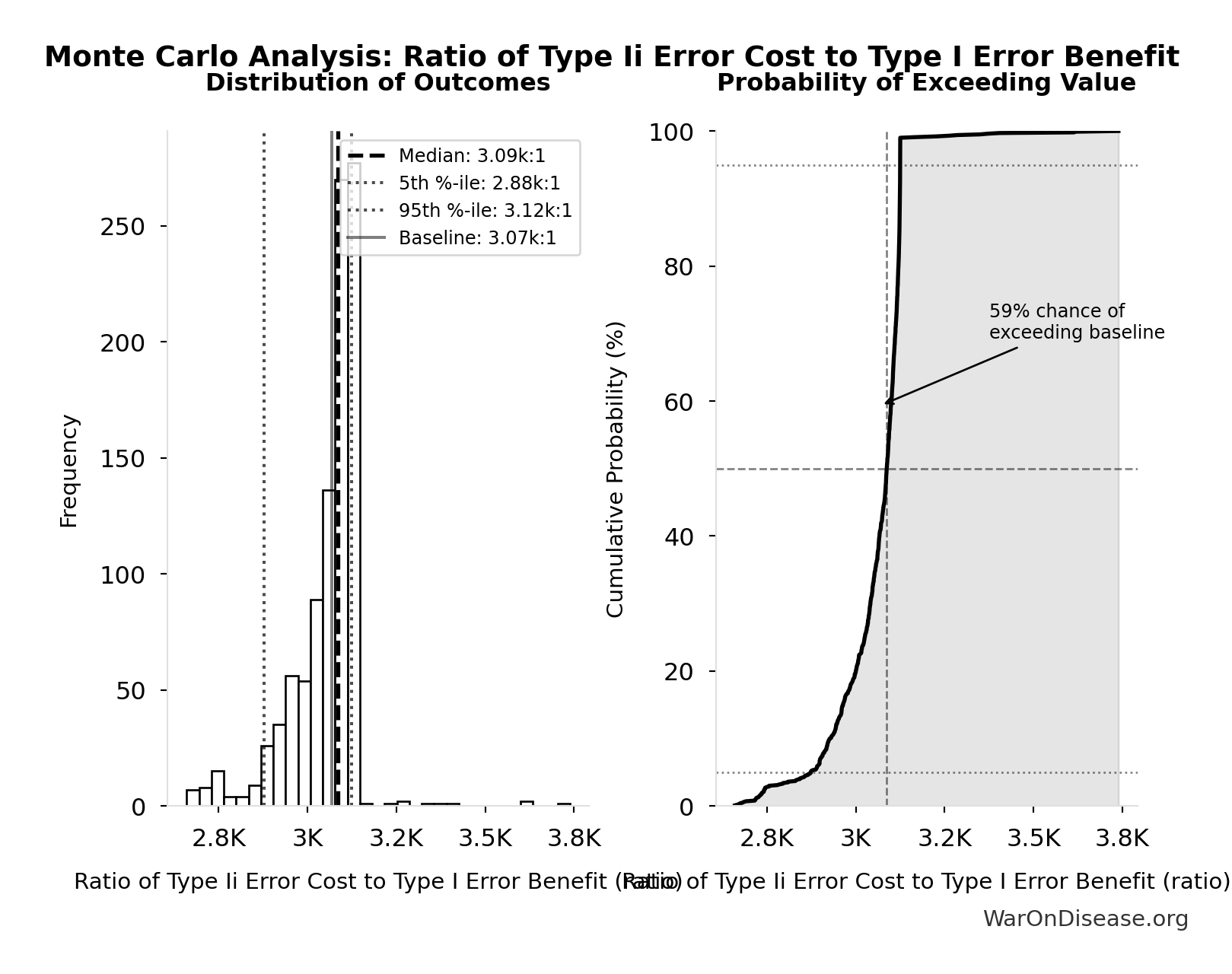
Ratio of Type Ii Error Cost to Type I Error Benefit: 3.07k:1
Noteπ Details
Ratio of Type II error cost to Type I error benefit (harm from delay vs. harm prevented)
Inputs:
- Total DALYs Lost from Disease Eradication Delay π’: 7.94B DALYs
- Maximum DALYs Saved by FDA Preventing Unsafe Drugs (1962-2024) π’: 2.59M DALYs
\[ \begin{gathered} Ratio_{TypeII} = \frac{DALYs_{lag}}{DALY_{TypeI}} = \frac{7.94B}{2.59M} = 3{,}070 \\[0.5em] \text{where } DALYs_{lag} = YLL_{lag} + YLD_{lag} = 7.07B + 873M = 7.94B \\[0.5em] \text{where } YLL_{lag} \\ = Deaths_{lag} \times (LE_{global} - Age_{death,delay}) \\ = 416M \times (79 - 62) \\ = 7.07B \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \\[0.5em] \text{where } YLD_{lag} \\ = Deaths_{lag} \times T_{suffering} \times DW_{chronic} \\ = 416M \times 6 \times 0.35 \\ = 873M \\[0.5em] \text{where } Deaths_{lag} \\ = T_{lag} \times Deaths_{disease,daily} \times 338 \\ = 8.2 \times 150{,}000 \times 338 \\ = 416M \\[0.5em] \text{where } DALY_{TypeI} = DALY_{thal} \times 62 = 41{,}800 \times 62 = 2.59M \\[0.5em] \text{where } DALY_{thal} \\ = YLD_{thal} + YLL_{thal} \\ = 13{,}000 + 28{,}800 \\ = 41{,}800 \\[0.5em] \text{where } YLD_{thal} \\ = DW_{thal} \times N_{thal,survive} \times LE_{thal} \\ = 0.4 \times 540 \times 60 \\ = 13{,}000 \\[0.5em] \text{where } N_{thal,survive} \\ = N_{thal,US,prevent} \times (1 - Rate_{thal,mort}) \\ = 900 \times (1 - 40\%) \\ = 540 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \\[0.5em] \text{where } YLL_{thal} = Deaths_{thal} \times 80 = 360 \times 80 = 28{,}800 \\[0.5em] \text{where } Deaths_{thal} \\ = Rate_{thal,mort} \times N_{thal,US,prevent} \\ = 40\% \times 900 \\ = 360 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#risk-analysis
~ Medium confidence
Sensitivity Analysis
Sensitivity Indices for Ratio of Type Ii Error Cost to Type I Error Benefit
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| dFDA Efficacy Lag Elimination DALYs | 7.2872 | Strong driver |
| Type I Error Benefit DALYs | -7.1207 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Ratio of Type Ii Error Cost to Type I Error Benefit
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 3.07k:1 |
| Mean (expected value) | 3.05k:1 |
| Median (50th percentile) | 3.09k:1 |
| Standard Deviation | 101:1 |
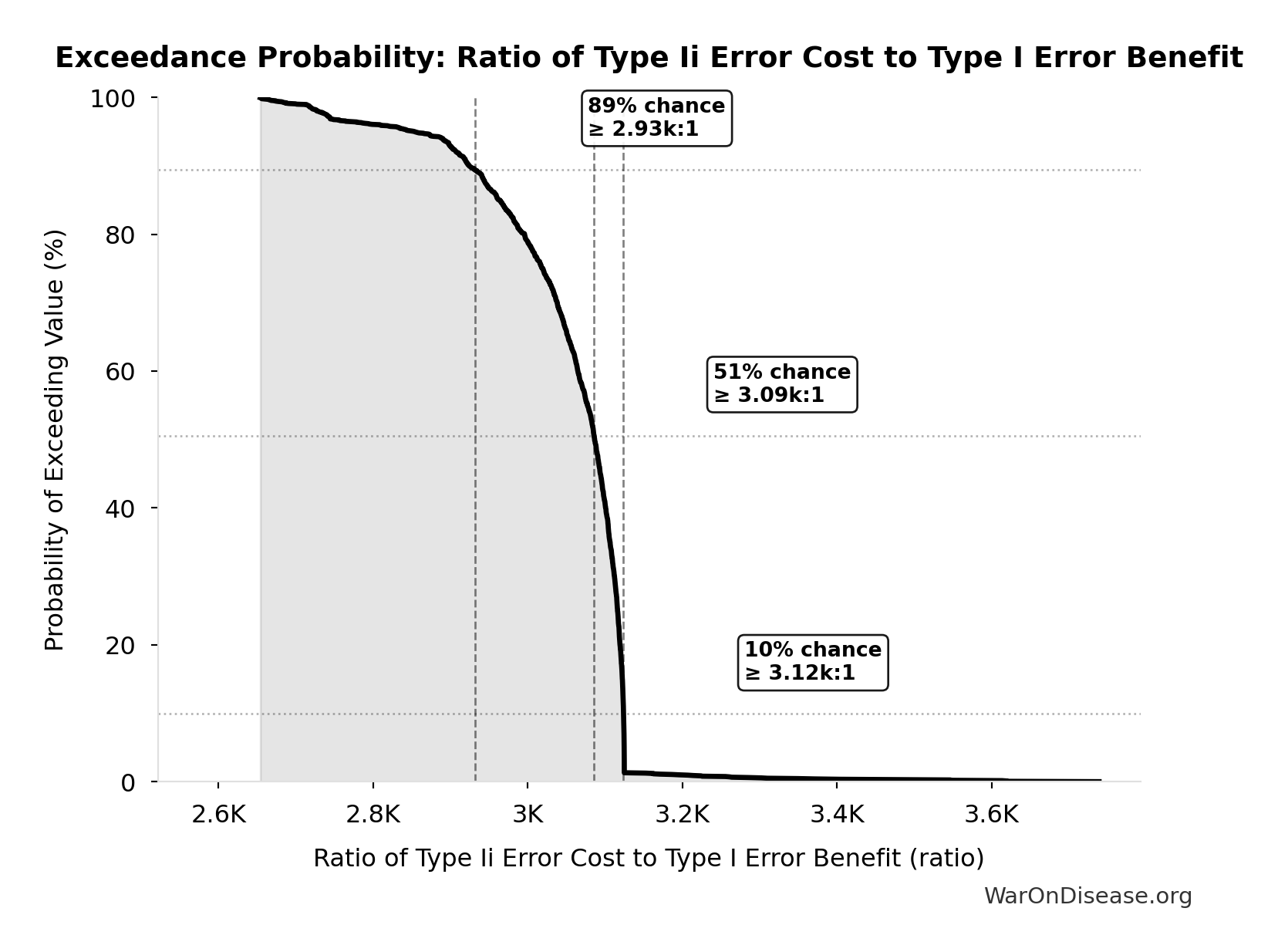
| 90% Confidence Interval | [2.88k:1, 3.12k:1] |
The histogram shows the distribution of Ratio of Type Ii Error Cost to Type I Error Benefit across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Ratio of Type Ii Error Cost to Type I Error Benefit will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
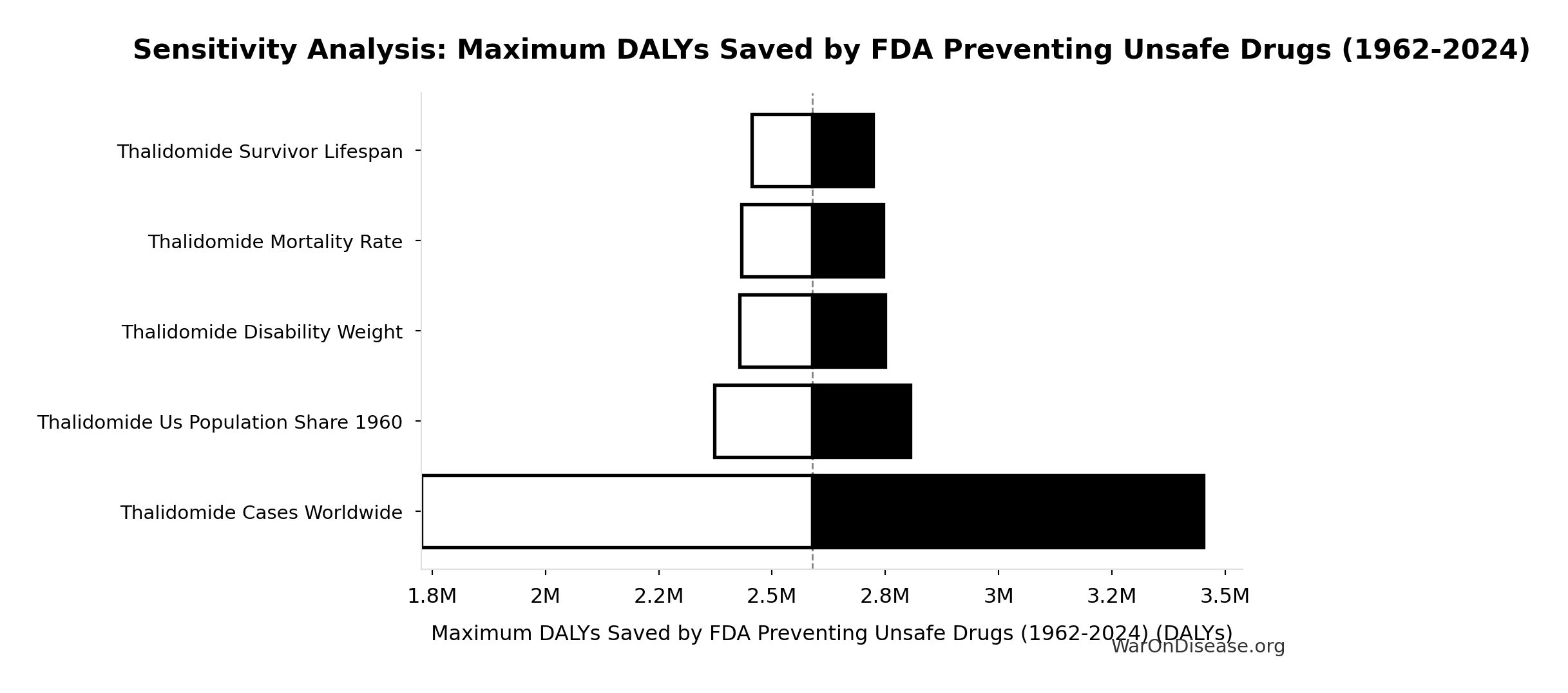
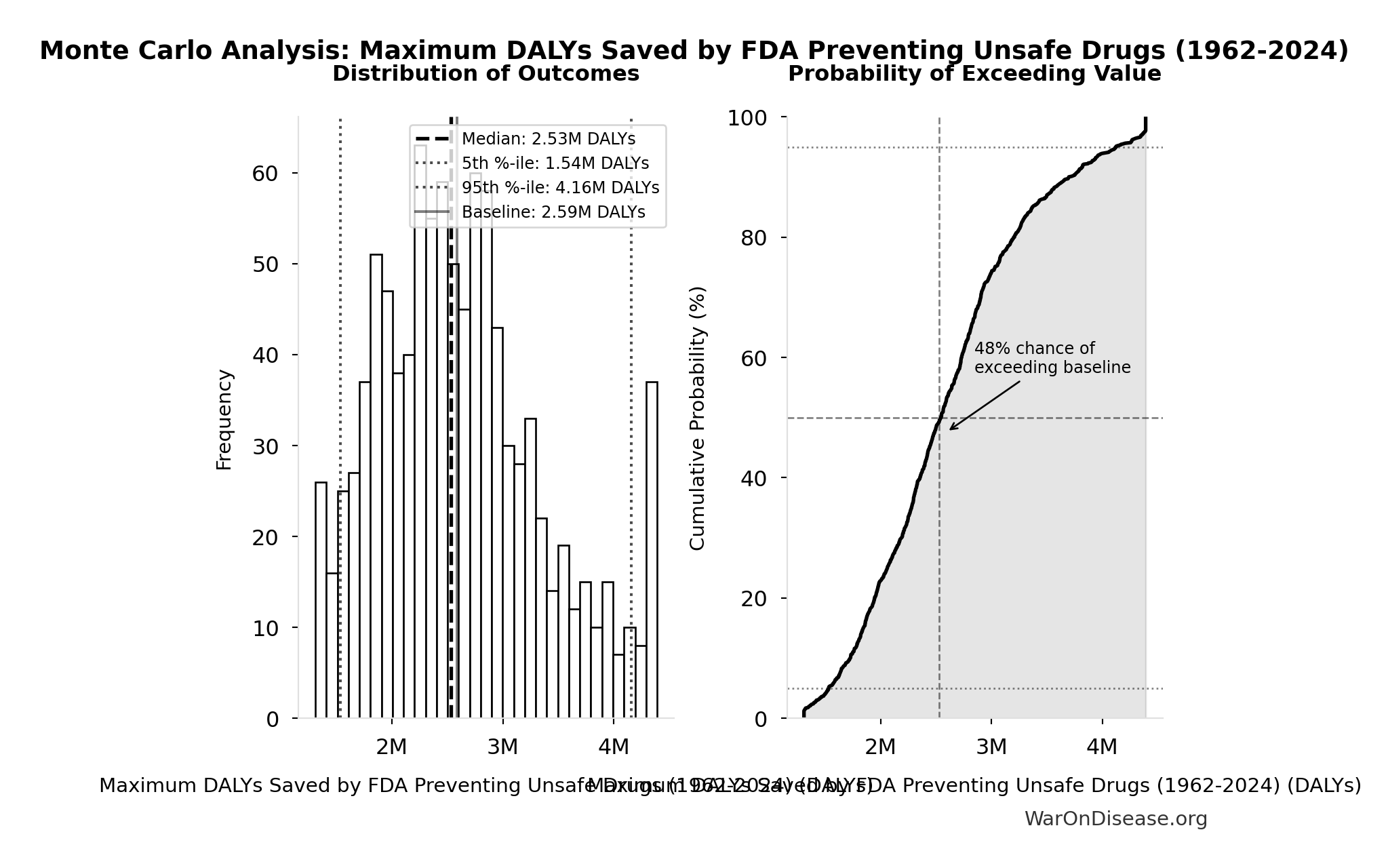
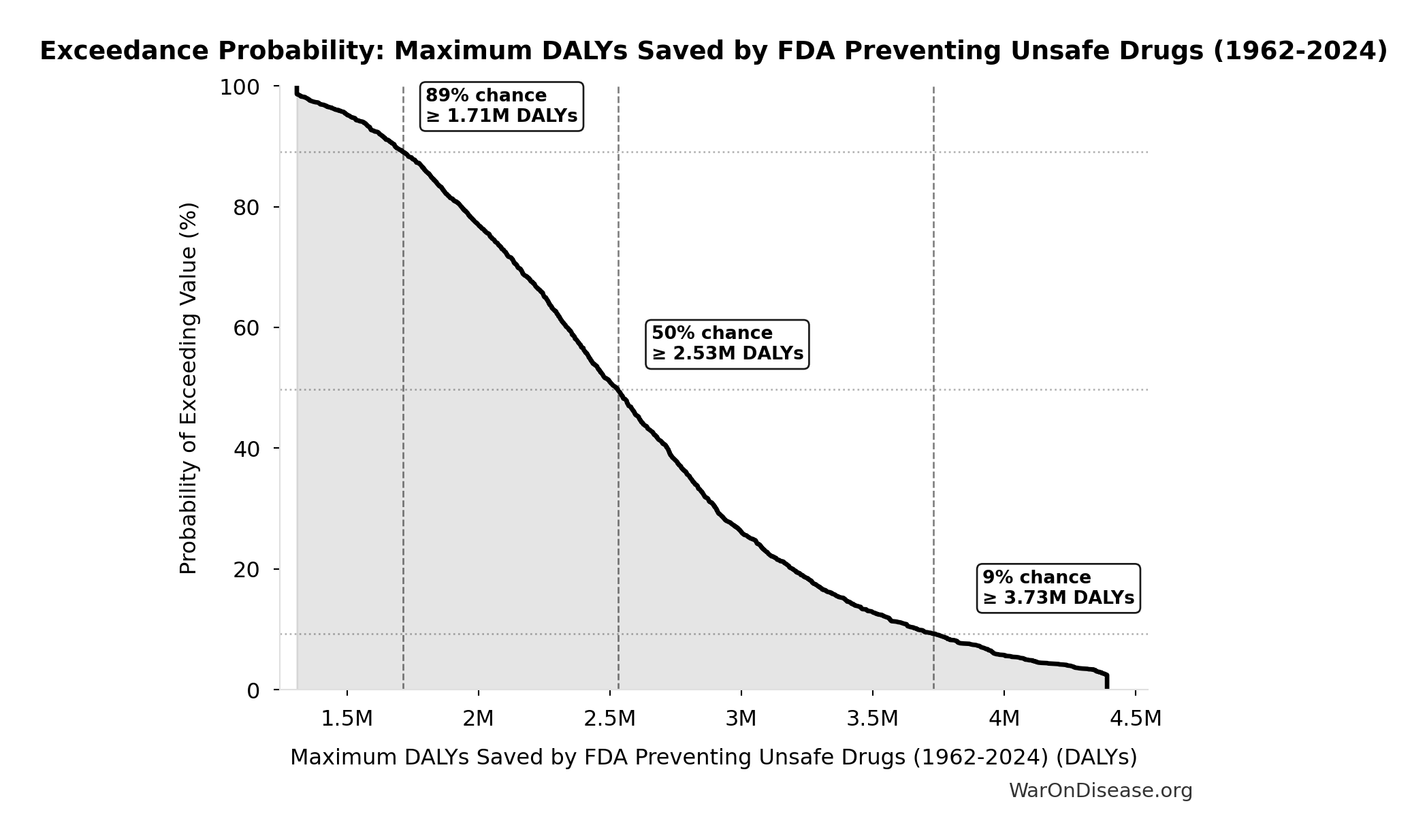
Maximum DALYs Saved by FDA Preventing Unsafe Drugs (1962-2024): 2.59M DALYs
Noteπ Details
Maximum DALYs saved by FDA preventing unsafe drugs over 62-year period 1962-2024 (extreme overestimate: one Thalidomide-scale event per year)
Inputs:
- Thalidomide DALYs Per Event π’: 41.8k DALYs
\[ \begin{gathered} DALY_{TypeI} = DALY_{thal} \times 62 = 41{,}800 \times 62 = 2.59M \\[0.5em] \text{where } DALY_{thal} \\ = YLD_{thal} + YLL_{thal} \\ = 13{,}000 + 28{,}800 \\ = 41{,}800 \\[0.5em] \text{where } YLD_{thal} \\ = DW_{thal} \times N_{thal,survive} \times LE_{thal} \\ = 0.4 \times 540 \times 60 \\ = 13{,}000 \\[0.5em] \text{where } N_{thal,survive} \\ = N_{thal,US,prevent} \times (1 - Rate_{thal,mort}) \\ = 900 \times (1 - 40\%) \\ = 540 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \\[0.5em] \text{where } YLL_{thal} = Deaths_{thal} \times 80 = 360 \times 80 = 28{,}800 \\[0.5em] \text{where } Deaths_{thal} \\ = Rate_{thal,mort} \times N_{thal,US,prevent} \\ = 40\% \times 900 \\ = 360 \\[0.5em] \text{where } N_{thal,US,prevent} \\ = N_{thal,global} \times Pct_{US,1960} \\ = 15{,}000 \times 6\% \\ = 900 \end{gathered} \]
Methodology: ../appendix/invisible-graveyard#risk-analysis
? Low confidence
Sensitivity Analysis
Sensitivity Indices for Maximum DALYs Saved by FDA Preventing Unsafe Drugs (1962-2024)
Regression-based sensitivity showing which inputs explain the most variance in the output.
| Input Parameter | Sensitivity Coefficient | Interpretation |
|---|---|---|
| Thalidomide DALYs Per Event | 1.0000 | Strong driver |
Interpretation: Standardized coefficients show the change in output (in SD units) per 1 SD change in input. Values near Β±1 indicate strong influence; values exceeding Β±1 may occur with correlated inputs.
Monte Carlo Distribution
Simulation Results Summary: Maximum DALYs Saved by FDA Preventing Unsafe Drugs (1962-2024)
| Statistic | Value |
|---|---|
| Baseline (deterministic) | 2.59M |
| Mean (expected value) | 2.63M |
| Median (50th percentile) | 2.53M |
| Standard Deviation | 754k |
| 90% Confidence Interval | [1.54M, 4.16M] |
The histogram shows the distribution of Maximum DALYs Saved by FDA Preventing Unsafe Drugs (1962-2024) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Exceedance Probability
This exceedance probability chart shows the likelihood that Maximum DALYs Saved by FDA Preventing Unsafe Drugs (1962-2024) will exceed any given threshold. Higher curves indicate more favorable outcomes with greater certainty.
External Data Sources
Parameters sourced from peer-reviewed publications, institutional databases, and authoritative reports.
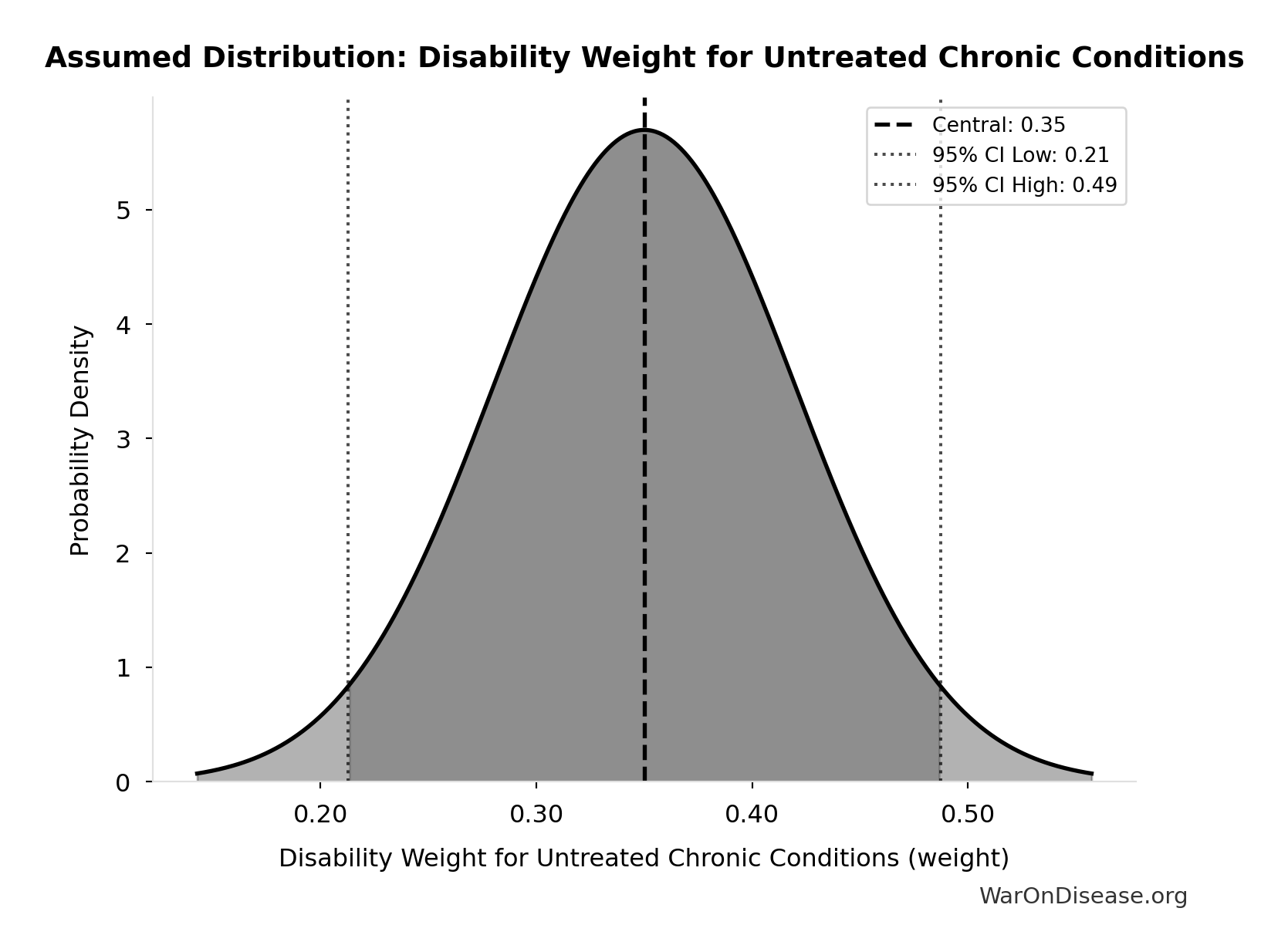
Disability Weight for Untreated Chronic Conditions: 0.35 weight
Noteπ Details
Disability weight for untreated chronic conditions (WHO Global Burden of Disease)
Source:18
Uncertainty Range
Technical: Distribution: Normal (SE: 0.07 weight)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence β’ π Peer-reviewed
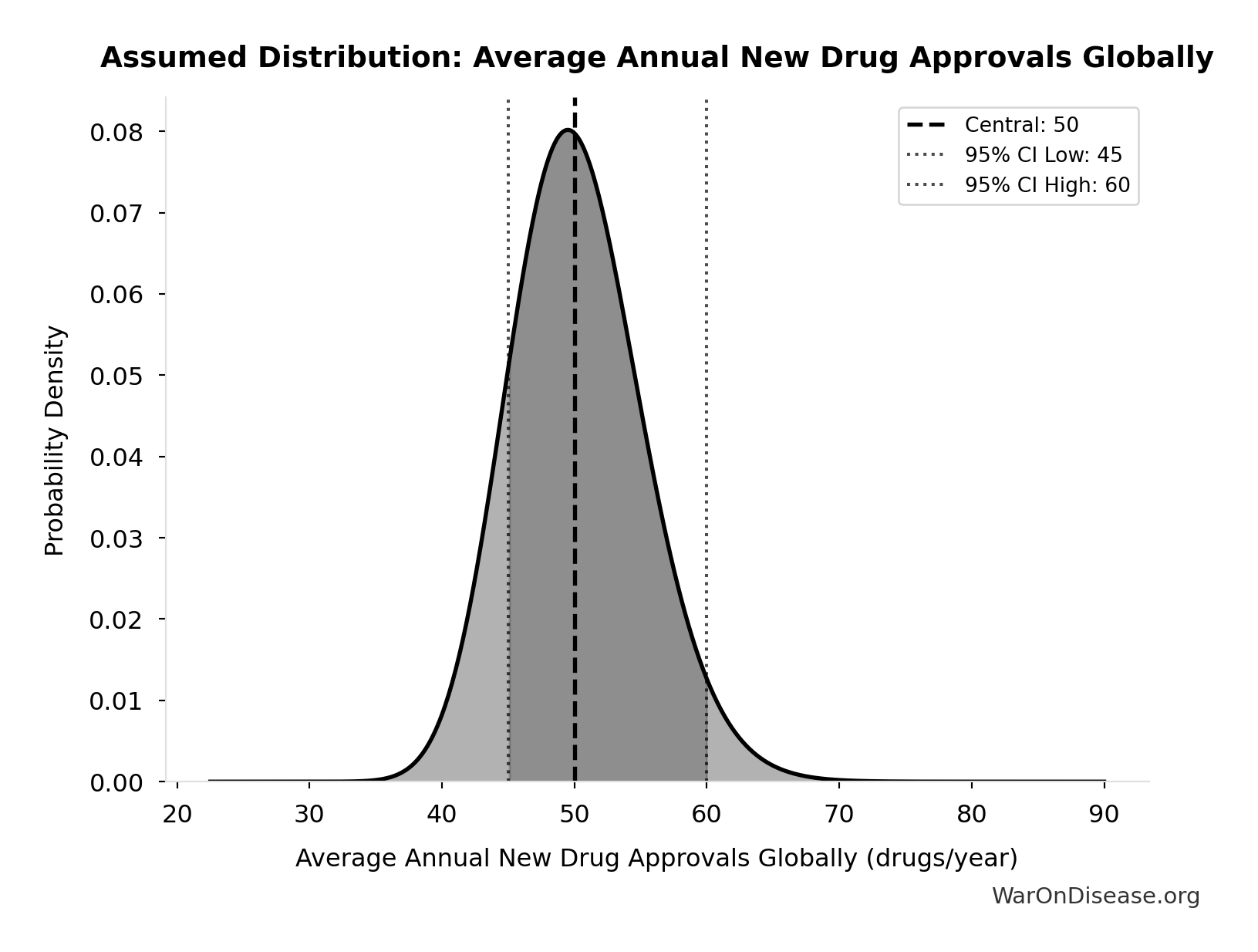
Average Annual New Drug Approvals Globally: 50 drugs/year
Noteπ Details
Average annual new drug approvals globally
Source:29
Uncertainty Range
Technical: 95% CI: [45 drugs/year, 60 drugs/year] β’ Distribution: Lognormal
What this means: This estimate has moderate uncertainty. The true value likely falls between 45 drugs/year and 60 drugs/year (Β±15%). This represents a reasonable range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
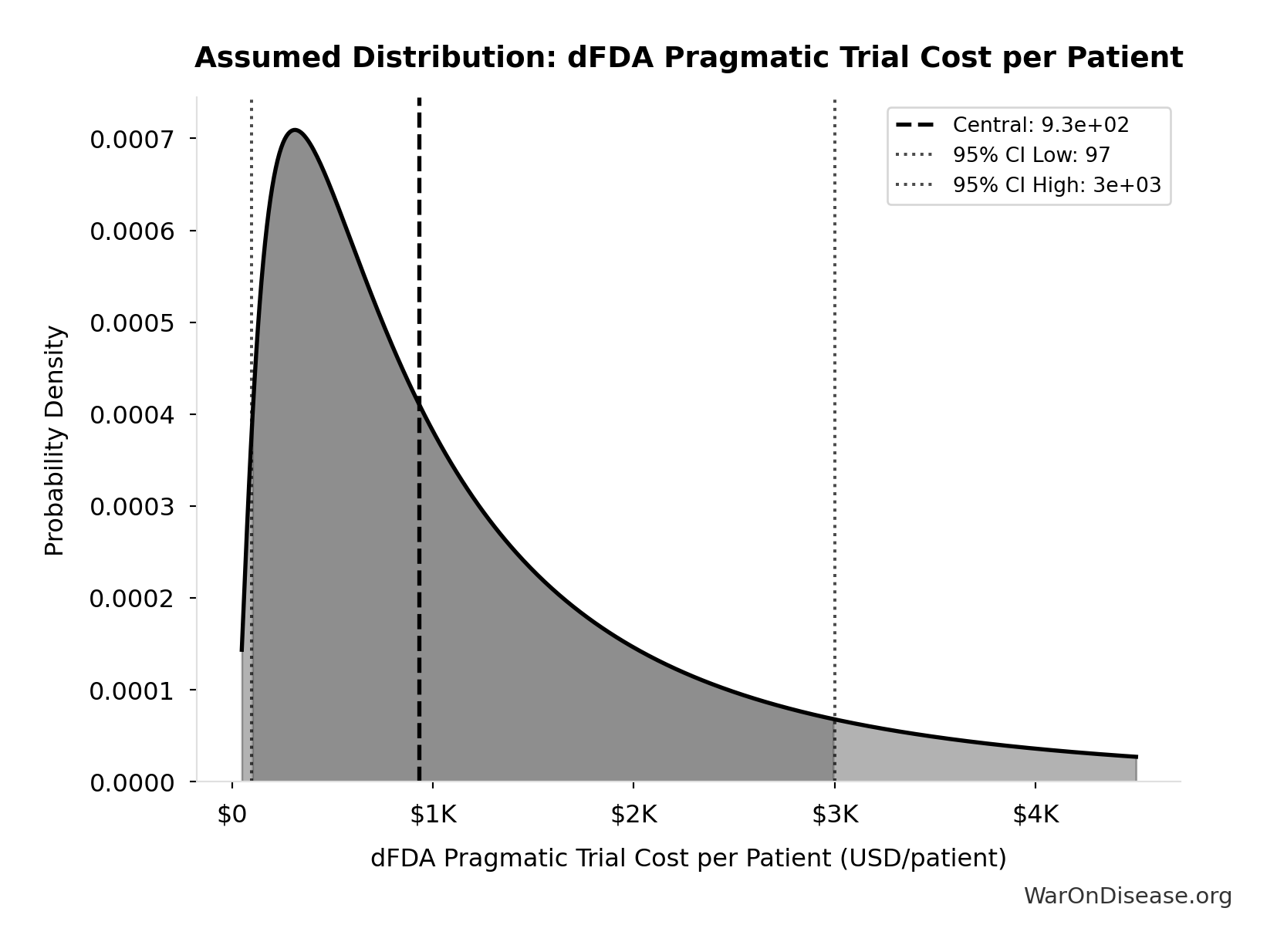
dFDA Pragmatic Trial Cost per Patient: $929
Noteπ Details
dFDA pragmatic trial cost per patient. Uses ADAPTABLE trial ($929) as DELIBERATELY CONSERVATIVE central estimate. Harvard meta-analysis of 108 trials found median of only $97/patient - our estimate may overstate costs by 10x. Confidence interval spans meta-analysis median to complex chronic disease trials.
Source:1
Uncertainty Range
Technical: 95% CI: [$97, $3K] β’ Distribution: Lognormal
What this means: This estimate is highly uncertain. The true value likely falls between $97 and $3K (Β±156%). This represents a very wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence
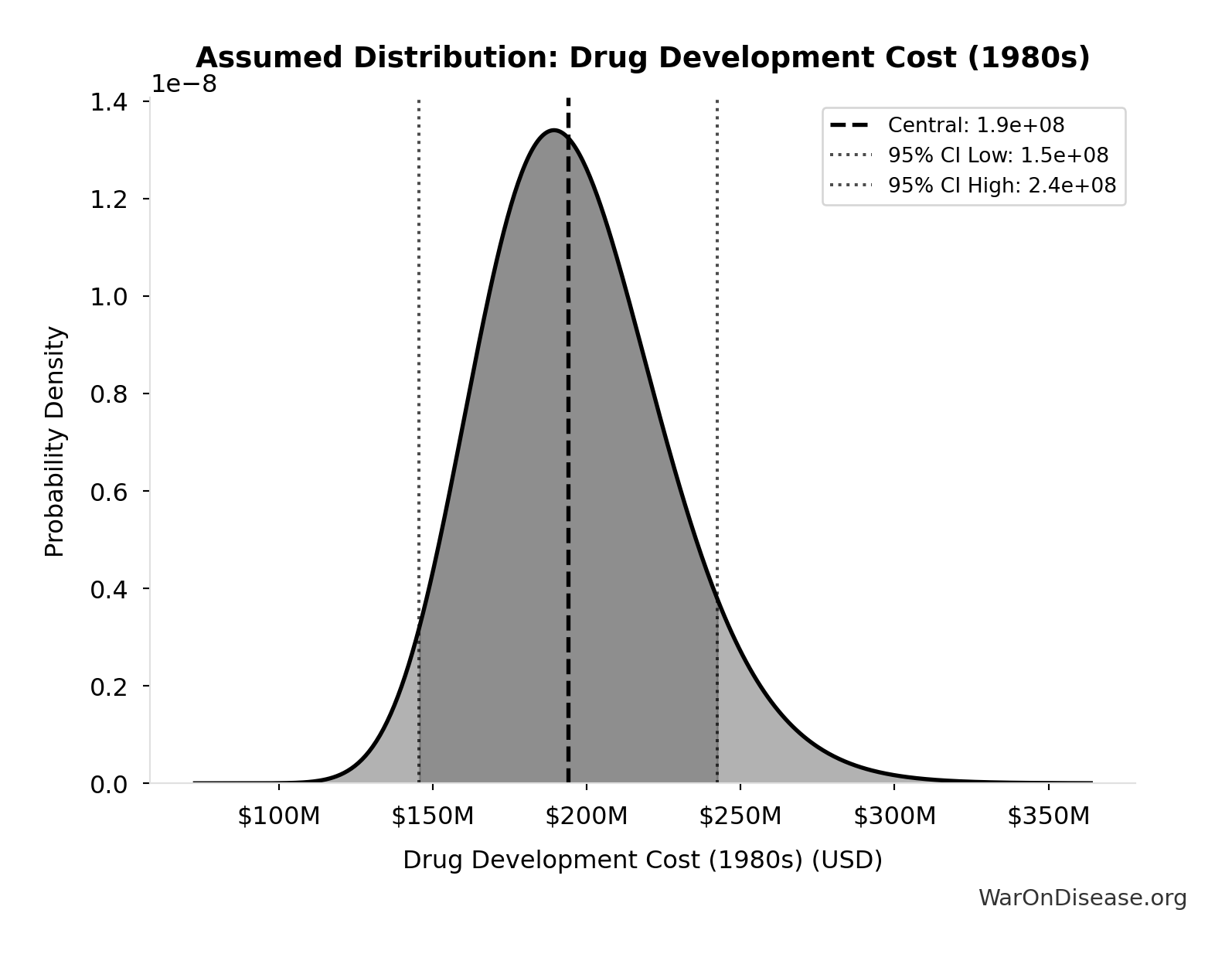
Drug Development Cost (1980s): $194M
Noteπ Details
Drug development cost in 1980s (compounded to approval, 1990 dollars)
Source:35
Uncertainty Range
Technical: 95% CI: [$146M, $242M] β’ Distribution: Lognormal
What this means: This estimate has moderate uncertainty. The true value likely falls between $146M and $242M (Β±25%). This represents a reasonable range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
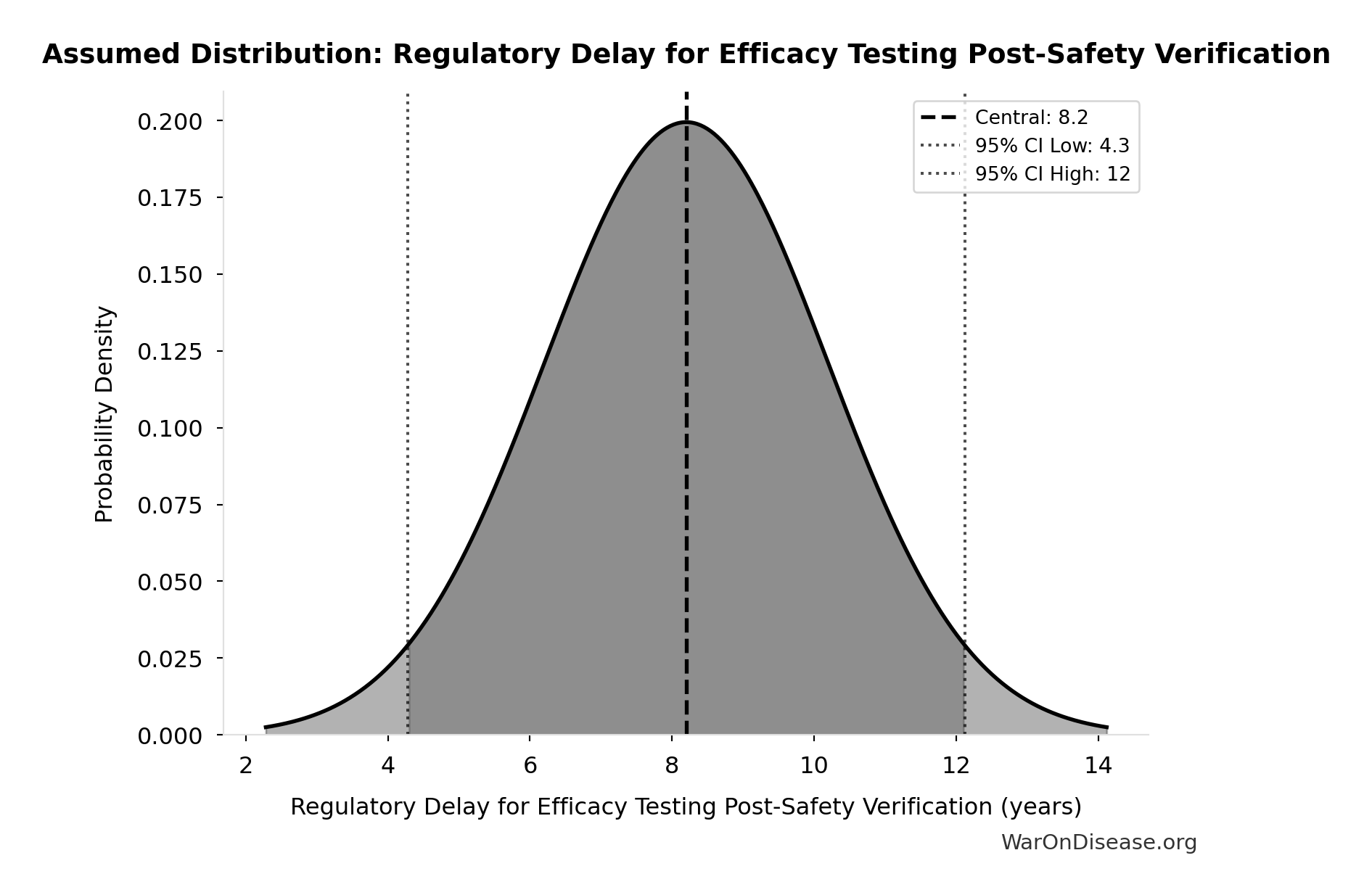
Regulatory Delay for Efficacy Testing Post-Safety Verification: 8.2 years
Noteπ Details
Regulatory delay for efficacy testing (Phase II/III) post-safety verification. Based on BIO 2021 industry survey. Note: This is for drugs that COMPLETE the pipeline - survivor bias means actual delay for any given disease may be longer if candidates fail and must restart.
Source:41
Uncertainty Range
Technical: Distribution: Normal (SE: 2 years)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence β’ π Peer-reviewed β’ Updated 2021
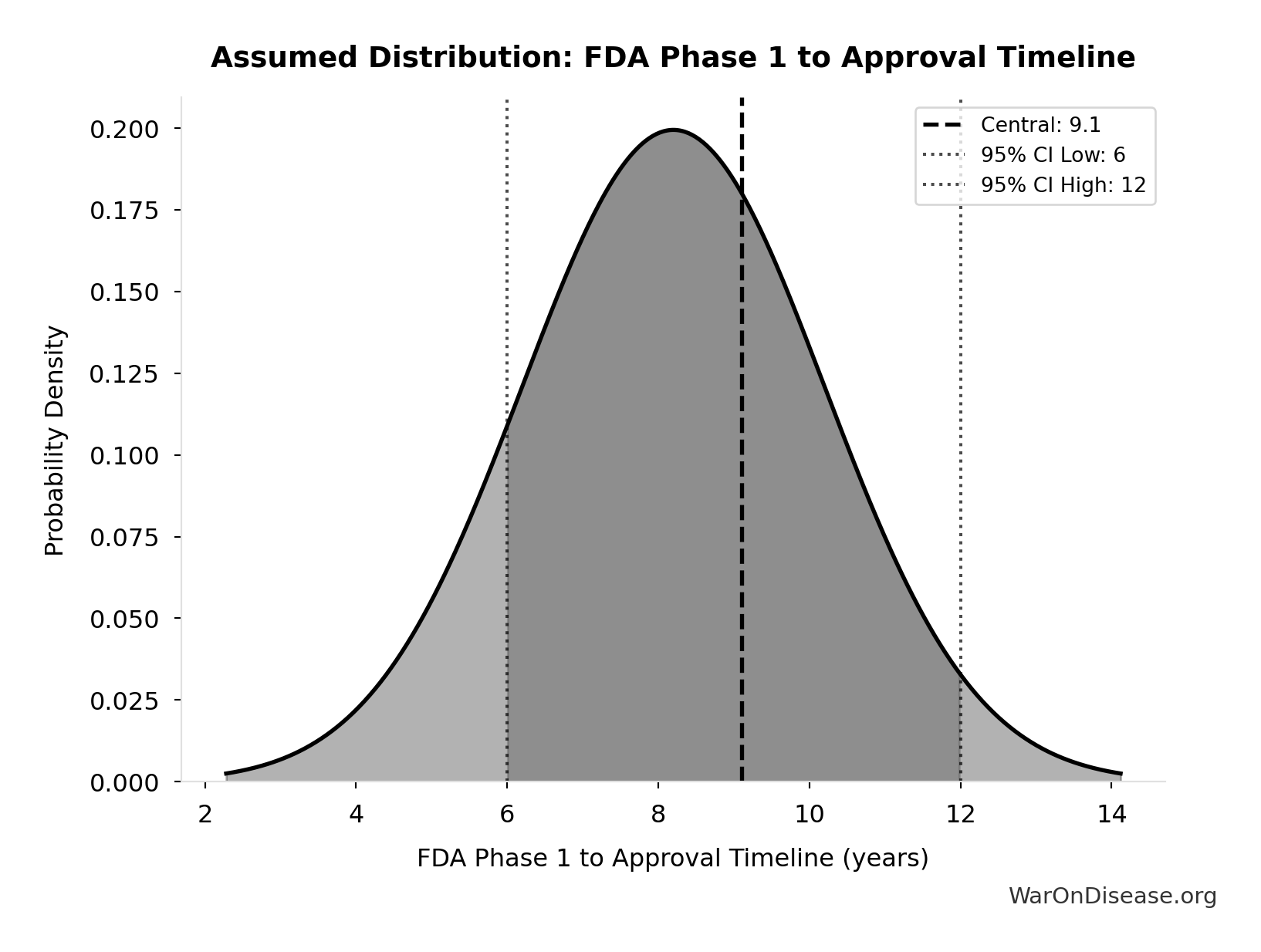
FDA Phase 1 to Approval Timeline: 9.1 years
Noteπ Details
FDA timeline from Phase 1 start to approval (Phase 1-3 + NDA review)
Source:44
Uncertainty Range
Technical: 95% CI: [6 years, 12 years] β’ Distribution: Gamma (SE: 2 years)
What this means: Thereβs significant uncertainty here. The true value likely falls between 6 years and 12 years (Β±33%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The gamma distribution means values follow a specific statistical pattern.
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
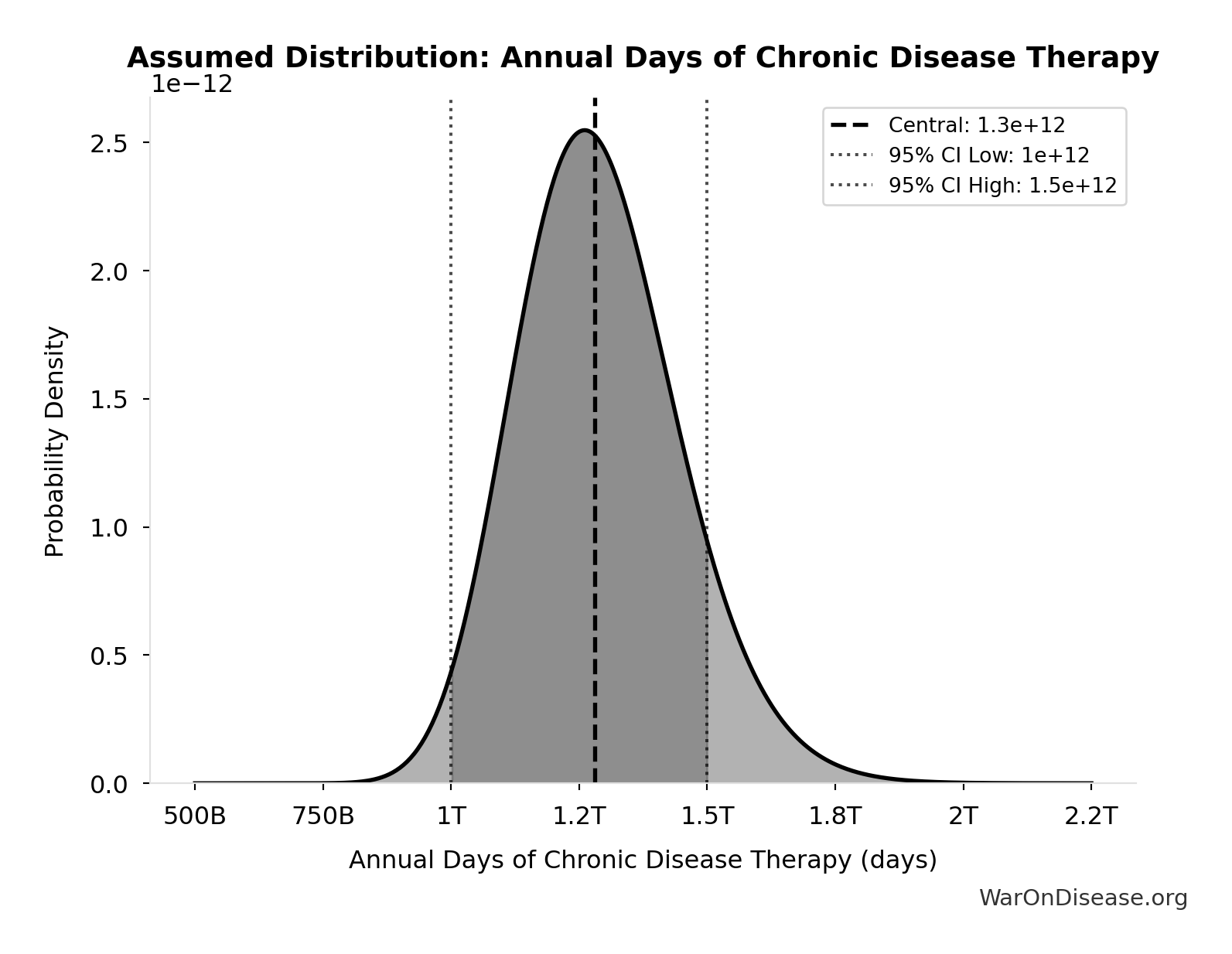
Annual Days of Chronic Disease Therapy: 1.28T days
Noteπ Details
Annual days of therapy for chronic conditions globally (diabetes, CVD, respiratory, cancer). IQVIA reports 1.8 trillion total days of therapy in 2019, with 71% for chronic conditions.
Source:57
Uncertainty Range
Technical: 95% CI: [1.00T days, 1.50T days] β’ Distribution: Lognormal
What this means: This estimate has moderate uncertainty. The true value likely falls between 1.00T days and 1.50T days (Β±20%). This represents a reasonable range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence
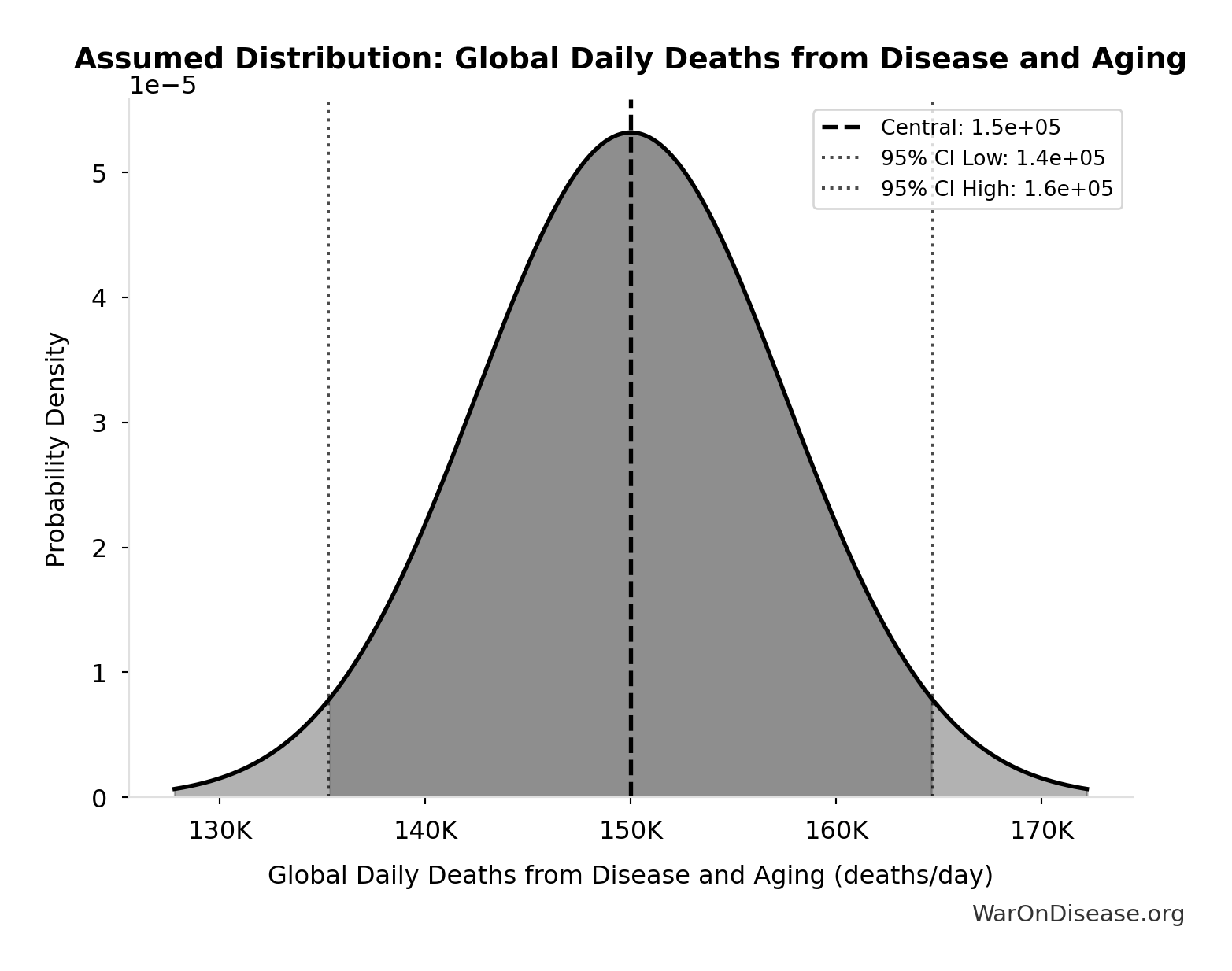
Global Daily Deaths from Disease and Aging: 150k deaths/day
Noteπ Details
Total global deaths per day from all disease and aging (WHO Global Burden of Disease 2024)
Source:18
Uncertainty Range
Technical: Distribution: Normal (SE: 7.50k deaths/day)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence β’ π Peer-reviewed
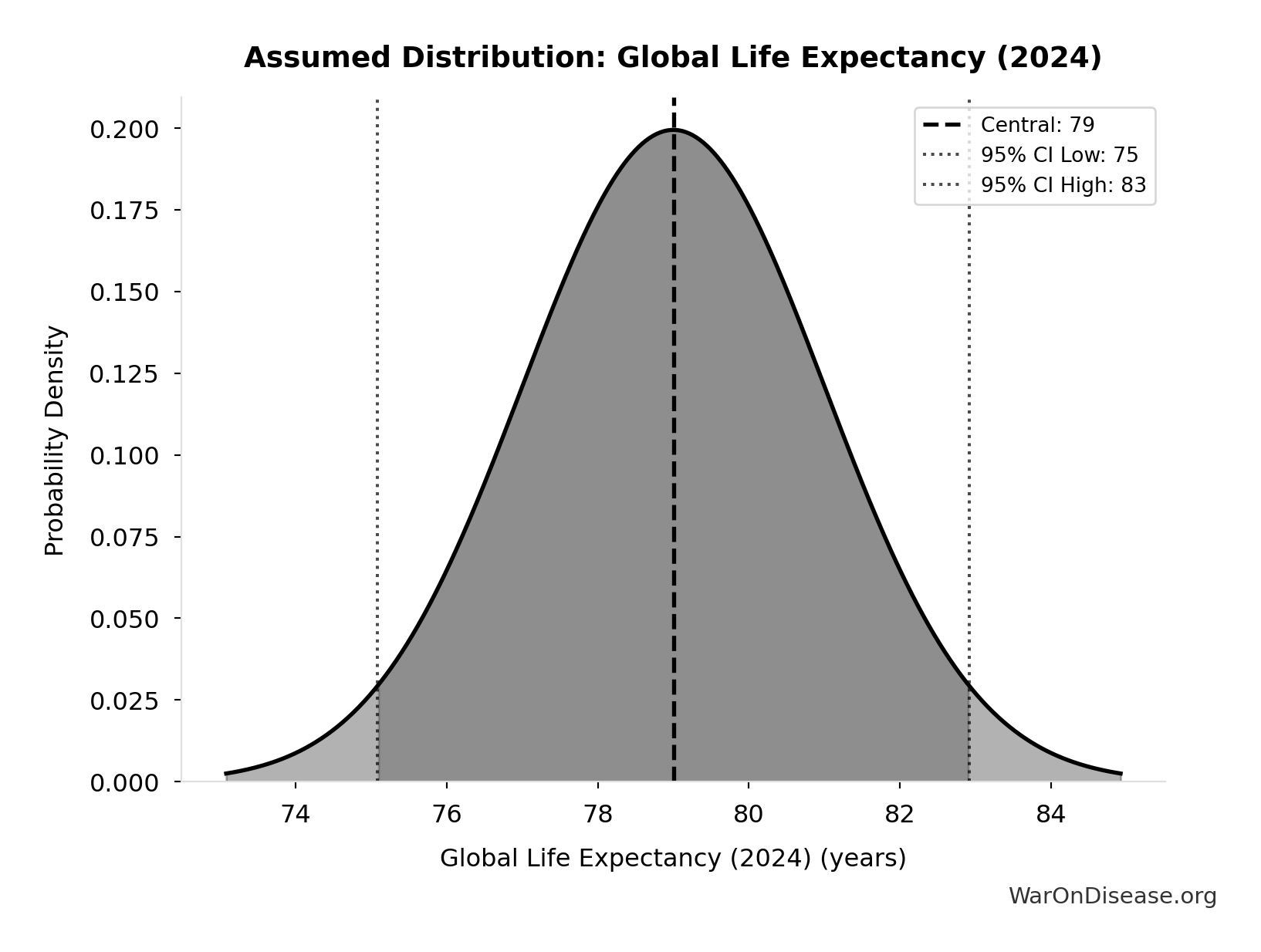
Global Life Expectancy (2024): 79 years
Noteπ Details
Global life expectancy (2024)
Source:18
Uncertainty Range
Technical: Distribution: Normal (SE: 2 years)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence β’ π Peer-reviewed β’ Updated 2024
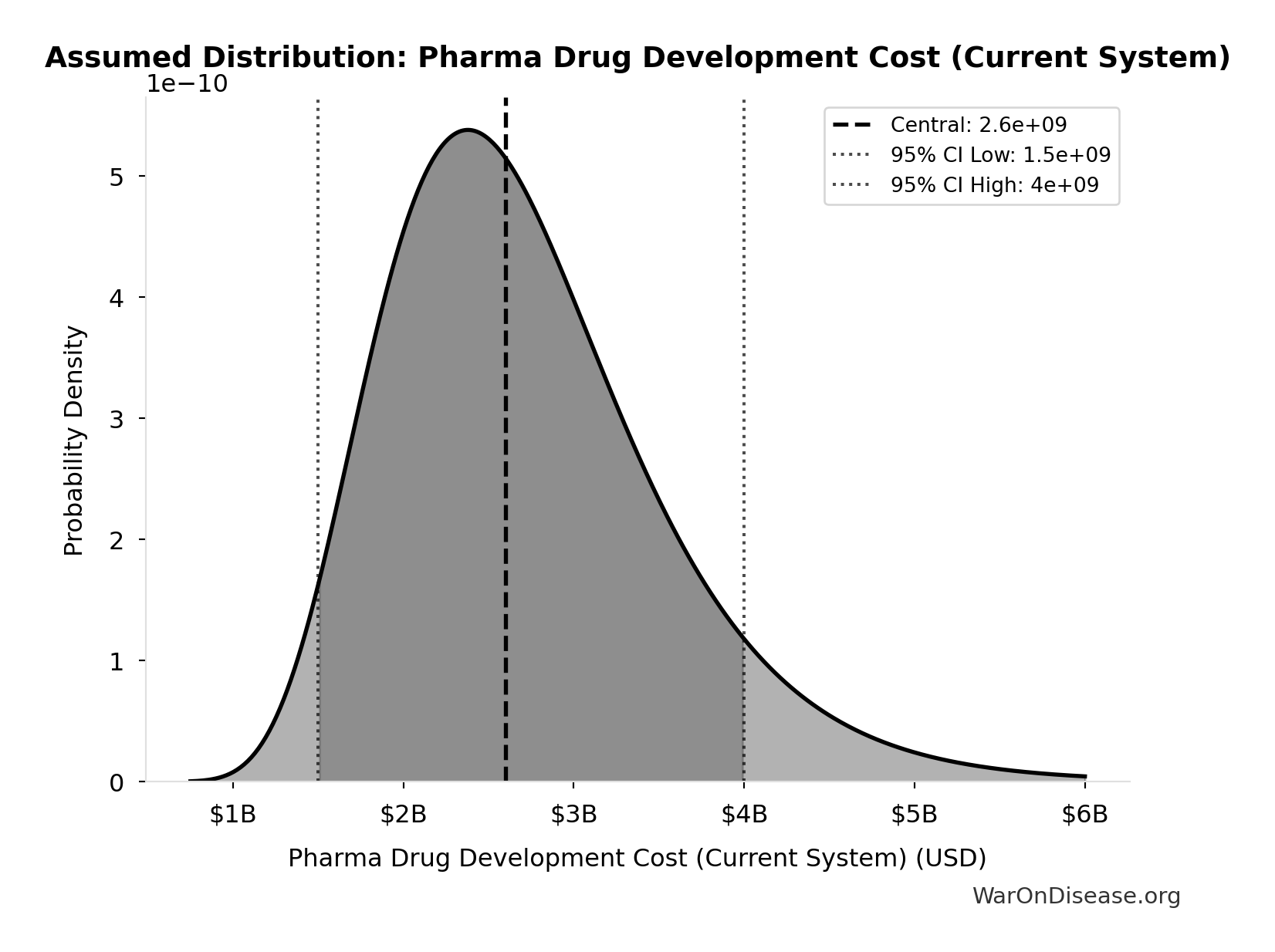
Pharma Drug Development Cost (Current System): $2.60B
Noteπ Details
Average cost to develop one drug in current system
Source:82
Uncertainty Range
Technical: 95% CI: [$1.50B, $4B] β’ Distribution: Lognormal (SE: $500M)
What this means: Thereβs significant uncertainty here. The true value likely falls between $1.50B and $4B (Β±48%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence β’ π Peer-reviewed
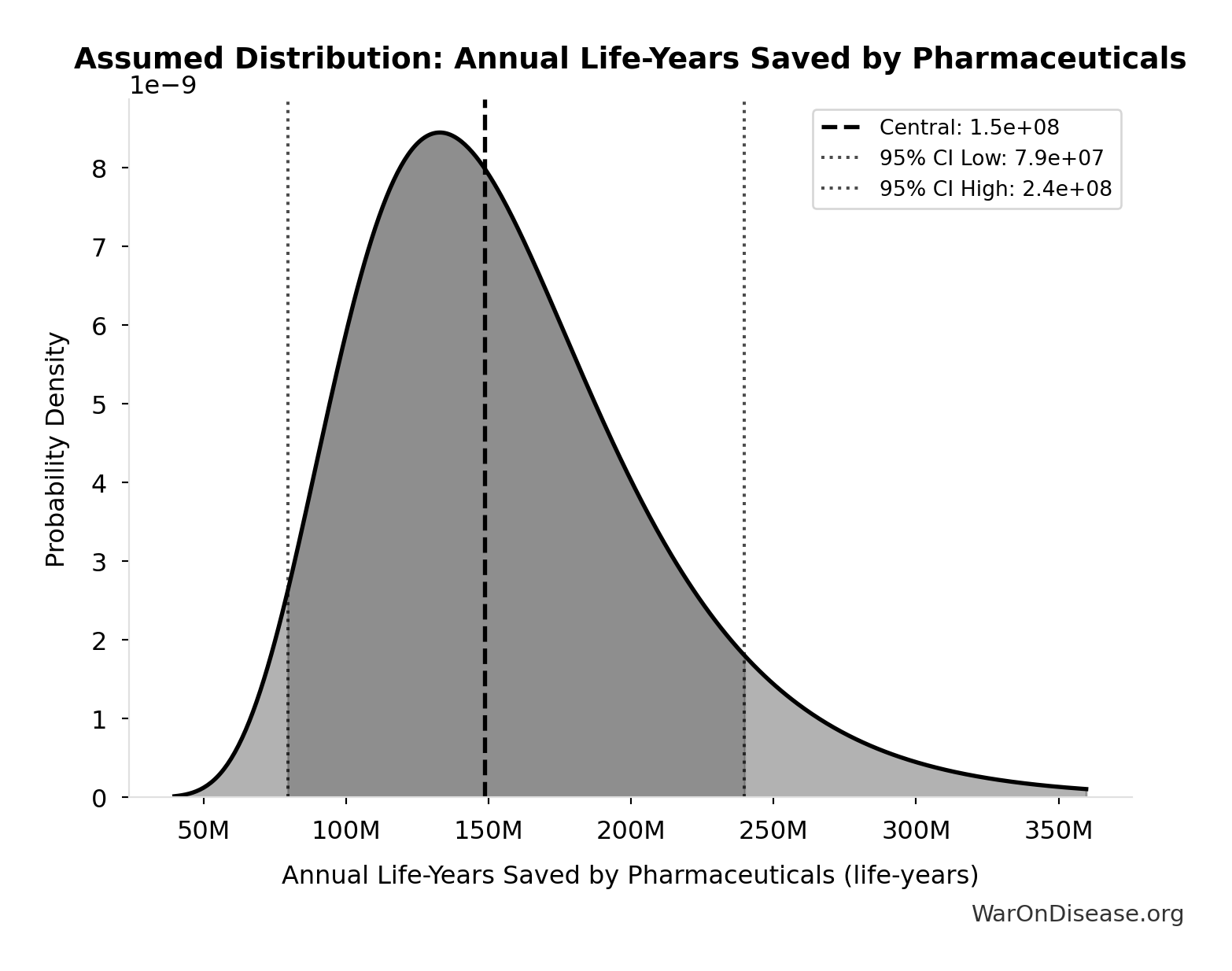
Annual Life-Years Saved by Pharmaceuticals: 149M life-years
Noteπ Details
Annual life-years saved by pharmaceutical innovations globally. Lichtenberg (2019, NBER WP 25483) found that drugs launched after 1981 saved 148.7M life-years in 2013 across 22 countries using 3-way fixed-effects regression (disease-country-year). 95% CI [79.4M, 239.8M] propagated from Table 2 regression standard errors (Ξ²ββββ=-0.031Β±0.008, Ξ²βββ=-0.057Β±0.013).
Source:84
Uncertainty Range
Technical: 95% CI: [79.4M life-years, 240M life-years] β’ Distribution: Lognormal
What this means: This estimate is highly uncertain. The true value likely falls between 79.4M life-years and 240M life-years (Β±54%). This represents a very wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence
Pharma Drug Success Rate (Current System): 10%
Noteπ Details
Percentage of drugs that reach market in current system
Source:86
β High confidence β’ π Peer-reviewed
Phase I Safety Trial Duration: 2.3 years
Noteπ Details
Post-1962 Drug Approval Reduction: 70%
Noteπ Details
Reduction in new drug approvals after 1962 Kefauver-Harris Amendment (70% drop from 43β17 drugs/year)
Source:95
β High confidence β’ Updated 1962-1970
Pre-1962 Physician Count (Unverified): 144k physicians
Noteπ Details
Estimated physicians conducting real-world efficacy trials pre-1962 (unverified estimate)
Source:98
? Low confidence
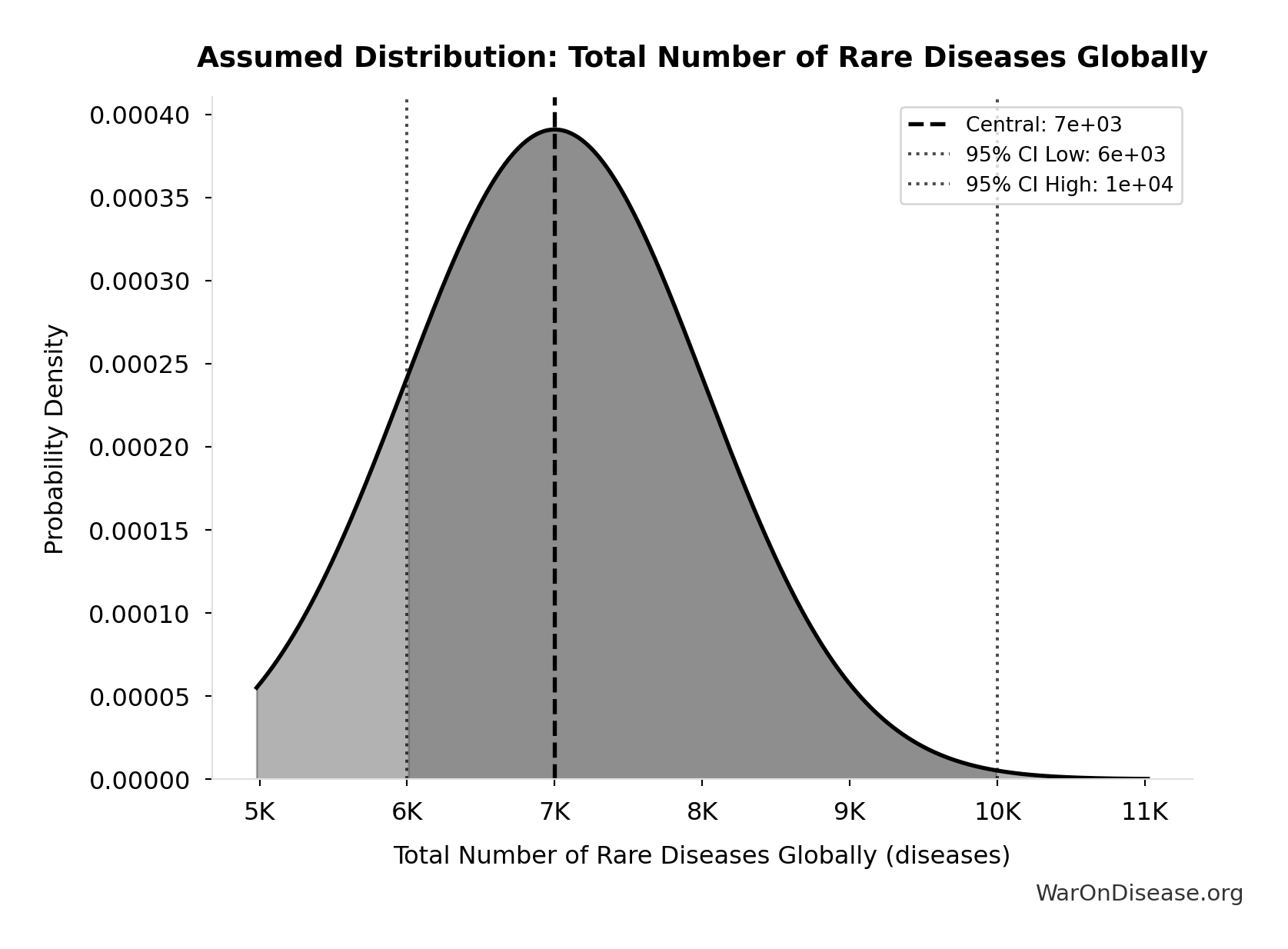
Total Number of Rare Diseases Globally: 7.00k diseases
Noteπ Details
Total number of rare diseases globally
Source:99
Uncertainty Range
Technical: 95% CI: [6.00k diseases, 10.0k diseases] β’ Distribution: Normal
What this means: Thereβs significant uncertainty here. The true value likely falls between 6.00k diseases and 10.0k diseases (Β±29%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The normal distribution means values cluster around the center with equal chances of being higher or lower.
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
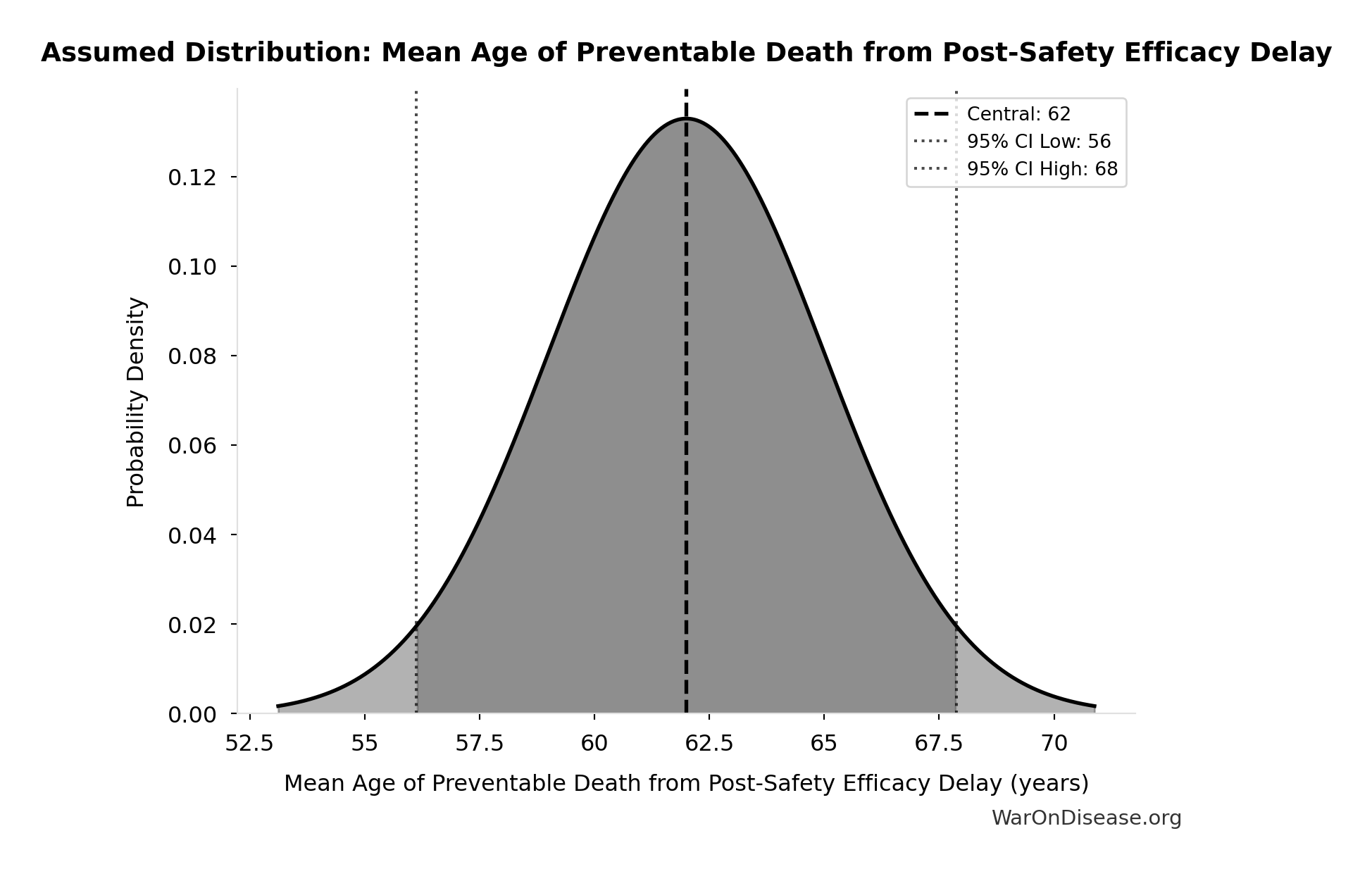
Mean Age of Preventable Death from Post-Safety Efficacy Delay: 62 years
Noteπ Details
Mean age of preventable death from post-safety efficacy testing regulatory delay (Phase 2-4)
Source:18
Uncertainty Range
Technical: Distribution: Normal (SE: 3 years)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence β’ π Peer-reviewed
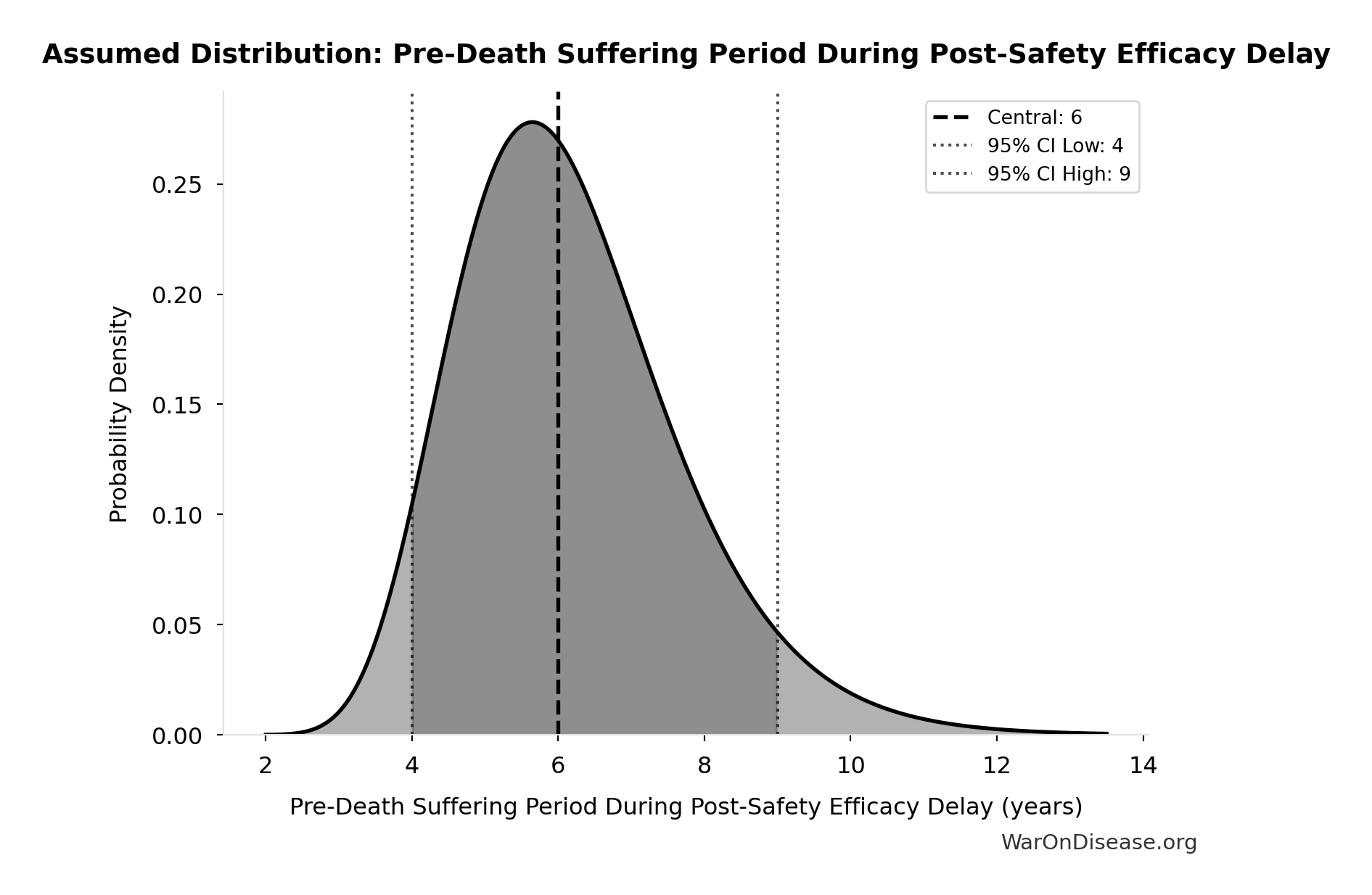
Pre-Death Suffering Period During Post-Safety Efficacy Delay: 6 years
Noteπ Details
Pre-death suffering period during post-safety efficacy testing delay (average years lived with untreated condition while awaiting Phase 2-4 completion)
Source:18
Uncertainty Range
Technical: 95% CI: [4 years, 9 years] β’ Distribution: Lognormal
What this means: Thereβs significant uncertainty here. The true value likely falls between 4 years and 9 years (Β±42%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence β’ π Peer-reviewed
September 11 Deaths: 2.98k people
Noteπ Details
Total deaths in the September 11, 2001 attacks. 2,977 victims (excluding 19 hijackers). Used as a reference point for scale comparisons.
Source:102
Uncertainty Range
Technical: Distribution: Fixed
β High confidence
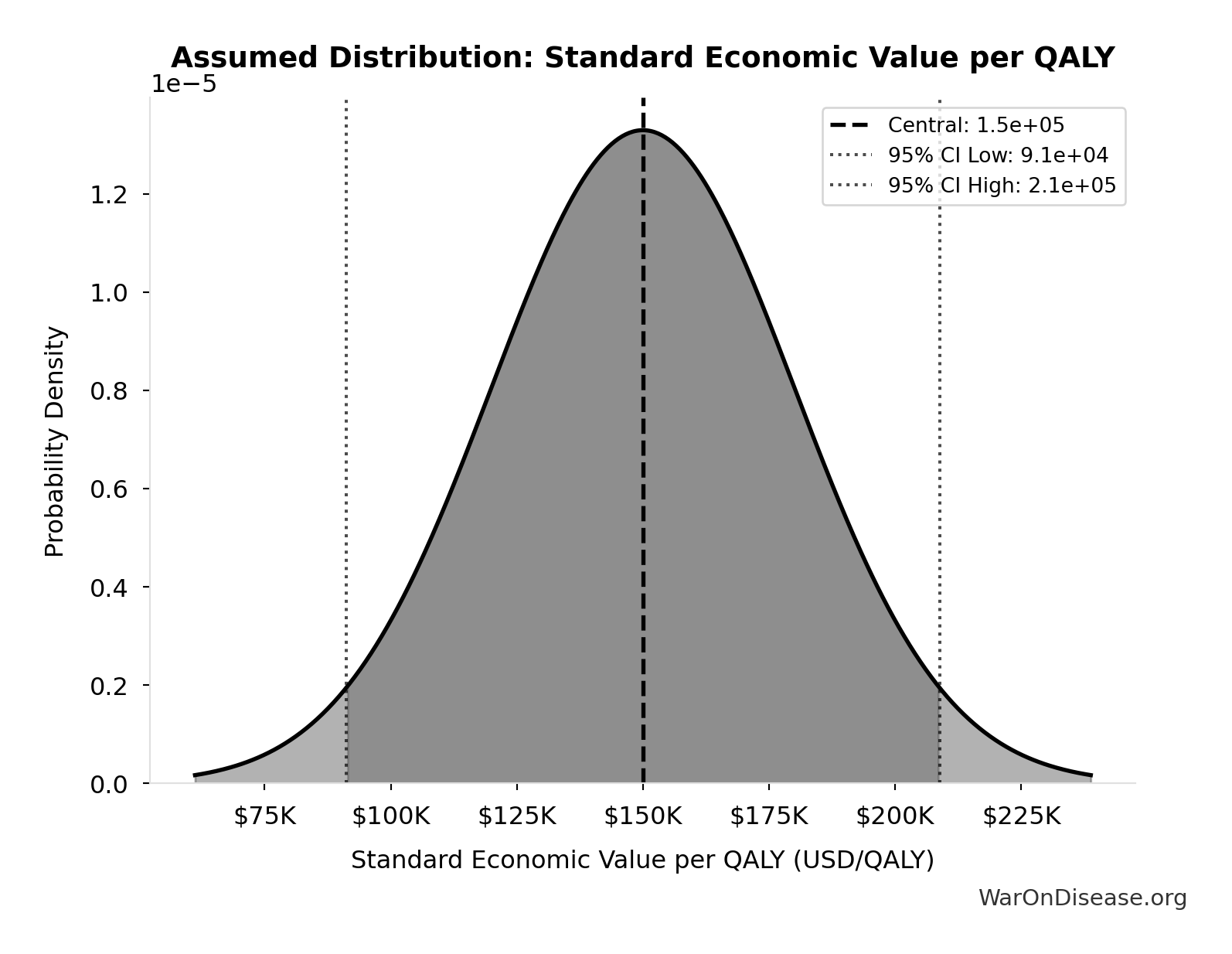
Standard Economic Value per QALY: $150K
Noteπ Details
Standard economic value per QALY
Source:108
Uncertainty Range
Technical: Distribution: Normal (SE: $30K)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
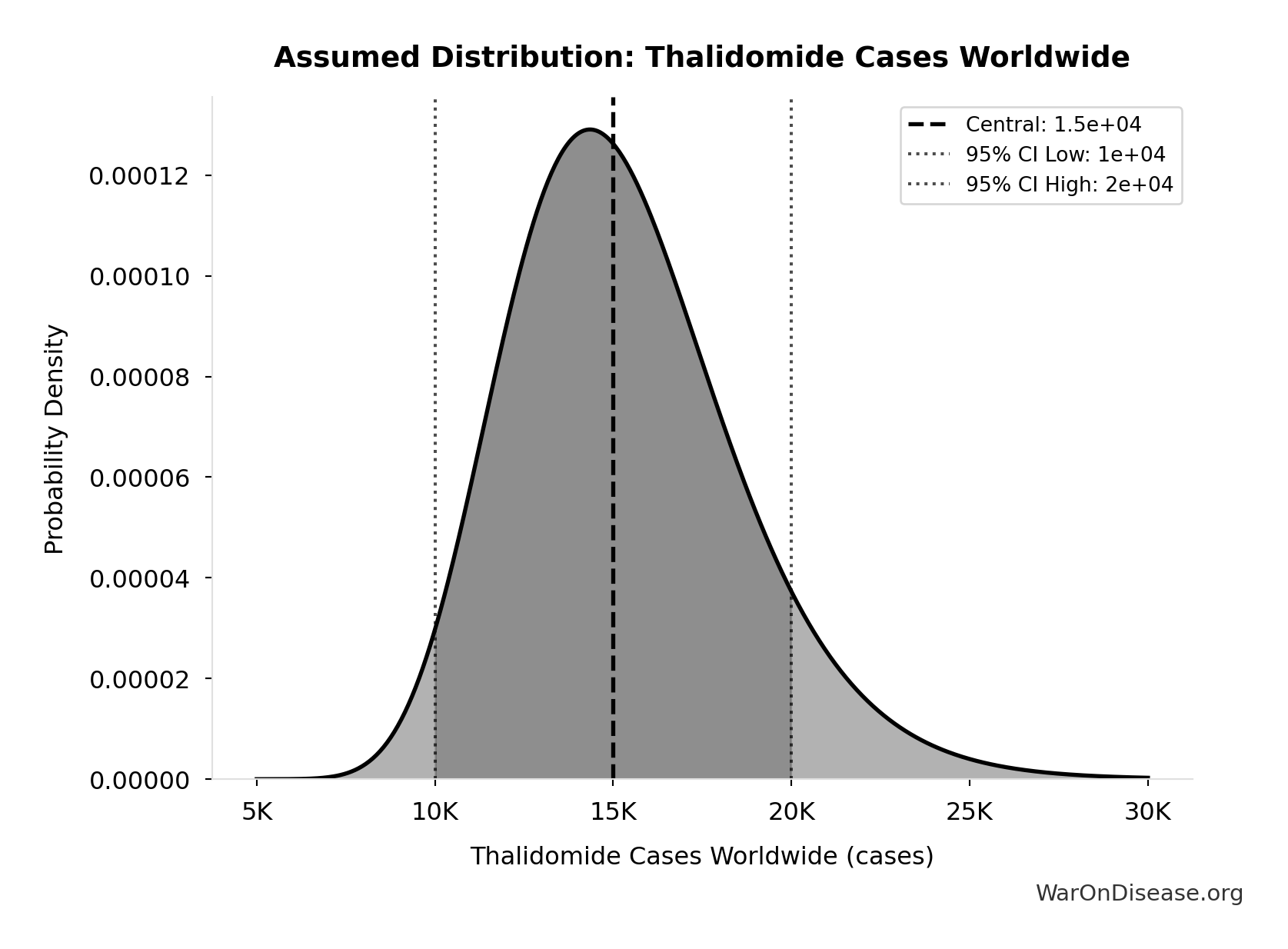
Thalidomide Cases Worldwide: 15.0k cases
Noteπ Details
Total thalidomide birth defect cases worldwide (1957-1962)
Source:115
Uncertainty Range
Technical: 95% CI: [10.0k cases, 20.0k cases] β’ Distribution: Lognormal
What this means: Thereβs significant uncertainty here. The true value likely falls between 10.0k cases and 20.0k cases (Β±33%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence
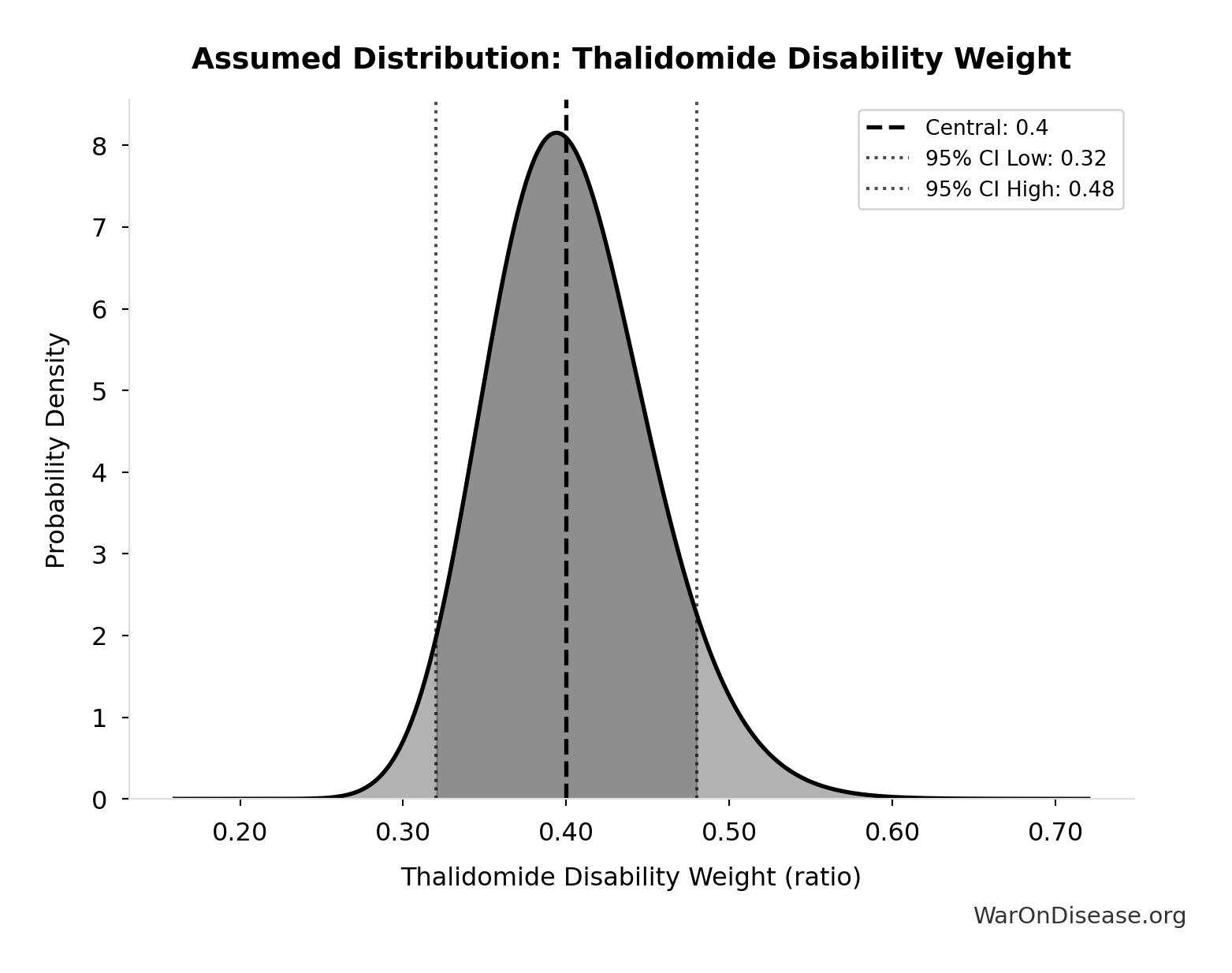
Thalidomide Disability Weight: 0.4:1
Noteπ Details
Disability weight for thalidomide survivors (limb deformities, organ damage)
Source:116
Uncertainty Range
Technical: 95% CI: [0.32:1, 0.48:1] β’ Distribution: Lognormal
What this means: This estimate has moderate uncertainty. The true value likely falls between 0.32:1 and 0.48:1 (Β±20%). This represents a reasonable range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence
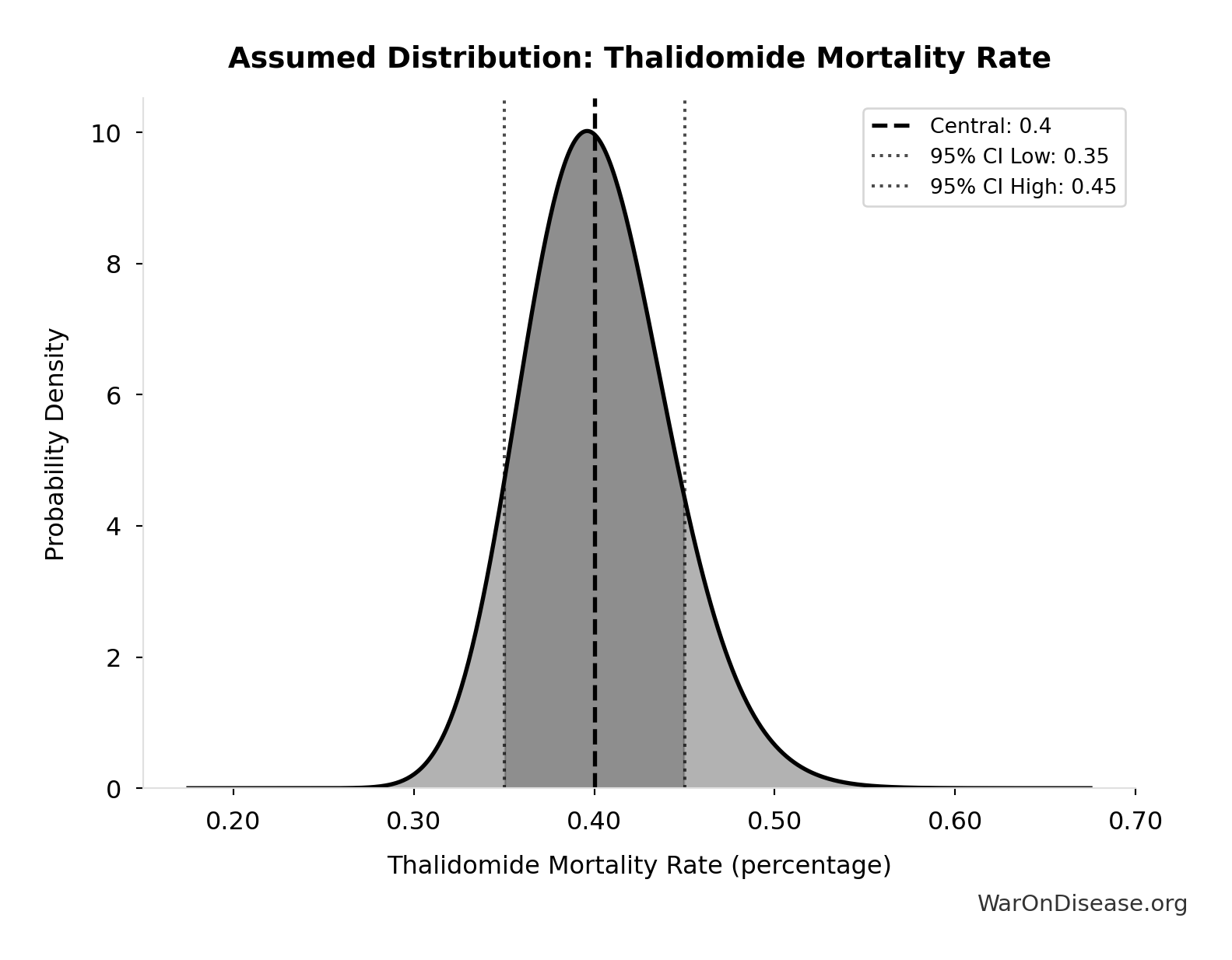
Thalidomide Mortality Rate: 40%
Noteπ Details
Mortality rate for thalidomide-affected infants (died within first year)
Source:115
Uncertainty Range
Technical: 95% CI: [35%, 45%] β’ Distribution: Lognormal
What this means: This estimate has moderate uncertainty. The true value likely falls between 35% and 45% (Β±13%). This represents a reasonable range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
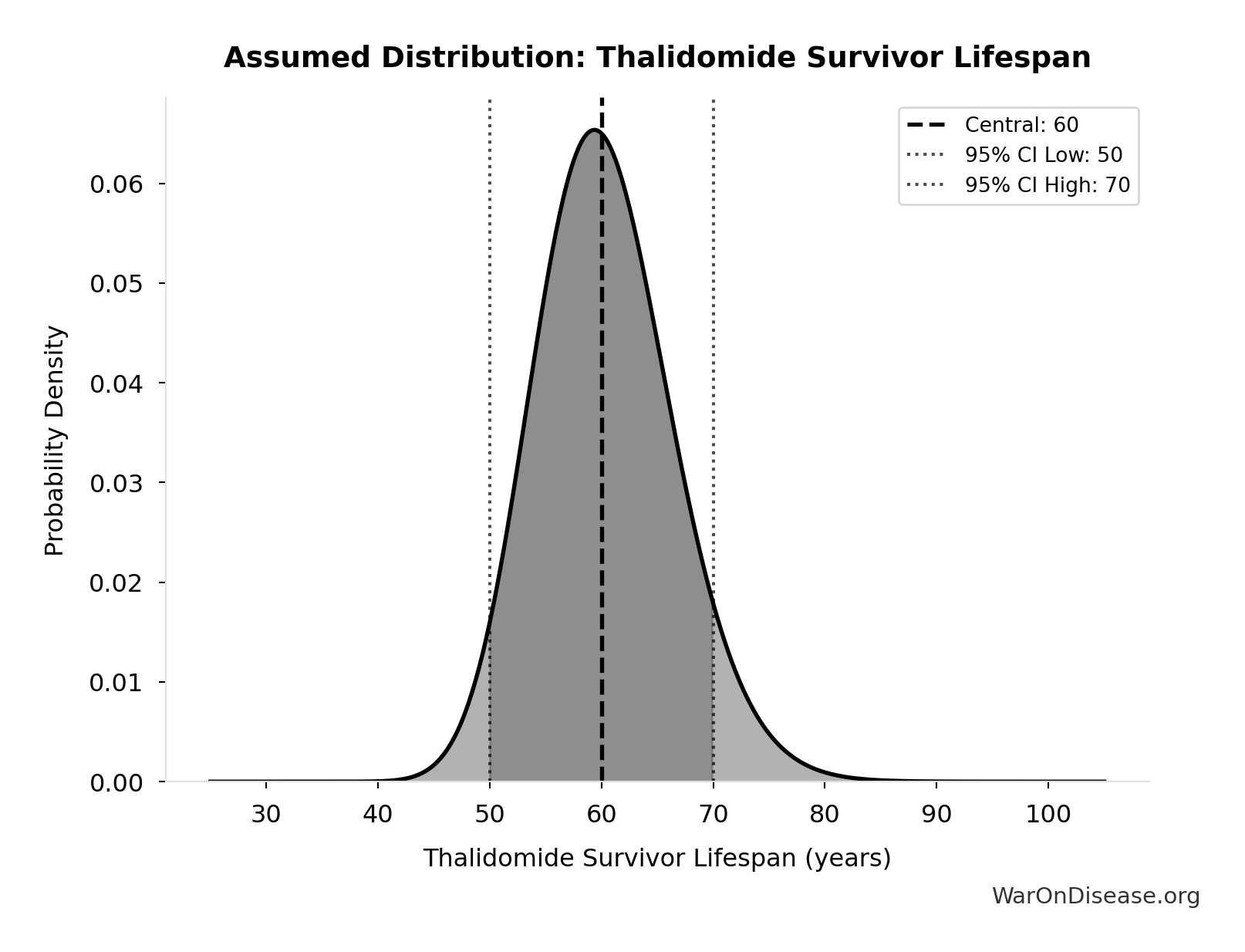
Thalidomide Survivor Lifespan: 60 years
Noteπ Details
Average lifespan for thalidomide survivors
Source:116
Uncertainty Range
Technical: 95% CI: [50 years, 70 years] β’ Distribution: Lognormal
What this means: This estimate has moderate uncertainty. The true value likely falls between 50 years and 70 years (Β±17%). This represents a reasonable range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence
US Population Share 1960: 6%
Noteπ Details
US share of world population in 1960
Source:117
Uncertainty Range
Technical: 95% CI: [5.5%, 6.5%] β’ Distribution: Lognormal
What this means: Weβre quite confident in this estimate. The true value likely falls between 5.5% and 6.5% (Β±8%). This represents a narrow range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
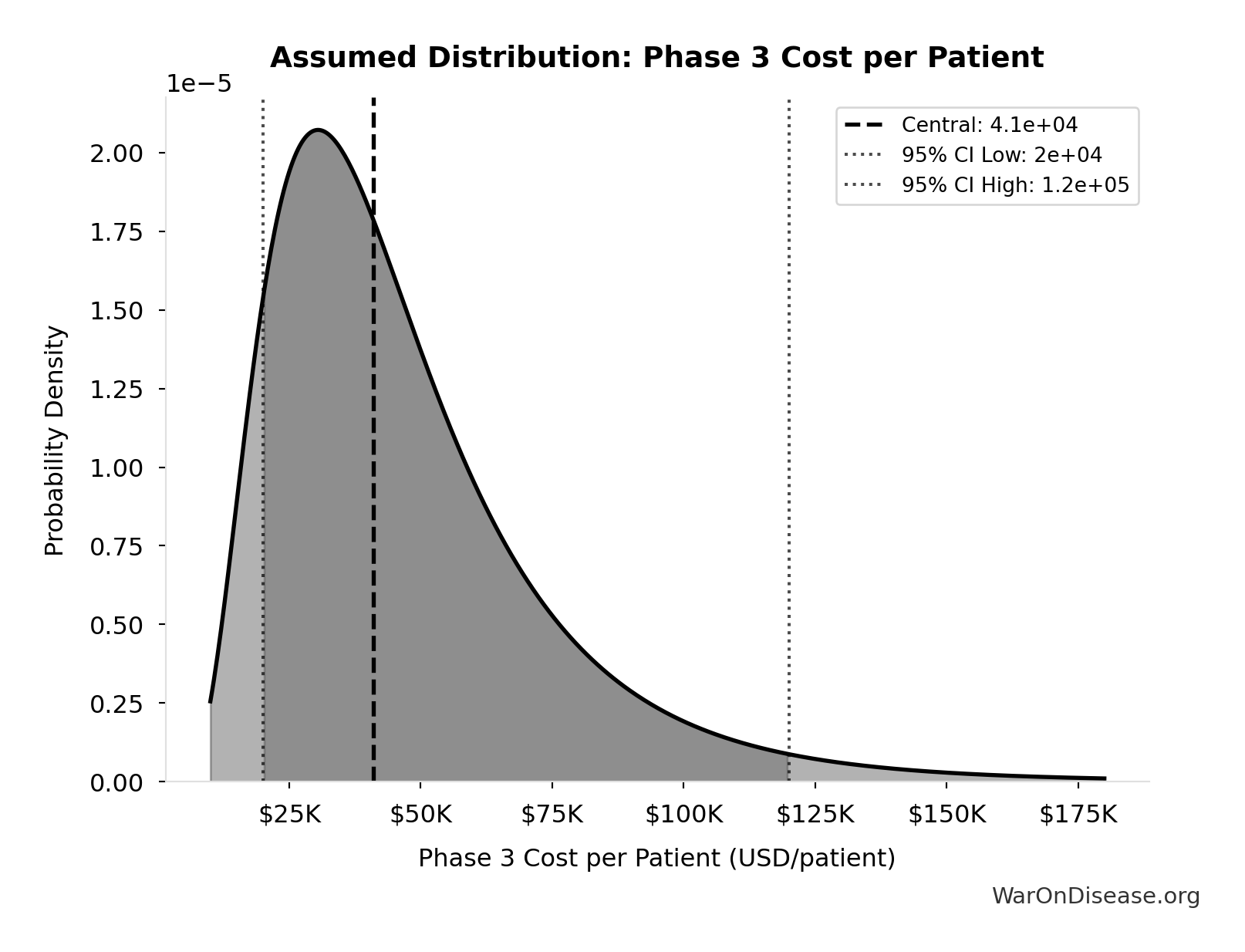
Phase 3 Cost per Patient: $41K
Noteπ Details
Phase 3 cost per patient (median from FDA study)
Source:118
Uncertainty Range
Technical: 95% CI: [$20K, $120K] β’ Distribution: Lognormal
What this means: This estimate is highly uncertain. The true value likely falls between $20K and $120K (Β±122%). This represents a very wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The lognormal distribution means values canβt go negative and have a longer tail toward higher values (common for costs and populations).
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
β High confidence
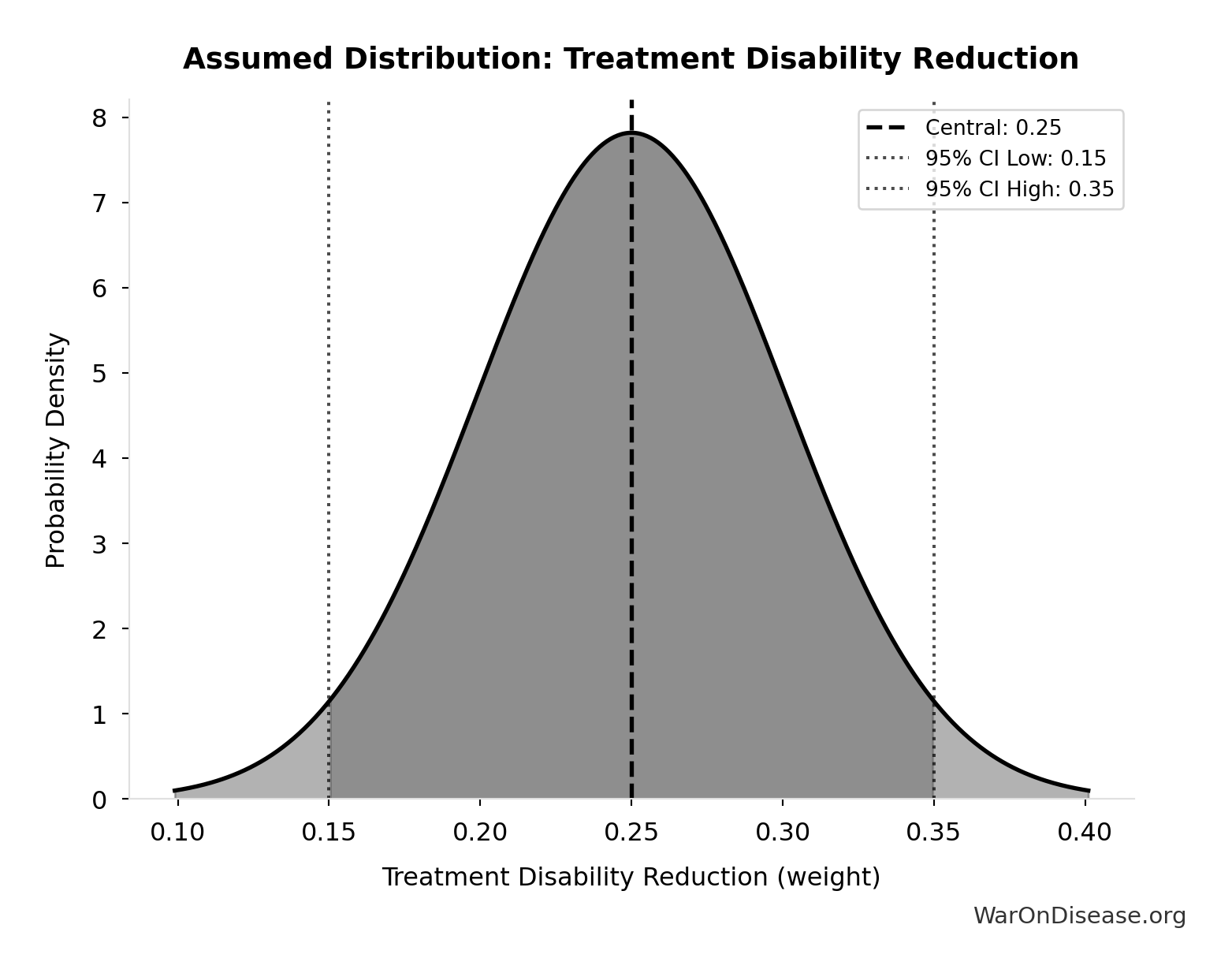
Treatment Disability Reduction: 0.25 weight
Noteπ Details
Average disability weight reduction from pharmaceutical treatment. Untreated chronic disease averages 0.35 disability weight, treated disease averages 0.10, difference is 0.25.
Source:119
Uncertainty Range
Technical: 95% CI: [0.15 weight, 0.35 weight] β’ Distribution: Normal
What this means: Thereβs significant uncertainty here. The true value likely falls between 0.15 weight and 0.35 weight (Β±40%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The normal distribution means values cluster around the center with equal chances of being higher or lower.
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
~ Medium confidence β’ π Peer-reviewed
Core Definitions
Fundamental parameters and constants used throughout the analysis.
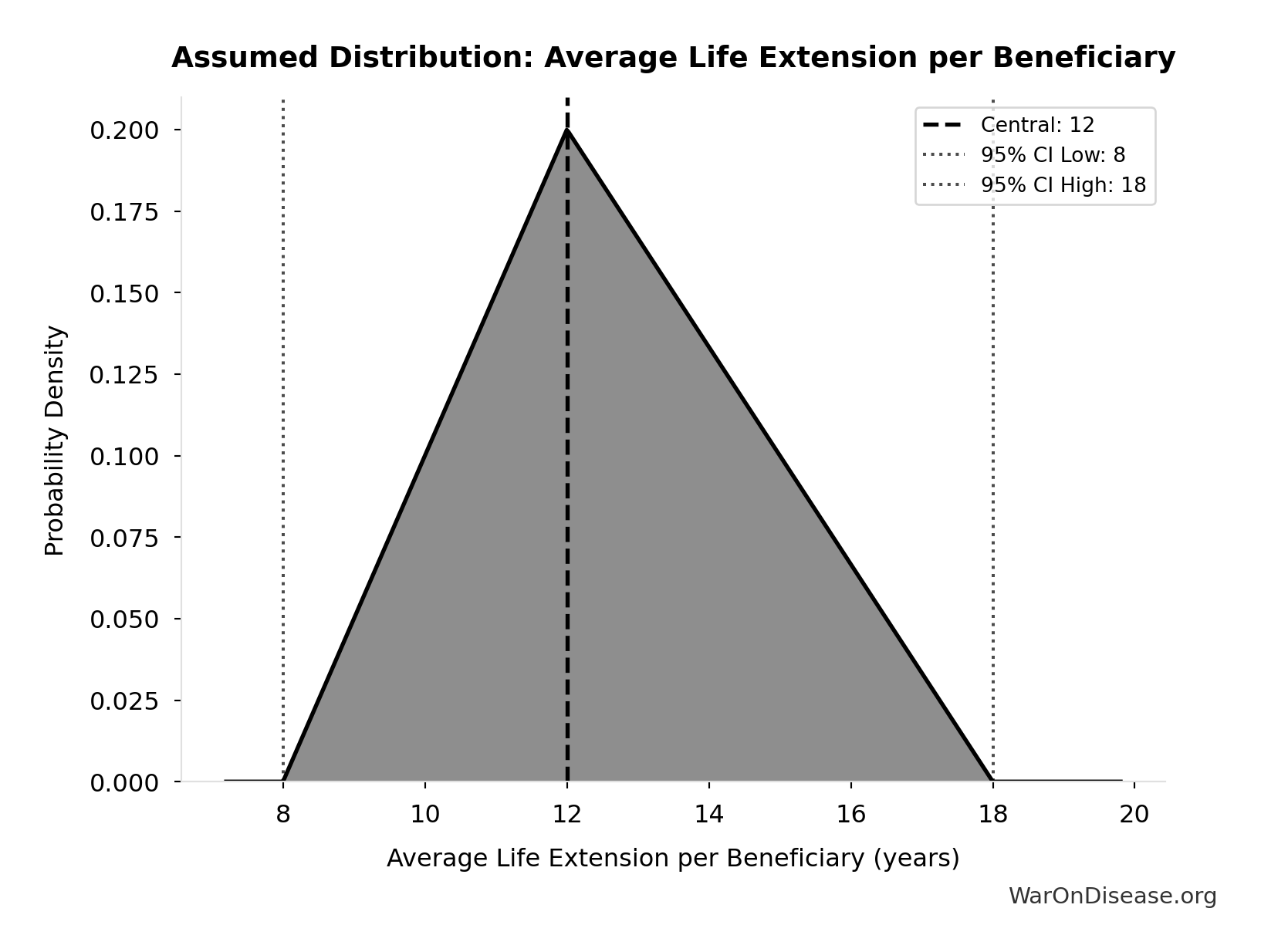
Average Life Extension per Beneficiary: 12 years
Noteπ Details
Average years of life extension per person saved by pharmaceutical interventions. Assumption used to convert life-years saved to approximate lives saved. Based on Lichtenbergβs methodology where life-years are calculated from Years of Life Lost (YLL) reductions.
Uncertainty Range
Technical: 95% CI: [8 years, 18 years] β’ Distribution: Triangular
What this means: Thereβs significant uncertainty here. The true value likely falls between 8 years and 18 years (Β±42%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The triangular distribution means values cluster around a most-likely point but can range higher or lower.
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
Core definition
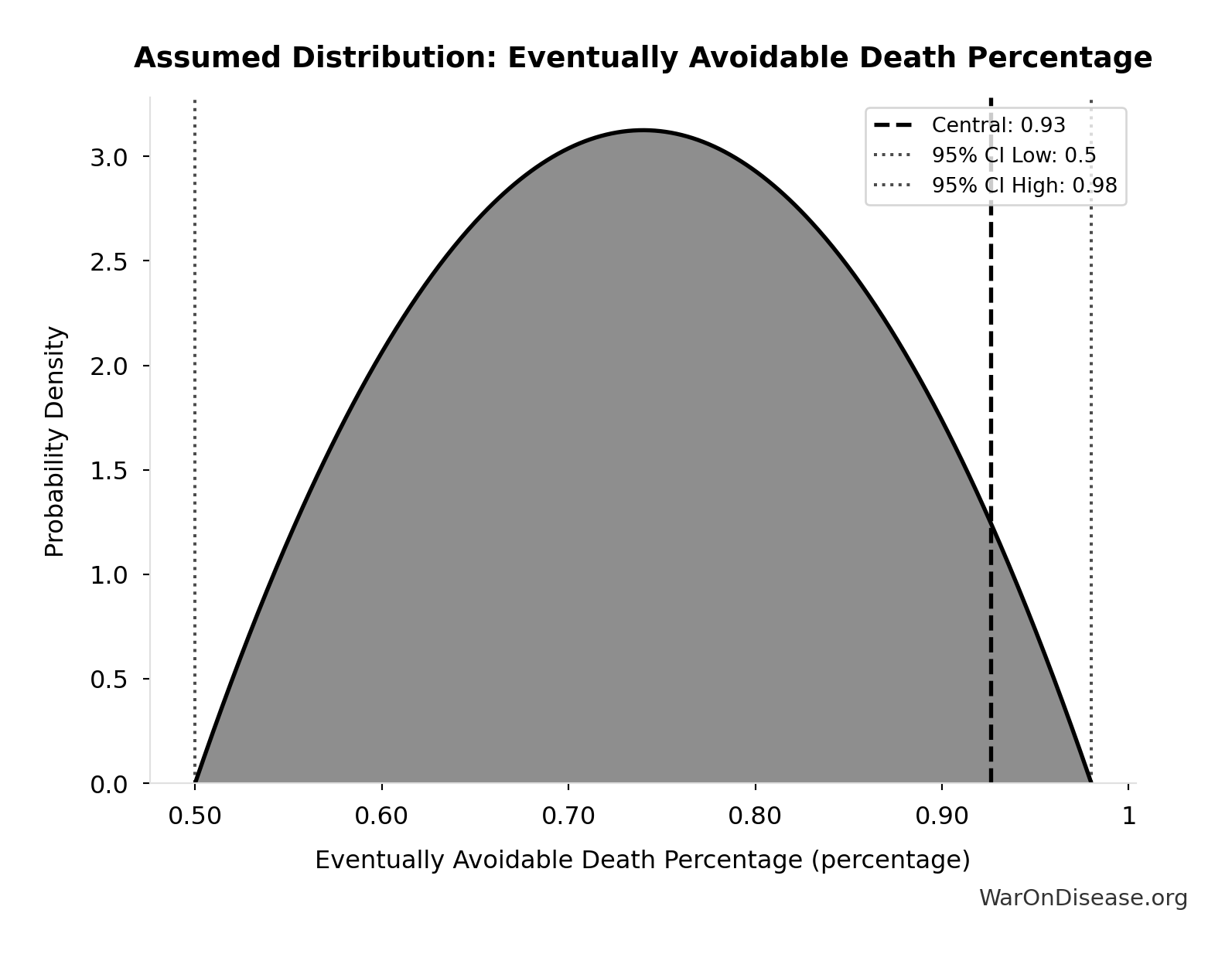
Eventually Avoidable Death Percentage: 92.6%
Noteπ Details
Percentage of deaths that are eventually avoidable with sufficient biomedical research and technological advancement. Central estimate ~92% based on ~7.9% fundamentally unavoidable (primarily accidents). Wide uncertainty reflects debate over: (1) aging as addressable vs. fundamental, (2) asymptotic difficulty of last diseases, (3) multifactorial disease complexity.
Uncertainty Range
Technical: 95% CI: [50%, 98%] β’ Distribution: Beta
What this means: Thereβs significant uncertainty here. The true value likely falls between 50% and 98% (Β±26%). This represents a wide range that our Monte Carlo simulations account for when calculating overall uncertainty in the results.
The beta distribution means values are bounded and can skew toward one end.
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
Core definition
Standard Discount Rate for NPV Analysis: 3%
Noteπ Details
Standard discount rate for NPV analysis (3% annual, social discount rate)
Uncertainty Range
Technical: Distribution: Fixed
Core definition
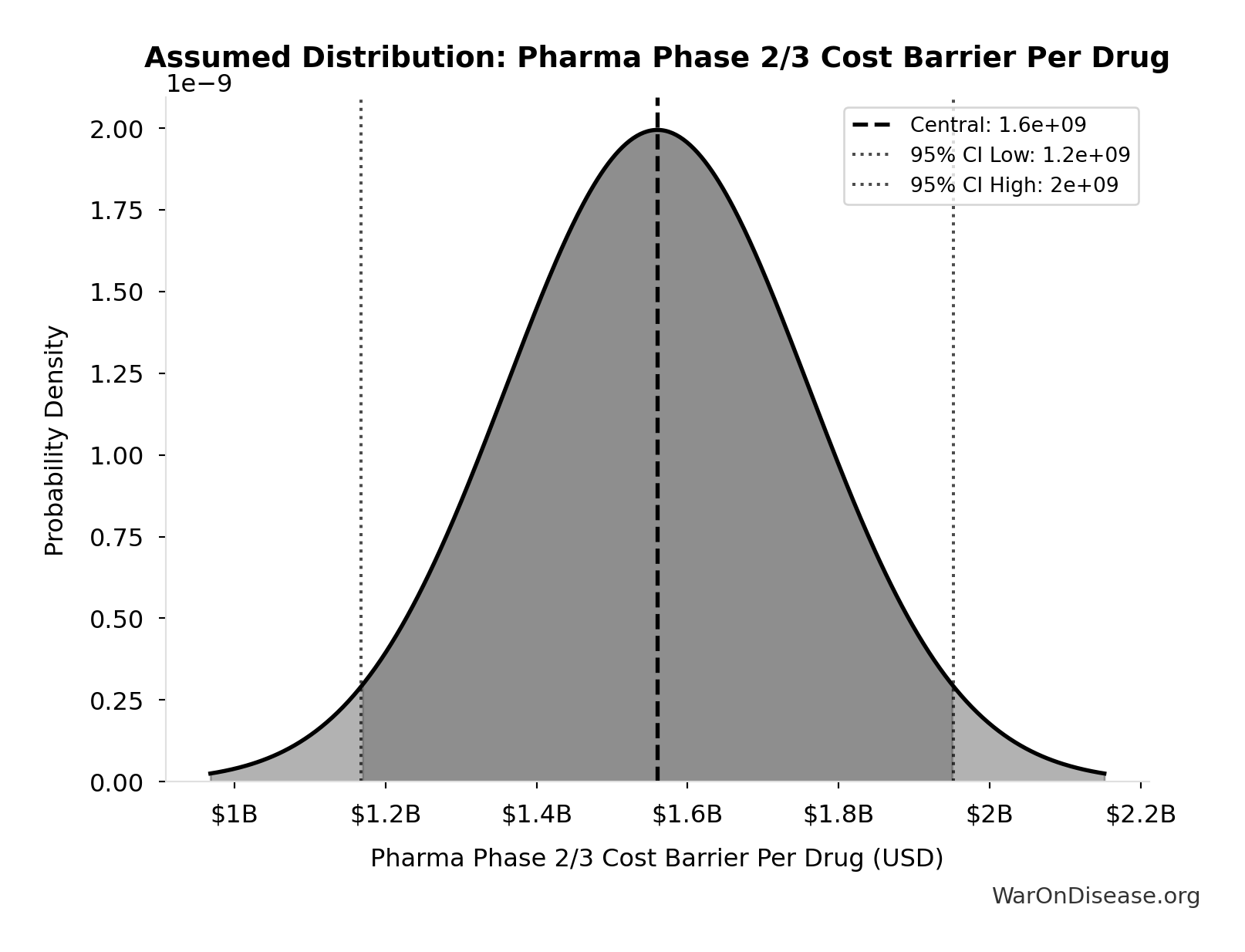
Pharma Phase 2/3 Cost Barrier Per Drug: $1.56B
Noteπ Details
Average Phase 2/3 efficacy testing cost per drug that pharma must fund (~60% of $2.6B total)
Uncertainty Range
Technical: Distribution: Normal (SE: $200M)
Input Distribution
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
Core definition
References
1.
Fund, N. C. NIH pragmatic trials: Minimal funding despite 30x cost advantage. NIH Common Fund: HCS Research Collaboratory https://commonfund.nih.gov/hcscollaboratory (2025)
The NIH Pragmatic Trials Collaboratory funds trials at **$500K for planning phase, $1M/year for implementation**βa tiny fraction of NIHβs budget. The ADAPTABLE trial cost **$14 million** for **15,076 patients** (= **$929/patient**) versus **$420 million** for a similar traditional RCT (30x cheaper), yet pragmatic trials remain severely underfunded. PCORnet infrastructure enables real-world trials embedded in healthcare systems, but receives minimal support compared to basic research funding. Additional sources: https://commonfund.nih.gov/hcscollaboratory | https://pcornet.org/wp-content/uploads/2025/08/ADAPTABLE_Lay_Summary_21JUL2025.pdf | https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5604499/
.2.
NIH. Antidepressant clinical trial exclusion rates. Zimmerman et al. https://pubmed.ncbi.nlm.nih.gov/26276679/ (2015)
Mean exclusion rate: 86.1% across 158 antidepressant efficacy trials (range: 44.4% to 99.8%) More than 82% of real-world depression patients would be ineligible for antidepressant registration trials Exclusion rates increased over time: 91.4% (2010-2014) vs. 83.8% (1995-2009) Most common exclusions: comorbid psychiatric disorders, age restrictions, insufficient depression severity, medical conditions Emergency psychiatry patients: only 3.3% eligible (96.7% excluded) when applying 9 common exclusion criteria Only a minority of depressed patients seen in clinical practice are likely to be eligible for most AETs Note: Generalizability of antidepressant trials has decreased over time, with increasingly stringent exclusion criteria eliminating patients who would actually use the drugs in clinical practice Additional sources: https://pubmed.ncbi.nlm.nih.gov/26276679/ | https://pubmed.ncbi.nlm.nih.gov/26164052/ | https://www.wolterskluwer.com/en/news/antidepressant-trials-exclude-most-real-world-patients-with-depression
.3.
CNBC. Warren buffettβs career average investment return. CNBC https://www.cnbc.com/2025/05/05/warren-buffetts-return-tally-after-60-years-5502284percent.html (2025)
Berkshireβs compounded annual return from 1965 through 2024 was 19.9%, nearly double the 10.4% recorded by the S&P 500. Berkshire shares skyrocketed 5,502,284% compared to the S&P 500βs 39,054% rise during that period. Additional sources: https://www.cnbc.com/2025/05/05/warren-buffetts-return-tally-after-60-years-5502284percent.html | https://www.slickcharts.com/berkshire-hathaway/returns
.4.
BLS. Average US hourly wage. BLS https://www.bls.gov/news.release/pdf/ocwage.pdf (2024)
Mean: $32.66 | Median: $23.80 (May 2024) Additional sources: https://www.bls.gov/news.release/pdf/ocwage.pdf
.5.
Group, E. W. US farm subsidy database and analysis. Environmental Working Group https://farm.ewg.org/ (2024)
US agricultural subsidies total approximately $30 billion annually, but create much larger economic distortions. Top 10% of farms receive 78% of subsidies, benefits concentrated in commodity crops (corn, soy, wheat, cotton), environmental damage from monoculture incentivized, and overall deadweight loss estimated at $50-120 billion annually. Additional sources: https://farm.ewg.org/ | https://www.ers.usda.gov/topics/farm-economy/farm-sector-income-finances/government-payments-the-safety-net/
.6.
Posen, B. R. Restraint: A New Foundation for u.s. Grand Strategy. (Posen, 2014).
The United States could maintain adequate deterrence and defense with a much smaller military budget. Current spending levels reflect force projection capabilities far beyond what homeland security and deterrence require. A strategy of restraint could reduce defense spending by 40-50% while maintaining security through nuclear deterrence and geographic advantages. Additional sources: https://www.cornellpress.cornell.edu/book/9780801452581/restraint/
.7.
Alliance, D. P. The drug war by the numbers. (2021)
Since 1971, the war on drugs has cost the United States an estimated $1 trillion in enforcement. The federal drug control budget was $41 billion in 2022. Mass incarceration costs the U.S. at least $182 billion every year, with over $450 billion spent to incarcerate individuals on drug charges in federal prisons.
8.
Crawford, N. C. & Lutz, C. Blood and treasure: United states budgetary costs and human costs of 20 years of war. (2023)
The total costs of the post-9/11 wars in Iraq, Afghanistan, Pakistan, and Syria are expected to exceed $8 trillion. This includes $2.89 trillion for Iraq/Syria, veterans care through 2050 projected at more than $2 trillion, and interest on war debt adding $6.5 trillion through 2050.
9.
Fund, I. M. IMF fossil fuel subsidies data: 2023 update. (2023)
Globally, fossil fuel subsidies were $7 trillion in 2022 or 7.1 percent of GDP. The United States subsidies totaled $649 billion. Underpricing for local air pollution costs and climate damages are the largest contributor, accounting for about 30 percent each.
10.
Papanicolas, I. et al. Health care spending in the united states and other high-income countries. Papanicolas et al. https://jamanetwork.com/journals/jama/article-abstract/2674671 (2018)
The US spent approximately twice as much as other high-income countries on medical care (mean per capita: $9,892 vs $5,289), with similar utilization but much higher prices. Administrative costs accounted for 8% of US spending vs 1-3% in other countries. US spending on pharmaceuticals was $1,443 per capita vs $749 elsewhere. Despite spending more, US health outcomes are not better. Additional sources: https://jamanetwork.com/journals/jama/article-abstract/2674671
.11.
Hsieh, C.-T. & Moretti, E. Housing constraints and spatial misallocation. Hsieh & Moretti https://www.aeaweb.org/articles?id=10.1257/mac.20170388 (2019)
We quantify the amount of spatial misallocation of labor across US cities and its aggregate costs. Tight land-use restrictions in high-productivity cities like New York, San Francisco, and Boston lowered aggregate US growth by 36% from 1964 to 2009. Local constraints on housing supply have had enormous effects on the national economy. Additional sources: https://www.aeaweb.org/articles?id=10.1257/mac.20170388
.12.
Justice, V. I. of. The economic burden of incarceration in the united states. Vera Institute https://www.vera.org/publications/the-economic-burden-of-incarceration-in-the-u-s (2024)
US incarceration costs approximately $80 billion annually in direct correctional expenditures alone. Including social costs (lost earnings, family impacts, health effects, reduced child outcomes), total burden exceeds $300 billion annually. The US incarcerates at 5x the rate of other OECD countries with no corresponding reduction in crime. Evidence shows community-based alternatives cost less and reduce recidivism more effectively. Additional sources: https://www.vera.org/publications/the-economic-burden-of-incarceration-in-the-u-s | https://www.prisonpolicy.org/reports/pie2024.html | https://www.rand.org/pubs/research_reports/RRA108-3.html
.13.
Marron Institute, N. Transit costs project - why US infrastructure costs so much. NYU Transit Costs Project https://transitcosts.com/ (2024)
The United States builds transit infrastructure at dramatically higher costs than peer countries. New Yorkβs Second Avenue Subway cost $2.5 billion per kilometer vs. $200-500 million in European cities. US highway construction similarly costs 2-5x more than comparable projects abroad. Causes include: excessive environmental review, litigation risk, lack of in-house expertise, fragmented project management, and inflated soft costs. Additional sources: https://transitcosts.com/ | https://www.brookings.edu/articles/why-does-infrastructure-cost-so-much/
.14.
Clemens, M. A. Economics and emigration: Trillion-dollar bills on the sidewalk? Journal of Economic Perspectives 25, 83β106 (2011)
Free global labor mobility would increase gross world product by somewhere in the range of 67-147%... The gains to eliminating migration barriers amount to large fractions of world GDPβone or two orders of magnitude larger than the gains from dropping all remaining restrictions on international flows of goods and capital.
15.
Kleiner, M. M. & Krueger, A. B. Analyzing the extent and influence of occupational licensing on the labor market. Journal of Labor Economics 31, S173βS202 (2013)
Occupational licensing affects 29% of US workers and creates labor market distortions costing 2-3% of GDP.
16.
Lab, Y. B. The fiscal, economic, and distributional effects of all u.s. tariffs. (2025)
Accounting for all the 2025 US tariffs and retaliation implemented to date, the level of real GDP is persistently -0.6% smaller in the long run, the equivalent of $160 billion 2024$ annually.
17.
Foundation, T. Tax compliance costs the US economy $546 billion annually. https://taxfoundation.org/data/all/federal/irs-tax-compliance-costs/ (2024)
Americans will spend over 7.9 billion hours complying with IRS tax filing and reporting requirements in 2024. This costs the economy roughly $413 billion in lost productivity. In addition, the IRS estimates that Americans spend roughly $133 billion annually in out-of-pocket costs, bringing the total compliance costs to $546 billion, or nearly 2 percent of GDP.
18.
Organization, W. H. WHO global health estimates 2024. World Health Organization https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates (2024)
Comprehensive mortality and morbidity data by cause, age, sex, country, and year Global mortality: 55-60 million deaths annually Lives saved by modern medicine (vaccines, cardiovascular drugs, oncology): 12M annually (conservative aggregate) Leading causes of death: Cardiovascular disease (17.9M), Cancer (10.3M), Respiratory disease (4.0M) Note: Baseline data for regulatory mortality analysis. Conservative estimate of pharmaceutical impact based on WHO immunization data (4.5M/year from vaccines) + cardiovascular interventions (3.3M/year) + oncology (1.5M/year) + other therapies. Additional sources: https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates
.19.
GiveWell. GiveWell cost per life saved for top charities (2024). GiveWell: Top Charities https://www.givewell.org/charities/top-charities
General range: $3,000-$5,500 per life saved (GiveWell top charities) Helen Keller International (Vitamin A): $3,500 average (2022-2024); varies $1,000-$8,500 by country Against Malaria Foundation: $5,500 per life saved New Incentives (vaccination incentives): $4,500 per life saved Malaria Consortium (seasonal malaria chemoprevention): $3,500 per life saved VAS program details: $2 to provide vitamin A supplements to child for one year Note: Figures accurate for 2024. Helen Keller VAS program has wide country variation ($1K-$8.5K) but $3,500 is accurate average. Among most cost-effective interventions globally Additional sources: https://www.givewell.org/charities/top-charities | https://www.givewell.org/charities/helen-keller-international | https://ourworldindata.org/cost-effectiveness
.20.
literature, E. psychology. Average reading speed.
Adults: 250 words/minute (silent reading)
.21.
AARP. Unpaid caregiver hours and economic value. AARP 2023 https://www.aarp.org/caregiving/financial-legal/info-2023/unpaid-caregivers-provide-billions-in-care.html (2023)
Average family caregiver: 25-26 hours per week (100-104 hours per month) 38 million caregivers providing 36 billion hours of care annually Economic value: $16.59 per hour = $600 billion total annual value (2021) 28% of people provided eldercare on a given day, averaging 3.9 hours when providing care Caregivers living with care recipient: 37.4 hours per week Caregivers not living with recipient: 23.7 hours per week Note: Disease-related caregiving is subset of total; includes elderly care, disability care, and child care Additional sources: https://www.aarp.org/caregiving/financial-legal/info-2023/unpaid-caregivers-provide-billions-in-care.html | https://www.bls.gov/news.release/elcare.nr0.htm | https://www.caregiver.org/resource/caregiver-statistics-demographics/
.22.
MMWR, C. Childhood vaccination economic benefits. CDC MMWR https://www.cdc.gov/mmwr/volumes/73/wr/mm7331a2.htm (1994)
US programs (1994-2023): $540B direct savings, $2.7T societal savings ( $18B/year direct, $90B/year societal) Global (2001-2020): $820B value for 10 diseases in 73 countries ( $41B/year) ROI: $11 return per $1 invested Measles vaccination alone saved 93.7M lives (61% of 154M total) over 50 years (1974-2024) Additional sources: https://www.cdc.gov/mmwr/volumes/73/wr/mm7331a2.htm | https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(24
.23.
CDC. Childhood vaccination (US) ROI. CDC https://www.cdc.gov/mmwr/preview/mmwrhtml/mm6316a4.htm (2017).
24.
Labor Statistics, U. S. B. of. CPI inflation calculator. (2024)
CPI-U (1980): 82.4 CPI-U (2024): 313.5 Inflation multiplier (1980-2024): 3.80Γ Cumulative inflation: 280.48% Average annual inflation rate: 3.08% Note: Official U.S. government inflation data using Consumer Price Index for All Urban Consumers (CPI-U). Additional sources: https://www.bls.gov/data/inflation_calculator.htm
.25.
Del Rosal, I. The empirical measurement of rent-seeking costs. Journal of Economic Surveys https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-6419.2009.00621.x (2011)
A comprehensive survey of empirical estimates finds rent-seeking costs range from 0.2% to 23.7% of GDP across different methodologies and countries. Laband & Sophocleus (1988) estimated up to 45% for the US.
26.
via, D. analysis. ClinicalTrials.gov cumulative enrollment data (2025). Direct analysis via ClinicalTrials.gov API v2 https://clinicaltrials.gov/data-api/api
Analysis of 100,000 active/recruiting/completed trials on ClinicalTrials.gov (November 2025) shows cumulative enrollment of 12.2 million participants: Phase 1 (722k), Phase 2 (2.2M), Phase 3 (6.5M), Phase 4 (2.7M). Median participants per trial: Phase 1 (33), Phase 2 (60), Phase 3 (237), Phase 4 (90). Additional sources: https://clinicaltrials.gov/data-api/api
.27.
CAN, A. Clinical trial patient participation rate. ACS CAN: Barriers to Clinical Trial Enrollment https://www.fightcancer.org/policy-resources/barriers-patient-enrollment-therapeutic-clinical-trials-cancer
Only 3-5% of adult cancer patients in US receive treatment within clinical trials About 5% of American adults have ever participated in any clinical trial Oncology: 2-3% of all oncology patients participate Contrast: 50-60% enrollment for pediatric cancer trials (<15 years old) Note: 20% of cancer trials fail due to insufficient enrollment; 11% of research sites enroll zero patients Additional sources: https://www.fightcancer.org/policy-resources/barriers-patient-enrollment-therapeutic-clinical-trials-cancer | https://hints.cancer.gov/docs/Briefs/HINTS_Brief_48.pdf
.28.
ScienceDaily. Global prevalence of chronic disease. ScienceDaily: GBD 2015 Study https://www.sciencedaily.com/releases/2015/06/150608081753.htm (2015)
2.3 billion individuals had more than five ailments (2013) Chronic conditions caused 74% of all deaths worldwide (2019), up from 67% (2010) Approximately 1 in 3 adults suffer from multiple chronic conditions (MCCs) Risk factor exposures: 2B exposed to biomass fuel, 1B to air pollution, 1B smokers Projected economic cost: $47 trillion by 2030 Note: 2.3B with 5+ ailments is more accurate than "2B with chronic disease." One-third of all adults globally have multiple chronic conditions Additional sources: https://www.sciencedaily.com/releases/2015/06/150608081753.htm | https://pmc.ncbi.nlm.nih.gov/articles/PMC10830426/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC6214883/
.29.
C&EN. Annual number of new drugs approved globally: 50. C&EN https://cen.acs.org/pharmaceuticals/50-new-drugs-received-FDA/103/i2 (2025)
50 new drugs approved annually Additional sources: https://cen.acs.org/pharmaceuticals/50-new-drugs-received-FDA/103/i2 | https://www.fda.gov/drugs/development-approval-process-drugs/novel-drug-approvals-fda
.30.
estimates, I. Clinical trial abandonment.
Average: 10% abandoned before completion
.31.
Report, I. Global trial capacity. IQVIA Report: Clinical Trial Subjects Number Drops Due to Decline in COVID-19 Enrollment https://gmdpacademy.org/news/iqvia-report-clinical-trial-subjects-number-drops-due-to-decline-in-covid-19-enrollment/
1.9M participants annually (2022, post-COVID normalization from 4M peak in 2021) Additional sources: https://gmdpacademy.org/news/iqvia-report-clinical-trial-subjects-number-drops-due-to-decline-in-covid-19-enrollment/
.32.
Research & Markets. Global clinical trials market 2024. Research and Markets https://www.globenewswire.com/news-release/2024/04/19/2866012/0/en/Global-Clinical-Trials-Market-Research-Report-2024-An-83-16-Billion-Market-by-2030-AI-Machine-Learning-and-Blockchain-will-Transform-the-Clinical-Trials-Landscape.html (2024)
Global clinical trials market valued at approximately $83 billion in 2024, with projections to reach $83-132 billion by 2030. Additional sources: https://www.globenewswire.com/news-release/2024/04/19/2866012/0/en/Global-Clinical-Trials-Market-Research-Report-2024-An-83-16-Billion-Market-by-2030-AI-Machine-Learning-and-Blockchain-will-Transform-the-Clinical-Trials-Landscape.html | https://www.precedenceresearch.com/clinical-trials-market
.33.
OpenSecrets. Lobbying spend (defense). OpenSecrets https://www.opensecrets.org/federal-lobbying/industries/summary?cycle=2024\&id=D (2024).
34.
GiveWell. Cost per DALY for deworming programs. https://www.givewell.org/international/technical/programs/deworming/cost-effectiveness
Schistosomiasis treatment: $28.19-$70.48 per DALY (using arithmetic means with varying disability weights) Soil-transmitted helminths (STH) treatment: $82.54 per DALY (midpoint estimate) Note: GiveWell explicitly states this 2011 analysis is "out of date" and their current methodology focuses on long-term income effects rather than short-term health DALYs Additional sources: https://www.givewell.org/international/technical/programs/deworming/cost-effectiveness
.35.
Numbers, T. by. Pre-1962 drug development costs and timeline (think by numbers). Think by Numbers: How Many Lives Does FDA Save? https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ (1962)
Historical estimates (1970-1985): USD $226M fully capitalized (2011 prices) 1980s drugs: $65M after-tax R&D (1990 dollars), $194M compounded to approval (1990 dollars) Modern comparison: $2-3B costs, 7-12 years (dramatic increase from pre-1962) Context: 1962 regulatory clampdown reduced new treatment production by 70%, dramatically increasing development timelines and costs Note: Secondary source; less reliable than Congressional testimony Additional sources: https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ | https://en.wikipedia.org/wiki/Cost_of_drug_development | https://www.statnews.com/2018/10/01/changing-1962-law-slash-drug-prices/
.36.
Medicine, N. Drug repurposing rate ( 30%). Nature Medicine https://www.nature.com/articles/s41591-024-03233-x (2024)
Approximately 30% of drugs gain at least one new indication after initial approval. Additional sources: https://www.nature.com/articles/s41591-024-03233-x
.37.
EPI. Education investment economic multiplier (2.1). EPI: Public Investments Outside Core Infrastructure https://www.epi.org/publication/bp348-public-investments-outside-core-infrastructure/
Early childhood education: Benefits 12X outlays by 2050; $8.70 per dollar over lifetime Educational facilities: $1 spent β $1.50 economic returns Energy efficiency comparison: 2-to-1 benefit-to-cost ratio (McKinsey) Private return to schooling: 9% per additional year (World Bank meta-analysis) Note: 2.1 multiplier aligns with benefit-to-cost ratios for educational infrastructure/energy efficiency. Early childhood education shows much higher returns (12X by 2050) Additional sources: https://www.epi.org/publication/bp348-public-investments-outside-core-infrastructure/ | https://documents1.worldbank.org/curated/en/442521523465644318/pdf/WPS8402.pdf | https://freopp.org/whitepapers/establishing-a-practical-return-on-investment-framework-for-education-and-skills-development-to-expand-economic-opportunity/
.38.
PMC. Healthcare investment economic multiplier (1.8). PMC: California Universal Health Care https://pmc.ncbi.nlm.nih.gov/articles/PMC5954824/ (2022)
Healthcare fiscal multiplier: 4.3 (95% CI: 2.5-6.1) during pre-recession period (1995-2007) Overall government spending multiplier: 1.61 (95% CI: 1.37-1.86) Why healthcare has high multipliers: No effect on trade deficits (spending stays domestic); improves productivity & competitiveness; enhances long-run potential output Gender-sensitive fiscal spending (health & care economy) produces substantial positive growth impacts Note: "1.8" appears to be conservative estimate; research shows healthcare multipliers of 4.3 Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC5954824/ | https://cepr.org/voxeu/columns/government-investment-and-fiscal-stimulus | https://ncbi.nlm.nih.gov/pmc/articles/PMC3849102/ | https://set.odi.org/wp-content/uploads/2022/01/Fiscal-multipliers-review.pdf
.39.
Bank, W. Infrastructure investment economic multiplier (1.6). World Bank: Infrastructure Investment as Stimulus https://blogs.worldbank.org/en/ppps/effectiveness-infrastructure-investment-fiscal-stimulus-what-weve-learned (2022)
Infrastructure fiscal multiplier: 1.6 during contractionary phase of economic cycle Average across all economic states: 1.5 (meaning $1 of public investment β $1.50 of economic activity) Time horizon: 0.8 within 1 year, 1.5 within 2-5 years Range of estimates: 1.5-2.0 (following 2008 financial crisis & American Recovery Act) Italian public construction: 1.5-1.9 multiplier US ARRA: 0.4-2.2 range (differential impacts by program type) Economic Policy Institute: Uses 1.6 for infrastructure spending (middle range of estimates) Note: Public investment less likely to crowd out private activity during recessions; particularly effective when monetary policy loose with near-zero rates Additional sources: https://blogs.worldbank.org/en/ppps/effectiveness-infrastructure-investment-fiscal-stimulus-what-weve-learned | https://www.gihub.org/infrastructure-monitor/insights/fiscal-multiplier-effect-of-infrastructure-investment/ | https://cepr.org/voxeu/columns/government-investment-and-fiscal-stimulus | https://www.richmondfed.org/publications/research/economic_brief/2022/eb_22-04
.40.
Mercatus. Military spending economic multiplier (0.6). Mercatus: Defense Spending and Economy https://www.mercatus.org/research/research-papers/defense-spending-and-economy
Ramey (2011): 0.6 short-run multiplier Barro (1981): 0.6 multiplier for WWII spending (war spending crowded out 40Β’ private economic activity per federal dollar) Barro & Redlick (2011): 0.4 within current year, 0.6 over two years; increased govt spending reduces private-sector GDP portions General finding: $1 increase in deficit-financed federal military spending = less than $1 increase in GDP Variation by context: Central/Eastern European NATO: 0.6 on impact, 1.5-1.6 in years 2-3, gradual fall to zero Ramey & Zubairy (2018): Cumulative 1% GDP increase in military expenditure raises GDP by 0.7% Additional sources: https://www.mercatus.org/research/research-papers/defense-spending-and-economy | https://cepr.org/voxeu/columns/world-war-ii-america-spending-deficits-multipliers-and-sacrifice | https://www.rand.org/content/dam/rand/pubs/research_reports/RRA700/RRA739-2/RAND_RRA739-2.pdf
.41.
(BIO), B. I. O. BIO clinical development success rates 2011-2020. Biotechnology Innovation Organization (BIO) https://go.bio.org/rs/490-EHZ-999/images/ClinicalDevelopmentSuccessRates2011_2020.pdf (2021)
Phase I duration: 2.3 years average Total time to market (Phase I-III + approval): 10.5 years average Phase transition success rates: Phase IβII: 63.2%, Phase IIβIII: 30.7%, Phase IIIβApproval: 58.1% Overall probability of approval from Phase I: 12% Note: Largest publicly available study of clinical trial success rates. Efficacy lag = 10.5 - 2.3 = 8.2 years post-safety verification. Additional sources: https://go.bio.org/rs/490-EHZ-999/images/ClinicalDevelopmentSuccessRates2011_2020.pdf
.42.
FDA. FDA-approved prescription drug products (20,000+). FDA https://www.fda.gov/media/143704/download
There are over 20,000 prescription drug products approved for marketing. Additional sources: https://www.fda.gov/media/143704/download
.43.
FDA. FDA GRAS list count ( 570-700). FDA https://www.fda.gov/food/generally-recognized-safe-gras/gras-notice-inventory
The FDA GRAS (Generally Recognized as Safe) list contains approximately 570β700 substances. Additional sources: https://www.fda.gov/food/generally-recognized-safe-gras/gras-notice-inventory
.44.
Drugs.com. FDA drug approval timeline. Drugs.com: FDA Drug Approval Process https://www.drugs.com/fda-approval-process.html
Full timeline (preclinical to market): 12-15 years average (10-15 years common range) Preclinical phase: 3-7 years Clinical development + NDA review: 9 years NDA review alone: 10 months average (standard); 6 months (priority review) Historical (pre-PDUFA): 21-29 months for NDA review Note: "10 years" is accurate for total development timeline (10-15 year range). Modern FDA review is faster (10 months) thanks to PDUFA, but overall timeline remains 12-15 years Additional sources: https://www.drugs.com/fda-approval-process.html | https://www.fdareview.org/issues/the-drug-development-and-approval-process/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC6113340/
.45.
ACLED. Active combat deaths annually. ACLED: Global Conflict Surged 2024 https://acleddata.com/2024/12/12/data-shows-global-conflict-surged-in-2024-the-washington-post/ (2024)
2024: 233,597 deaths (30% increase from 179,099 in 2023) Deadliest conflicts: Ukraine (67,000), Palestine (35,000) Nearly 200,000 acts of violence (25% higher than 2023, double from 5 years ago) One in six people globally live in conflict-affected areas Additional sources: https://acleddata.com/2024/12/12/data-shows-global-conflict-surged-in-2024-the-washington-post/ | https://acleddata.com/media-citation/data-shows-global-conflict-surged-2024-washington-post | https://acleddata.com/conflict-index/index-january-2024/
.46.
UCDP. State violence deaths annually. UCDP: Uppsala Conflict Data Program https://ucdp.uu.se/
Uppsala Conflict Data Program (UCDP): Tracks one-sided violence (organized actors attacking unarmed civilians) UCDP definition: Conflicts causing at least 25 battle-related deaths in calendar year 2023 total organized violence: 154,000 deaths; Non-state conflicts: 20,900 deaths UCDP collects data on state-based conflicts, non-state conflicts, and one-sided violence Specific "2,700 annually" figure for state violence not found in recent UCDP data; actual figures vary annually Additional sources: https://ucdp.uu.se/ | https://en.wikipedia.org/wiki/Uppsala_Conflict_Data_Program | https://ourworldindata.org/grapher/deaths-in-armed-conflicts-by-region
.47.
Data, O. W. in. Terror attack deaths (8,300 annually). Our World in Data: Terrorism https://ourworldindata.org/terrorism (2024)
2023: 8,352 deaths (22% increase from 2022, highest since 2017) 2023: 3,350 terrorist incidents (22% decrease), but 56% increase in avg deaths per attack Global Terrorism Database (GTD): 200,000+ terrorist attacks recorded (2021 version) Maintained by: National Consortium for Study of Terrorism & Responses to Terrorism (START), U. of Maryland Geographic shift: Epicenter moved from Middle East to Central Sahel (sub-Saharan Africa) - now >50% of all deaths Additional sources: https://ourworldindata.org/terrorism | https://reliefweb.int/report/world/global-terrorism-index-2024 | https://www.start.umd.edu/gtd/ | https://ourworldindata.org/grapher/fatalities-from-terrorism
.48.
Health Metrics, I. for & (IHME), E. IHME global burden of disease 2021 (2.88B DALYs, 1.13B YLD). Institute for Health Metrics and Evaluation (IHME) https://vizhub.healthdata.org/gbd-results/ (2024)
In 2021, global DALYs totaled approximately 2.88 billion, comprising 1.75 billion Years of Life Lost (YLL) and 1.13 billion Years Lived with Disability (YLD). This represents a 13% increase from 2019 (2.55B DALYs), largely attributable to COVID-19 deaths and aging populations. YLD accounts for approximately 39% of total DALYs, reflecting the substantial burden of non-fatal chronic conditions. Additional sources: https://vizhub.healthdata.org/gbd-results/ | https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(24 | https://www.healthdata.org/research-analysis/about-gbd
.49.
War, B. W. C. of. Environmental cost of war ($100B annually). Brown Watson Costs of War: Environmental Cost https://watson.brown.edu/costsofwar/costs/social/environment
War on Terror emissions: 1.2B metric tons GHG (equivalent to 257M cars/year) Military: 5.5% of global GHG emissions (2X aviation + shipping combined) US DoD: Worldβs single largest institutional oil consumer, 47th largest emitter if nation Cleanup costs: $500B+ for military contaminated sites Gaza war environmental damage: $56.4B; landmine clearance: $34.6B expected Climate finance gap: Rich nations spend 30X more on military than climate finance Note: Military activities cause massive environmental damage through GHG emissions, toxic contamination, and long-term cleanup costs far exceeding current climate finance commitments Additional sources: https://watson.brown.edu/costsofwar/costs/social/environment | https://earth.org/environmental-costs-of-wars/ | https://transformdefence.org/transformdefence/stats/
.50.
ScienceDaily. Medical research lives saved annually (4.2 million). ScienceDaily: Physical Activity Prevents 4M Deaths https://www.sciencedaily.com/releases/2020/06/200617194510.htm (2020)
Physical activity: 3.9M early deaths averted annually worldwide (15% lower premature deaths than without) COVID vaccines (2020-2024): 2.533M deaths averted, 14.8M life-years preserved; first year alone: 14.4M deaths prevented Cardiovascular prevention: 3 interventions could delay 94.3M deaths over 25 years (antihypertensives alone: 39.4M) Pandemic research response: Millions of deaths averted through rapid vaccine/drug development Additional sources: https://www.sciencedaily.com/releases/2020/06/200617194510.htm | https://pmc.ncbi.nlm.nih.gov/articles/PMC9537923/ | https://www.ahajournals.org/doi/10.1161/CIRCULATIONAHA.118.038160 | https://pmc.ncbi.nlm.nih.gov/articles/PMC9464102/
.51.
SIPRI. 36:1 disparity ratio of spending on weapons over cures. SIPRI: Military Spending https://www.sipri.org/commentary/blog/2016/opportunity-cost-world-military-spending (2016)
Global military spending: $2.7 trillion (2024, SIPRI) Global government medical research: $68 billion (2024) Actual ratio: 39.7:1 in favor of weapons over medical research Military R&D alone: $85B (2004 data, 10% of global R&D) Military spending increases crowd out health: 1% β military = 0.62% β health spending Note: Ratio actually worse than 36:1. Each 1% increase in military spending reduces health spending by 0.62%, with effect more intense in poorer countries (0.962% reduction) Additional sources: https://www.sipri.org/commentary/blog/2016/opportunity-cost-world-military-spending | https://pmc.ncbi.nlm.nih.gov/articles/PMC9174441/ | https://www.congress.gov/crs-product/R45403
.52.
Numbers, T. by. Lost human capital due to war ($270B annually). Think by Numbers: War Costs $74 <https://thinkbynumbers.org/military/war/the-economic-case-for-peace-a-comprehensive-financial-analysis/> (2021)
Lost human capital from war: $300B annually (economic impact of losing skilled/productive individuals to conflict) Broader conflict/violence cost: $14T/year globally 1.4M violent deaths/year; conflict holds back economic development, causes instability, widens inequality, erodes human capital 2002: 48.4M DALYs lost from 1.6M violence deaths = $151B economic value (2000 USD) Economic toll includes: commodity prices, inflation, supply chain disruption, declining output, lost human capital Additional sources: <https://thinkbynumbers.org/military/war/the-economic-case-for-peace-a-comprehensive-financial-analysis/> | https://www.weforum.org/stories/2021/02/war-violence-costs-each-human-5-a-day/ | https://pubmed.ncbi.nlm.nih.gov/19115548/
.53.
PubMed. Psychological impact of war cost ($100B annually). PubMed: Economic Burden of PTSD https://pubmed.ncbi.nlm.nih.gov/35485933/
PTSD economic burden (2018 U.S.): $232.2B total ($189.5B civilian, $42.7B military) Civilian costs driven by: Direct healthcare ($66B), unemployment ($42.7B) Military costs driven by: Disability ($17.8B), direct healthcare ($10.1B) Exceeds costs of other mental health conditions (anxiety, depression) War-exposed populations: 2-3X higher rates of anxiety, depression, PTSD; women and children most vulnerable Note: Actual burden $232B, significantly higher than "$100B" claimed Additional sources: https://pubmed.ncbi.nlm.nih.gov/35485933/ | https://news.va.gov/103611/study-national-economic-burden-of-ptsd-staggering/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC9957523/
.54.
CGDev. UNHCR average refugee support cost. CGDev https://www.cgdev.org/blog/costs-hosting-refugees-oecd-countries-and-why-uk-outlier (2024)
The average cost of supporting a refugee is $1,384 per year. This represents total host country costs (housing, healthcare, education, security). OECD countries average $6,100 per refugee (mean 2022-2023), with developing countries spending $700-1,000. Global weighted average of $1,384 is reasonable given that 75-85% of refugees are in low/middle-income countries. Additional sources: https://www.cgdev.org/blog/costs-hosting-refugees-oecd-countries-and-why-uk-outlier | https://www.unhcr.org/sites/default/files/2024-11/UNHCR-WB-global-cost-of-refugee-inclusion-in-host-country-health-systems.pdf
.55.
Bank, W. World bank trade disruption cost from conflict. World Bank https://www.worldbank.org/en/topic/trade/publication/trading-away-from-conflict
Estimated $616B annual cost from conflict-related trade disruption. World Bank research shows civil war costs an average developing country 30 years of GDP growth, with 20 years needed for trade to return to pre-war levels. Trade disputes analysis shows tariff escalation could reduce global exports by up to $674 billion. Additional sources: https://www.worldbank.org/en/topic/trade/publication/trading-away-from-conflict | https://www.nber.org/papers/w11565 | http://blogs.worldbank.org/en/trade/impacts-global-trade-and-income-current-trade-disputes
.56.
VA. Veteran healthcare cost projections. VA https://department.va.gov/wp-content/uploads/2025/06/2026-Budget-in-Brief.pdf (2026)
VA budget: $441.3B requested for FY 2026 (10% increase). Disability compensation: $165.6B in FY 2024 for 6.7M veterans. PACT Act projected to increase spending by $300B between 2022-2031. Costs under Toxic Exposures Fund: $20B (2024), $30.4B (2025), $52.6B (2026). Additional sources: https://department.va.gov/wp-content/uploads/2025/06/2026-Budget-in-Brief.pdf | https://www.cbo.gov/publication/45615 | https://www.legion.org/information-center/news/veterans-healthcare/2025/june/va-budget-tops-400-billion-for-2025-from-higher-spending-on-mandated-benefits-medical-care
.57.
IQVIA Institute for Human Data Science. The global use of medicines 2024: Outlook to 2028. IQVIA Institute Report https://www.iqvia.com/insights/the-iqvia-institute/reports-and-publications/reports/the-global-use-of-medicines-2024-outlook-to-2028 (2024)
Global days of therapy reached 1.8 trillion in 2019 (234 defined daily doses per person). Diabetes, respiratory, CVD, and cancer account for 71 percent of medicine use. Projected to reach 3.8 trillion DDDs by 2028.
58.
size, D. from global market & ratios, public/private funding. Private industry clinical trial spending.
Private pharmaceutical and biotech industry spends approximately $75-90 billion annually on clinical trials, representing roughly 90% of global clinical trial spending.
59.
IHME Global Burden of Disease (2.55B DALYs), C. from & GDP per capita valuation, global. $109 trillion annual global disease burden.
The global economic burden of disease, including direct healthcare costs (\(8.2 trillion) and lost productivity (\)100.9 trillion from 2.55 billion DALYs Γ \(39,570 per DALY), totals approximately\)109.1 trillion annually.
60.
Trials, A. C. Global government spending on interventional clinical trials: $3-6 billion/year. Applied Clinical Trials https://www.appliedclinicaltrialsonline.com/view/sizing-clinical-research-market
Estimated range based on NIH ( $0.8-5.6B), NIHR ($1.6B total budget), and EU funding ( $1.3B/year). Roughly 5-10% of global market. Additional sources: https://www.appliedclinicaltrialsonline.com/view/sizing-clinical-research-market | https://www.thelancet.com/journals/langlo/article/PIIS2214-109X(20
.61.
Suisse/UBS, C. Credit suisse global wealth report 2023. Credit Suisse/UBS https://www.ubs.com/global/en/family-office-uhnw/reports/global-wealth-report-2023.html (2023)
Total global household wealth: USD 454.4 trillion (2022) Wealth declined by USD 11.3 trillion (-2.4%) in 2022, first decline since 2008 Wealth per adult: USD 84,718 Additional sources: https://www.ubs.com/global/en/family-office-uhnw/reports/global-wealth-report-2023.html
.62.
budgets:, S. component country. Global government medical research spending ($67.5B, 2023β2024). See component country budgets: NIH Budget #nih-budget-fy2025.
63.
SIPRI. Global military spending ($2.72T, 2024). SIPRI https://www.sipri.org/publications/2025/sipri-fact-sheets/trends-world-military-expenditure-2024 (2025).
64.
budgets, E. from major foundation & activities. Nonprofit clinical trial funding estimate.
Nonprofit foundations spend an estimated $2-5 billion annually on clinical trials globally, representing approximately 2-5% of total clinical trial spending.
65.
IQVIA, I. reports: Global pharmaceutical r&d spending.
Total global pharmaceutical R&D spending is approximately $300 billion annually. Clinical trials represent 15-20% of this total ($45-60B), with the remainder going to drug discovery, preclinical research, regulatory affairs, and manufacturing development.
66.
UN. Global population reaches 8 billion. UN: World Population 8 Billion Nov 15 2022 https://www.un.org/en/desa/world-population-reach-8-billion-15-november-2022 (2022)
Milestone: November 15, 2022 (UN World Population Prospects 2022) Day of Eight Billion" designated by UN Added 1 billion people in just 11 years (2011-2022) Growth rate: Slowest since 1950; fell under 1% in 2020 Future: 15 years to reach 9B (2037); projected peak 10.4B in 2080s Projections: 8.5B (2030), 9.7B (2050), 10.4B (2080-2100 plateau) Note: Milestone reached Nov 2022. Population growth slowing; will take longer to add next billion (15 years vs 11 years) Additional sources: https://www.un.org/en/desa/world-population-reach-8-billion-15-november-2022 | https://www.un.org/en/dayof8billion | https://en.wikipedia.org/wiki/Day_of_Eight_Billion
.67.
School, H. K. 3.5% participation tipping point. Harvard Kennedy School https://www.hks.harvard.edu/centers/carr/publications/35-rule-how-small-minority-can-change-world (2020)
The research found that nonviolent campaigns were twice as likely to succeed as violent ones, and once 3.5% of the population were involved, they were always successful. Chenoweth and Maria Stephan studied the success rates of civil resistance efforts from 1900 to 2006, finding that nonviolent movements attracted, on average, four times as many participants as violent movements and were more likely to succeed. Key finding: Every campaign that mobilized at least 3.5% of the population in sustained protest was successful (in their 1900-2006 dataset) Note: The 3.5% figure is a descriptive statistic from historical analysis, not a guaranteed threshold. One exception (Bahrain 2011-2014 with 6%+ participation) has been identified. The rule applies to regime change, not policy change in democracies. Additional sources: https://www.hks.harvard.edu/centers/carr/publications/35-rule-how-small-minority-can-change-world | https://www.hks.harvard.edu/sites/default/files/2024-05/Erica%20Chenoweth_2020-005.pdf | https://www.bbc.com/future/article/20190513-it-only-takes-35-of-people-to-change-the-world | https://en.wikipedia.org/wiki/3.5%25_rule
.68.
NHGRI. Human genome project and CRISPR discovery. NHGRI https://www.genome.gov/11006929/2003-release-international-consortium-completes-hgp (2003)
Your DNA is 3 billion base pairs Read the entire code (Human Genome Project, completed 2003) Learned to edit it (CRISPR, discovered 2012) Additional sources: https://www.genome.gov/11006929/2003-release-international-consortium-completes-hgp | https://www.nobelprize.org/prizes/chemistry/2020/press-release/
.69.
PMC. Only 12% of human interactome targeted. PMC https://pmc.ncbi.nlm.nih.gov/articles/PMC10749231/ (2023)
Mapping 350,000+ clinical trials showed that only 12% of the human interactome has ever been targeted by drugs. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC10749231/
.70.
WHO. ICD-10 code count ( 14,000). WHO https://icd.who.int/browse10/2019/en (2019)
The ICD-10 classification contains approximately 14,000 codes for diseases, signs and symptoms. Additional sources: https://icd.who.int/browse10/2019/en
.71.
Wikipedia. Longevity escape velocity (LEV) - maximum human life extension potential. Wikipedia: Longevity Escape Velocity https://en.wikipedia.org/wiki/Longevity_escape_velocity
Longevity escape velocity: Hypothetical point where medical advances extend life expectancy faster than time passes Term coined by Aubrey de Grey (biogerontologist) in 2004 paper; concept from David Gobel (Methuselah Foundation) Current progress: Science adds 3 months to lifespan per year; LEV requires adding >1 year per year Sinclair (Harvard): "There is no biological upper limit to age" - first person to live to 150 may already be born De Grey: 50% chance of reaching LEV by mid-to-late 2030s; SENS approach = damage repair rather than slowing damage Kurzweil (2024): LEV by 2029-2035, AI will simulate biological processes to accelerate solutions George Church: LEV "in a decade or two" via age-reversal clinical trials Natural lifespan cap: 120-150 years (Jeanne Calment record: 122); engineering approach could bypass via damage repair Key mechanisms: Epigenetic reprogramming, senolytic drugs, stem cell therapy, gene therapy, AI-driven drug discovery Current record: Jeanne Calment (122 years, 164 days) - record unbroken since 1997 Note: LEV is theoretical but increasingly plausible given demonstrated age reversal in mice (109% lifespan extension) and human cells (30-year epigenetic age reversal) Additional sources: https://en.wikipedia.org/wiki/Longevity_escape_velocity | https://pmc.ncbi.nlm.nih.gov/articles/PMC423155/ | https://www.popularmechanics.com/science/a36712084/can-science-cure-death-longevity/ | https://www.diamandis.com/blog/longevity-escape-velocity
.72.
OpenSecrets. Lobbyist statistics for washington d.c. OpenSecrets: Lobbying in US https://en.wikipedia.org/wiki/Lobbying_in_the_United_States
Registered lobbyists: Over 12,000 (some estimates); 12,281 registered (2013) Former government employees as lobbyists: 2,200+ former federal employees (1998-2004), including 273 former White House staffers, 250 former Congress members & agency heads Congressional revolving door: 43% (86 of 198) lawmakers who left 1998-2004 became lobbyists; currently 59% leaving to private sector work for lobbying/consulting firms/trade groups Executive branch: 8% were registered lobbyists at some point before/after government service Additional sources: https://en.wikipedia.org/wiki/Lobbying_in_the_United_States | https://www.opensecrets.org/revolving-door | https://www.citizen.org/article/revolving-congress/ | https://www.propublica.org/article/we-found-a-staggering-281-lobbyists-whove-worked-in-the-trump-administration
.73.
Vaccines, M. Measles vaccination ROI. MDPI Vaccines https://www.mdpi.com/2076-393X/12/11/1210 (2024)
Single measles vaccination: 167:1 benefit-cost ratio. MMR (measles-mumps-rubella) vaccination: 14:1 ROI. Historical US elimination efforts (1966-1974): benefit-cost ratio of 10.3:1 with net benefits exceeding USD 1.1 billion (1972 dollars, or USD 8.0 billion in 2023 dollars). 2-dose MMR programs show direct benefit/cost ratio of 14.2 with net savings of $5.3 billion, and 26.0 from societal perspectives with net savings of $11.6 billion. Additional sources: https://www.mdpi.com/2076-393X/12/11/1210 | https://www.tandfonline.com/doi/full/10.1080/14760584.2024.2367451
.74.
Organization, W. H. Mental health global burden. World Health Organization https://www.who.int/news/item/28-09-2001-the-world-health-report-2001-mental-disorders-affect-one-in-four-people (2022)
One in four people in the world will be affected by mental or neurological disorders at some point in their lives, representing [approximately] 30% of the global burden of disease. Additional sources: https://www.who.int/news/item/28-09-2001-the-world-health-report-2001-mental-disorders-affect-one-in-four-people
.75.
Institute, S. I. P. R. Trends in world military expenditure, 2023. (2024).
76.
Orphanet Journal of Rare Diseases (2024), C. from. Diseases getting first effective treatment each year. Calculated from Orphanet Journal of Rare Diseases (2024) https://ojrd.biomedcentral.com/articles/10.1186/s13023-024-03398-1 (2024)
Under the current system, approximately 10-15 diseases per year receive their FIRST effective treatment. Calculation: 5% of 7,000 rare diseases ( 350) have FDA-approved treatment, accumulated over 40 years of the Orphan Drug Act = 9 rare diseases/year. Adding 5-10 non-rare diseases that get first treatments yields 10-20 total. FDA approves 50 drugs/year, but many are for diseases that already have treatments (me-too drugs, second-line therapies). Only 15 represent truly FIRST treatments for previously untreatable conditions.
77.
NIH. NIH budget (FY 2025). NIH https://www.nih.gov/about-nih/organization/budget (2024)
The budget total of \(47.7 billion also includes\)1.412 billion derived from PHS Evaluation financing... Additional sources: https://www.nih.gov/about-nih/organization/budget | https://officeofbudget.od.nih.gov/
.78.
al., B. et. NIH spending on clinical trials: 3.3%. Bentley et al. https://www.fiercebiotech.com/biotech/nih-spending-clinical-trials-reached-81b-over-decade (2023)
NIH spent $8.1 billion on clinical trials for approved drugs (2010-2019), representing 3.3% of relevant NIH spending. Additional sources: https://www.fiercebiotech.com/biotech/nih-spending-clinical-trials-reached-81b-over-decade | https://www.fiercebiotech.com/biotech/nih-spending-clinical-trials-reached-81b-over-decade
.79.
PMC. Standard medical research ROI ($20k-$100k/QALY). PMC: Cost-effectiveness Thresholds Used by Study Authors https://pmc.ncbi.nlm.nih.gov/articles/PMC10114019/ (1990)
Typical cost-effectiveness thresholds for medical interventions in rich countries range from $50,000 to $150,000 per QALY. The Institute for Clinical and Economic Review (ICER) uses a $100,000-$150,000/QALY threshold for value-based pricing. Between 1990-2021, authors increasingly cited $100,000 (47% by 2020-21) or $150,000 (24% by 2020-21) per QALY as benchmarks for cost-effectiveness. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC10114019/ | https://icer.org/our-approach/methods-process/cost-effectiveness-the-qaly-and-the-evlyg/
.80.
Institute, M. RECOVERY trial 82Γ cost reduction. Manhattan Institute: Slow Costly Trials https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs
RECOVERY trial: $500 per patient ($20M for 48,000 patients = $417/patient) Typical clinical trial: $41,000 median per-patient cost Cost reduction: 80-82Γ cheaper ($41,000 Γ· $500 β 82Γ) Efficiency: $50 per patient per answer (10 therapeutics tested, 4 effective) Dexamethasone estimated to save >630,000 lives Additional sources: https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs | https://pmc.ncbi.nlm.nih.gov/articles/PMC9293394/
.81.
Trials. Patient willingness to participate in clinical trials. Trials: Patientsβ Willingness Survey https://trialsjournal.biomedcentral.com/articles/10.1186/s13063-015-1105-3
Recent surveys: 49-51% willingness (2020-2022) - dramatic drop from 85% (2019) during COVID-19 pandemic Cancer patients when approached: 88% consented to trials (Royal Marsden Hospital) Study type variation: 44.8% willing for drug trial, 76.2% for diagnostic study Top motivation: "Learning more about my health/medical condition" (67.4%) Top barrier: "Worry about experiencing side effects" (52.6%) Additional sources: https://trialsjournal.biomedcentral.com/articles/10.1186/s13063-015-1105-3 | https://www.appliedclinicaltrialsonline.com/view/industry-forced-to-rethink-patient-participation-in-trials | https://pmc.ncbi.nlm.nih.gov/articles/PMC7183682/
.82.
CSDD, T. Cost of drug development.
Various estimates suggest $1.0 - $2.5 billion to bring a new drug from discovery through FDA approval, spread across 10 years. Tufts Center for the Study of Drug Development often cited for $1.0 - $2.6 billion/drug. Industry reports (IQVIA, Deloitte) also highlight $2+ billion figures.
83.
Health, V. in. Average lifetime revenue per successful drug. Value in Health: Sales Revenues for New Therapeutic Agents02754-2/fulltext) https://www.valueinhealthjournal.com/article/S1098-3015(24
Study of 361 FDA-approved drugs from 1995-2014 (median follow-up 13.2 years): Mean lifetime revenue: $15.2 billion per drug Median lifetime revenue: $6.7 billion per drug Revenue after 5 years: $3.2 billion (mean) Revenue after 10 years: $9.5 billion (mean) Revenue after 15 years: $19.2 billion (mean) Distribution highly skewed: top 25 drugs (7%) accounted for 38% of total revenue ($2.1T of $5.5T) Additional sources: https://www.valueinhealthjournal.com/article/S1098-3015(24 | https://www.sciencedirect.com/science/article/pii/S1098301524027542
.84.
Lichtenberg, F. R. How many life-years have new drugs saved? A three-way fixed-effects analysis of 66 diseases in 27 countries, 2000-2013. International Health 11, 403β416 (2019)
Using 3-way fixed-effects methodology (disease-country-year) across 66 diseases in 22 countries, this study estimates that drugs launched after 1981 saved 148.7 million life-years in 2013 alone. The regression coefficients for drug launches 0-11 years prior (beta=-0.031, SE=0.008) and 12+ years prior (beta=-0.057, SE=0.013) on years of life lost are highly significant (p<0.0001). Confidence interval for life-years saved: 79.4M-239.8M (95 percent CI) based on propagated standard errors from Table 2.
85.
Deloitte. Pharmaceutical r&d return on investment (ROI). Deloitte: Measuring Pharmaceutical Innovation 2025 https://www.deloitte.com/ch/en/Industries/life-sciences-health-care/research/measuring-return-from-pharmaceutical-innovation.html (2025)
Deloitteβs annual study of top 20 pharma companies by R&D spend (2010-2024): 2024 ROI: 5.9% (second year of growth after decade of decline) 2023 ROI: 4.3% (estimated from trend) 2022 ROI: 1.2% (historic low since study began, 13-year low) 2021 ROI: 6.8% (record high, inflated by COVID-19 vaccines/treatments) Long-term trend: Declining for over a decade before 2023 recovery Average R&D cost per asset: $2.3B (2022), $2.23B (2024) These returns (1.2-5.9% range) fall far below typical corporate ROI targets (15-20%) Additional sources: https://www.deloitte.com/ch/en/Industries/life-sciences-health-care/research/measuring-return-from-pharmaceutical-innovation.html | https://www.prnewswire.com/news-releases/deloittes-13th-annual-pharmaceutical-innovation-report-pharma-rd-return-on-investment-falls-in-post-pandemic-market-301738807.html | https://hitconsultant.net/2023/02/16/pharma-rd-roi-falls-to-lowest-level-in-13-years/
.86.
Discovery, N. R. D. Drug trial success rate from phase i to approval. Nature Reviews Drug Discovery: Clinical Success Rates https://www.nature.com/articles/nrd.2016.136 (2016)
Overall Phase I to approval: 10-12.8% (conventional wisdom 10%, studies show 12.8%) Recent decline: Average LOA now 6.7% for Phase I (2014-2023 data) Leading pharma companies: 14.3% average LOA (range 8-23%) Varies by therapeutic area: Oncology 3.4%, CNS/cardiovascular lowest at Phase III Phase-specific success: Phase I 47-54%, Phase II 28-34%, Phase III 55-70% Note: 12% figure accurate for historical average. Recent data shows decline to 6.7%, with Phase II as primary attrition point (28% success) Additional sources: https://www.nature.com/articles/nrd.2016.136 | https://pmc.ncbi.nlm.nih.gov/articles/PMC6409418/ | https://academic.oup.com/biostatistics/article/20/2/273/4817524
.87.
SofproMed. Phase 3 cost per trial range. SofproMed https://www.sofpromed.com/how-much-does-a-clinical-trial-cost
Phase 3 clinical trials cost between $20 million and $282 million per trial, with significant variation by therapeutic area and trial complexity. Additional sources: https://www.sofpromed.com/how-much-does-a-clinical-trial-cost | https://www.cbo.gov/publication/57126
.88.
PMC. Pragmatic trial cost per patient (median $97). PMC: Costs of Pragmatic Clinical Trials https://pmc.ncbi.nlm.nih.gov/articles/PMC6508852/
The median cost per participant was $97 (IQR $19β$478), based on 2015 dollars. Systematic review of 64 embedded pragmatic clinical trials. 25% of trials cost <$19/patient; 10 trials exceeded $1,000/patient. U.S. studies median $187 vs non-U.S. median $27. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC6508852/
.89.
WHO. Polio vaccination ROI. WHO https://www.who.int/news-room/feature-stories/detail/sustaining-polio-investments-offers-a-high-return (2019)
For every dollar spent, the return on investment is nearly US$ 39." Total investment cost of US$ 7.5 billion generates projected economic and social benefits of US$ 289.2 billion from sustaining polio assets and integrating them into expanded immunization, surveillance and emergency response programmes across 8 priority countries (Afghanistan, Iraq, Libya, Pakistan, Somalia, Sudan, Syria, Yemen). Additional sources: https://www.who.int/news-room/feature-stories/detail/sustaining-polio-investments-offers-a-high-return
.90.
Olson, M. Big bills left on the sidewalk: Why some nations are rich, and others poor. Journal of Economic Perspectives 10, 3β24 (1996)
Differences between rich and poor countries are primarily due to institutions and policies, not factors of production.
91.
Hayek, F. A. The use of knowledge in society. American Economic Review 35, 519β530 (1945)
The knowledge of the circumstances which we must make use of never exists in concentrated or integrated form but solely as dispersed bits of incomplete and frequently contradictory knowledge which all the separate individuals possess.
92.
Kydland, F. E. & Prescott, E. C. Rules rather than discretion: The inconsistency of optimal plans. Journal of Political Economy 85, 473β492 (1977)
Time-inconsistency describes situations where, with the passing of time, policies that were determined to be optimal yesterday are no longer perceived to be optimal today and are not implemented... This insight shifted the focus of policy analysis from the study of individual policy decisions to the design of institutions that mitigate the time consistency problem.
93.
ICRC. International campaign to ban landmines (ICBL) - ottawa treaty (1997). ICRC https://www.icrc.org/en/doc/resources/documents/article/other/57jpjn.htm (1997)
ICBL: Founded 1992 by 6 NGOs (Handicap International, Human Rights Watch, Medico International, Mines Advisory Group, Physicians for Human Rights, Vietnam Veterans of America Foundation) Started with ONE staff member: Jody Williams as founding coordinator Grew to 1,000+ organizations in 60 countries by 1997 Ottawa Process: 14 months (October 1996 - December 1997) Convention signed by 122 states on December 3, 1997; entered into force March 1, 1999 Achievement: Nobel Peace Prize 1997 (shared by ICBL and Jody Williams) Government funding context: Canada established $100M CAD Canadian Landmine Fund over 10 years (1997); International donors provided $169M in 1997 for mine action (up from $100M in 1996) Additional sources: https://www.icrc.org/en/doc/resources/documents/article/other/57jpjn.htm | https://en.wikipedia.org/wiki/International_Campaign_to_Ban_Landmines | https://www.nobelprize.org/prizes/peace/1997/summary/ | https://un.org/press/en/1999/19990520.MINES.BRF.html | https://www.the-monitor.org/en-gb/reports/2003/landmine-monitor-2003/mine-action-funding.aspx
.94.
OpenSecrets. Revolving door: Former members of congress. (2024)
388 former members of Congress are registered as lobbyists. Nearly 5,400 former congressional staffers have left Capitol Hill to become federal lobbyists in the past 10 years. Additional sources: https://www.opensecrets.org/revolving-door
.95.
Kinch, M. S. & Griesenauer, R. H. Lost medicines: A longer view of the pharmaceutical industry with the potential to reinvigorate discovery. Drug Discovery Today 24, 875β880 (2019)
Research identified 1,600+ medicines available in 1962. The 1950s represented industry high-water mark with >30 new products in five of ten years; this rate would not be replicated until late 1990s. More than half (880) of these medicines were lost following implementation of Kefauver-Harris Amendment. The peak of 1962 would not be seen again until early 21st century. By 2016 number of organizations actively involved in R&D at level not seen since 1914.
96.
Wikipedia. US military spending reduction after WWII. Wikipedia https://en.wikipedia.org/wiki/Demobilization_of_United_States_Armed_Forces_after_World_War_II (2020)
Peaking at over $81 billion in 1945, the U.S. military budget plummeted to approximately $13 billion by 1948, representing an 84% decrease. The number of personnel was reduced almost 90%, from more than 12 million to about 1.5 million between mid-1945 and mid-1947. Defense spending exceeded 41 percent of GDP in 1945. After World War II, the US reduced military spending to 7.2 percent of GDP by 1948. Defense spending doubled from the 1948 low to 15 percent at the height of the Korean War in 1953. Additional sources: https://en.wikipedia.org/wiki/Demobilization_of_United_States_Armed_Forces_after_World_War_II | https://www.americanprogress.org/article/a-historical-perspective-on-military-budgets/ | https://www.stlouisfed.org/on-the-economy/2020/february/war-highest-military-spending-measured | https://www.usgovernmentspending.com/defense_spending_history
.97.
Baily, M. N. Pre-1962 drug development costs (baily 1972). Baily (1972) https://samizdathealth.org/wp-content/uploads/2020/12/hlthaff.1.2.6.pdf (1972)
Pre-1962: Average cost per new chemical entity (NCE) was $6.5 million (1980 dollars) Inflation-adjusted to 2024 dollars: $6.5M (1980) β $22.5M (2024), using CPI multiplier of 3.46Γ Real cost increase (inflation-adjusted): $22.5M (pre-1962) β $2,600M (2024) = 116Γ increase Note: This represents the most comprehensive academic estimate of pre-1962 drug development costs based on empirical industry data Additional sources: https://samizdathealth.org/wp-content/uploads/2020/12/hlthaff.1.2.6.pdf
.98.
Numbers, T. by. Pre-1962 physician-led clinical trials. Think by Numbers: How Many Lives Does FDA Save? https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ (1966)
Pre-1962: Physicians could report real-world evidence directly 1962 Drug Amendments replaced "premarket notification" with "premarket approval", requiring extensive efficacy testing Impact: New regulatory clampdown reduced new treatment production by 70%; lifespan growth declined from 4 years/decade to 2 years/decade Drug Efficacy Study Implementation (DESI): NAS/NRC evaluated 3,400+ drugs approved 1938-1962 for safety only; reviewed >3,000 products, >16,000 therapeutic claims FDA has had authority to accept real-world evidence since 1962, clarified by 21st Century Cures Act (2016) Note: Specific "144,000 physicians" figure not verified in sources Additional sources: https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ | https://www.fda.gov/drugs/enforcement-activities-fda/drug-efficacy-study-implementation-desi | http://www.nasonline.org/about-nas/history/archives/collections/des-1966-1969-1.html
.99.
GAO. 95% of diseases have 0 FDA-approved treatments. GAO https://www.gao.gov/products/gao-25-106774 (2025)
95% of diseases have no treatment Additional sources: https://www.gao.gov/products/gao-25-106774 | https://globalgenes.org/rare-disease-facts/
.100.
Oren Cass, M. I. RECOVERY trial cost per patient. Oren Cass https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs (2023)
The RECOVERY trial, for example, cost only about \(500 per patient... By contrast, the median per-patient cost of a pivotal trial for a new therapeutic is around\)41,000. Additional sources: https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs
.101.
al., N. E. Γ. et. RECOVERY trial global lives saved ( 1 million). NHS England: 1 Million Lives Saved https://www.england.nhs.uk/2021/03/covid-treatment-developed-in-the-nhs-saves-a-million-lives/ (2021)
Dexamethasone saved 1 million lives worldwide (NHS England estimate, March 2021, 9 months after discovery). UK alone: 22,000 lives saved. Methodology: Γguas et al. Nature Communications 2021 estimated 650,000 lives (range: 240,000-1,400,000) for July-December 2020 alone, based on RECOVERY trial mortality reductions (36% for ventilated, 18% for oxygen-only patients) applied to global COVID hospitalizations. June 2020 announcement: Dexamethasone reduced deaths by up to 1/3 (ventilated patients), 1/5 (oxygen patients). Impact immediate: Adopted into standard care globally within hours of announcement. Additional sources: https://www.england.nhs.uk/2021/03/covid-treatment-developed-in-the-nhs-saves-a-million-lives/ | https://www.nature.com/articles/s41467-021-21134-2 | https://pharmaceutical-journal.com/article/news/steroid-has-saved-the-lives-of-one-million-covid-19-patients-worldwide-figures-show | https://www.recoverytrial.net/news/recovery-trial-celebrates-two-year-anniversary-of-life-saving-dexamethasone-result
.102.
Museum, N. S. 11. M. &. September 11 attack facts. (2024)
2,977 people were killed in the September 11, 2001 attacks: 2,753 at the World Trade Center, 184 at the Pentagon, and 40 passengers and crew on United Flight 93 in Shanksville, Pennsylvania.
103.
Bank, W. World bank singapore economic data. World Bank https://data.worldbank.org/country/singapore (2024)
Singapore GDP per capita (2023): $82,000 - among highest in the world Government spending: 15% of GDP (vs US 38%) Life expectancy: 84.1 years (vs US 77.5 years) Singapore demonstrates that low government spending can coexist with excellent outcomes Additional sources: https://data.worldbank.org/country/singapore
.104.
Fund, I. M. IMF singapore government spending data. (2024)
Singapore government spending is approximately 15% of GDP This is 23 percentage points lower than the United States (38%) Despite lower spending, Singapore achieves excellent outcomes: - Life expectancy: 84.1 years (vs US 77.5) - Low crime, world-class infrastructure, AAA credit rating Additional sources: https://www.imf.org/en/Countries/SGP
.105.
Organization, W. H. WHO life expectancy data by country. (2024)
Life expectancy at birth varies significantly among developed nations: Switzerland: 84.0 years (2023) Singapore: 84.1 years (2023) Japan: 84.3 years (2023) United States: 77.5 years (2023) - 6.5 years below Switzerland, Singapore Global average: 73 years Note: US spends more per capita on healthcare than any other nation, yet achieves lower life expectancy Additional sources: https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates/ghe-life-expectancy-and-healthy-life-expectancy
.106.
CSIS. Smallpox eradication ROI. CSIS https://www.csis.org/analysis/smallpox-eradication-model-global-cooperation.
107.
PMC. Contribution of smoking reduction to life expectancy gains. PMC: Benefits Smoking Cessation Longevity https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1447499/ (2012)
Population-level: Up to 14% (9% men, 14% women) of total life expectancy gain since 1960 due to tobacco control efforts Individual cessation benefits: Quitting at age 35 adds 6.9-8.5 years (men), 6.1-7.7 years (women) vs continuing smokers By cessation age: Age 25-34 = 10 years gained; age 35-44 = 9 years; age 45-54 = 6 years; age 65 = 2.0 years (men), 3.7 years (women) Cessation before age 40: Reduces death risk by 90% Long-term cessation: 10+ years yields survival comparable to never smokers, averts 10 years of life lost Recent cessation: <3 years averts 5 years of life lost Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1447499/ | https://www.cdc.gov/pcd/issues/2012/11_0295.htm | https://www.ajpmonline.org/article/S0749-3797(24 | https://www.nejm.org/doi/full/10.1056/NEJMsa1211128
.108.
ICER. Value per QALY (standard economic value). ICER https://icer.org/wp-content/uploads/2024/02/Reference-Case-4.3.25.pdf (2024)
Standard economic value per QALY: $100,000β$150,000. This is the US and global standard willingness-to-pay threshold for interventions that add costs. Dominant interventions (those that save money while improving health) are favorable regardless of this threshold. Additional sources: https://icer.org/wp-content/uploads/2024/02/Reference-Case-4.3.25.pdf
.109.
GAO. Annual cost of u.s. Sugar subsidies. GAO: Sugar Program https://www.gao.gov/products/gao-24-106144
Consumer costs: $2.5-3.5 billion per year (GAO estimate) Net economic cost: $1 billion per year 2022: US consumers paid 2X world price for sugar Program costs $3-4 billion/year but no federal budget impact (costs passed directly to consumers via higher prices) Employment impact: 10,000-20,000 manufacturing jobs lost annually in sugar-reliant industries (confectionery, etc.) Multiple studies confirm: Sweetener Users Association ($2.9-3.5B), AEI ($2.4B consumer cost), Beghin & Elobeid ($2.9-3.5B consumer surplus) Additional sources: https://www.gao.gov/products/gao-24-106144 | https://www.heritage.org/agriculture/report/the-us-sugar-program-bad-consumers-bad-agriculture-and-bad-america | https://www.aei.org/articles/the-u-s-spends-4-billion-a-year-subsidizing-stalinist-style-domestic-sugar-production/
.110.
Bank, W. Swiss military budget as percentage of GDP. World Bank: Military Expenditure https://data.worldbank.org/indicator/MS.MIL.XPND.GD.ZS?locations=CH
2023: 0.70272% of GDP (World Bank) 2024: CHF 5.95 billion official military spending When including militia system costs: 1% GDP (CHF 8.75B) Comparison: Near bottom in Europe; only Ireland, Malta, Moldova spend less (excluding microstates with no armies) Additional sources: https://data.worldbank.org/indicator/MS.MIL.XPND.GD.ZS?locations=CH | https://www.avenir-suisse.ch/en/blog-defence-spending-switzerland-is-in-better-shape-than-it-seems/ | https://tradingeconomics.com/switzerland/military-expenditure-percent-of-gdp-wb-data.html
.111.
Bank, W. Switzerland vs. US GDP per capita comparison. World Bank: Switzerland GDP Per Capita https://data.worldbank.org/indicator/NY.GDP.PCAP.CD?locations=CH
2024 GDP per capita (PPP-adjusted): Switzerland $93,819 vs United States $75,492 Switzerlandβs GDP per capita 24% higher than US when adjusted for purchasing power parity Nominal 2024: Switzerland $103,670 vs US $85,810 Additional sources: https://data.worldbank.org/indicator/NY.GDP.PCAP.CD?locations=CH | https://tradingeconomics.com/switzerland/gdp-per-capita-ppp | https://www.theglobaleconomy.com/USA/gdp_per_capita_ppp/
.112.
Economic Co-operation, O. for & Development. OECD government spending as percentage of GDP. (2024)
OECD government spending data shows significant variation among developed nations: United States: 38.0% of GDP (2023) Switzerland: 35.0% of GDP - 3 percentage points lower than US Singapore: 15.0% of GDP - 23 percentage points lower than US (per IMF data) OECD average: approximately 40% of GDP Additional sources: https://data.oecd.org/gga/general-government-spending.htm
.113.
Economic Co-operation, O. for & Development. OECD median household income comparison. (2024)
Median household disposable income varies significantly across OECD nations: United States: $77,500 (2023) Switzerland: $55,000 PPP-adjusted (lower nominal but comparable purchasing power) Singapore: $75,000 PPP-adjusted Additional sources: https://data.oecd.org/hha/household-disposable-income.htm
.114.
Institute, C. Chance of dying from terrorism statistic. Cato Institute: Terrorism and Immigration Risk Analysis https://www.cato.org/policy-analysis/terrorism-immigration-risk-analysis
Chance of American dying in foreign-born terrorist attack: 1 in 3.6 million per year (1975-2015) Including 9/11 deaths; annual murder rate is 253x higher than terrorism death rate More likely to die from lightning strike than foreign terrorism Note: Comprehensive 41-year study shows terrorism risk is extremely low compared to everyday dangers Additional sources: https://www.cato.org/policy-analysis/terrorism-immigration-risk-analysis | https://www.nbcnews.com/news/us-news/you-re-more-likely-die-choking-be-killed-foreign-terrorists-n715141
.115.
Wikipedia. Thalidomide scandal: Worldwide cases and mortality. Wikipedia https://en.wikipedia.org/wiki/Thalidomide_scandal
The total number of embryos affected by the use of thalidomide during pregnancy is estimated at 10,000, of whom about 40% died around the time of birth. More than 10,000 children in 46 countries were born with deformities such as phocomelia. Additional sources: https://en.wikipedia.org/wiki/Thalidomide_scandal
.116.
One, P. Health and quality of life of thalidomide survivors as they age. PLOS One https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0210222 (2019)
Study of thalidomide survivors documenting ongoing disability impacts, quality of life, and long-term health outcomes. Survivors (now in their 60s) continue to experience significant disability from limb deformities, organ damage, and other effects. Additional sources: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0210222
.117.
Bureau, U. C. Historical world population estimates. US Census Bureau https://www.census.gov/data/tables/time-series/demo/international-programs/historical-est-worldpop.html
US Census Bureau historical estimates of world population by country and region (1950-2050). US population in 1960: 180 million of 3 billion worldwide (6%). Additional sources: https://www.census.gov/data/tables/time-series/demo/international-programs/historical-est-worldpop.html
.118.
NCBI, F. S. via. Trial costs, FDA study. FDA Study via NCBI https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6248200/
Overall, the 138 clinical trials had an estimated median (IQR) cost of \(19.0 million (\)12.2 million-\(33.1 million)... The clinical trials cost a median (IQR) of\)41,117 (\(31,802-\)82,362) per patient. Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6248200/
.119.
GBD 2019 Diseases and Injuries Collaborators. Global burden of disease study 2019: Disability weights. The Lancet 396, 1204β1222 (2020)
Disability weights for 235 health states used in Global Burden of Disease calculations. Weights range from 0 (perfect health) to 1 (death equivalent). Chronic conditions like diabetes (0.05-0.35), COPD (0.04-0.41), depression (0.15-0.66), and cardiovascular disease (0.04-0.57) show substantial variation by severity. Treatment typically reduces disability weights by 50-80 percent for manageable chronic conditions.
120.
EPI. CEO compensation. EPI https://www.epi.org/blog/ceo-pay-increased-in-2024-and-is-now-281-times-that-of-the-typical-worker-new-epi-landing-page-has-all-the-details/ (2024)
S&P 500 average: $18.9M (2024) | $9,087/hour | 285:1 CEO-to-worker ratio Additional sources: https://www.epi.org/blog/ceo-pay-increased-in-2024-and-is-now-281-times-that-of-the-typical-worker-new-epi-landing-page-has-all-the-details/
.121.
WHO. Annual global economic burden of alzheimerβs and other dementias. WHO: Dementia Fact Sheet https://www.who.int/news-room/fact-sheets/detail/dementia (2019)
Global cost: $1.3 trillion (2019 WHO-commissioned study) 50% from informal caregivers (family/friends, 5 hrs/day) 74% of costs in high-income countries despite 61% of patients in LMICs $818B (2010) β $1T (2018) β $1.3T (2019) - rapid growth Note: Costs increased 35% from 2010-2015 alone. Informal care represents massive hidden economic burden Additional sources: https://www.who.int/news-room/fact-sheets/detail/dementia | https://alz-journals.onlinelibrary.wiley.com/doi/10.1002/alz.12901
.122.
Oncology, J. Annual global economic burden of cancer. JAMA Oncology: Global Cost 2020-2050 https://jamanetwork.com/journals/jamaoncology/fullarticle/2801798 (2020)
2020-2050 projection: $25.2 trillion total ($840B/year average) 2010 annual cost: $1.16 trillion (direct costs only) Recent estimate: $3 trillion/year (all costs included) Top 5 cancers: lung (15.4%), colon/rectum (10.9%), breast (7.7%), liver (6.5%), leukemia (6.3%) Note: China/US account for 45% of global burden; 75% of deaths in LMICs but only 50.0% of economic cost Additional sources: https://jamanetwork.com/journals/jamaoncology/fullarticle/2801798 | https://www.nature.com/articles/d41586-023-00634-9
.123.
CDC. U.s. Chronic disease healthcare spending. CDC https://www.cdc.gov/chronic-disease/data-research/facts-stats/index.html
Chronic diseases account for 90% of U.S. healthcare spending ( $3.7T/year). Additional sources: https://www.cdc.gov/chronic-disease/data-research/facts-stats/index.html
.124.
Care, D. Annual global economic burden of diabetes. Diabetes Care: Global Economic Burden https://diabetesjournals.org/care/article/41/5/963/36522/Global-Economic-Burden-of-Diabetes-in-Adults
2015: $1.3 trillion (1.8% of global GDP) 2030 projections: $2.1T-2.5T depending on scenario IDF health expenditure: $760B (2019) β $845B (2045 projected) 2/3 direct medical costs ($857B), 1/3 indirect costs (lost productivity) Note: Costs growing rapidly; expected to exceed $2T by 2030 Additional sources: https://diabetesjournals.org/care/article/41/5/963/36522/Global-Economic-Burden-of-Diabetes-in-Adults | https://www.thelancet.com/journals/landia/article/PIIS2213-8587(17
.125.
World Bank, B. of E. A. US GDP 2024 ($28.78 trillion). World Bank https://data.worldbank.org/indicator/NY.GDP.MKTP.CD?locations=US (2024)
US GDP reached $28.78 trillion in 2024, representing approximately 26% of global GDP. Additional sources: https://data.worldbank.org/indicator/NY.GDP.MKTP.CD?locations=US | https://www.bea.gov/news/2024/gross-domestic-product-fourth-quarter-and-year-2024-advance-estimate
.126.
Cardiology, I. J. of. Annual global economic burden of heart disease. Intβl Journal of Cardiology: Global Heart Failure Burden02238-9/abstract) https://www.internationaljournalofcardiology.com/article/S0167-5273(13 (2050)
Heart failure alone: $108 billion/year (2012 global analysis, 197 countries) US CVD: $555B (2016) β projected $1.8T by 2050 LMICs total CVD loss: $3.7T cumulative (2011-2015, 5-year period) CVD is costliest disease category in most developed nations Note: No single $2.1T global figure found; estimates vary widely by scope and year Additional sources: https://www.internationaljournalofcardiology.com/article/S0167-5273(13 | https://www.ahajournals.org/doi/10.1161/CIR.0000000000001258
.127.
CSV, S. U. L. E. F. B. 1543-2019. US life expectancy growth 1880-1960: 3.82 years per decade. (2019)
Pre-1962: 3.82 years/decade Post-1962: 1.54 years/decade Reduction: 60% decline in life expectancy growth rate Additional sources: https://ourworldindata.org/life-expectancy | https://www.mortality.org/ | https://www.cdc.gov/nchs/nvss/mortality_tables.htm
.128.
CSV, S. U. L. E. F. B. 1543-2019. Post-1962 slowdown in life expectancy gains. (2019)
Pre-1962 (1880-1960): 3.82 years/decade Post-1962 (1962-2019): 1.54 years/decade Reduction: 60% decline Temporal correlation: Slowdown occurred immediately after 1962 Kefauver-Harris Amendment See detailed calculation: [life-expectancy-increase-pre-1962](#life-expectancy-increase-pre-1962) Additional sources: https://ourworldindata.org/life-expectancy | https://www.mortality.org/ | https://www.cdc.gov/nchs/nvss/mortality_tables.htm
.129.
Disease Control, C. for & Prevention. US life expectancy 2023. (2024)
US life expectancy at birth was 77.5 years in 2023 Male life expectancy: 74.8 years Female life expectancy: 80.2 years This is 6-7 years lower than peer developed nations despite higher healthcare spending Additional sources: https://www.cdc.gov/nchs/fastats/life-expectancy.htm
.130.
Bureau, U. C. US median household income 2023. (2024)
US median household income was $77,500 in 2023 Real median household income declined 0.8% from 2022 Gini index: 0.467 (income inequality measure) Additional sources: https://www.census.gov/library/publications/2024/demo/p60-282.html
.131.
Statista. US military budget as percentage of GDP. Statista https://www.statista.com/statistics/262742/countries-with-the-highest-military-spending/ (2024)
U.S. military spending amounted to 3.5% of GDP in 2024. In 2024, the U.S. spent nearly $1 trillion on its military budget, equal to 3.4% of GDP. Additional sources: https://www.statista.com/statistics/262742/countries-with-the-highest-military-spending/ | https://www.sipri.org/sites/default/files/2025-04/2504_fs_milex_2024.pdf
.132.
Bureau, U. C. Number of registered or eligible voters in the u.s. US Census Bureau https://www.census.gov/newsroom/press-releases/2025/2024-presidential-election-voting-registration-tables.html (2024)
73.6% (or 174 million people) of the citizen voting-age population was registered to vote in 2024 (Census Bureau). More than 211 million citizens were active registered voters (86.6% of citizen voting age population) according to the Election Assistance Commission. Additional sources: https://www.census.gov/newsroom/press-releases/2025/2024-presidential-election-voting-registration-tables.html | https://www.eac.gov/news/2025/06/30/us-election-assistance-commission-releases-2024-election-administration-and-voting
.133.
Senate, U. S. Treaties. U.S. Senate https://www.senate.gov/about/powers-procedures/treaties.htm
The Constitution provides that the president βshall have Power, by and with the Advice and Consent of the Senate, to make Treaties, provided two-thirds of the Senators present concurβ (Article II, section 2). Treaties are formal agreements with foreign nations that require two-thirds Senate approval. 67 senators (two-thirds of 100) must vote to ratify a treaty for it to take effect. Additional sources: https://www.senate.gov/about/powers-procedures/treaties.htm
.134.
Commission, F. E. Statistical summary of 24-month campaign activity of the 2023-2024 election cycle. (2023)
Presidential candidates raised $2 billion; House and Senate candidates raised $3.8 billion and spent $3.7 billion; PACs raised $15.7 billion and spent $15.5 billion. Total federal campaign spending approximately $20 billion. Additional sources: https://www.fec.gov/updates/statistical-summary-of-24-month-campaign-activity-of-the-2023-2024-election-cycle/
.135.
OpenSecrets. Federal lobbying hit record $4.4 billion in 2024. (2024)
Total federal lobbying reached record $4.4 billion in 2024. The $150 million increase in lobbying continues an upward trend that began in 2016. Additional sources: https://www.opensecrets.org/news/2025/02/federal-lobbying-set-new-record-in-2024/
.136.
Kirk (2011), H. &. Valley of death in drug development. (2011)
The overall failure rate of drugs that passed into Phase 1 trials to final approval is 90%. This lack of translation from promising preclinical findings to success in human trials is known as the "valley of death." Estimated 30-50% of promising compounds never proceed to Phase 2/3 trials primarily due to funding barriers rather than scientific failure. The late-stage attrition rate for oncology drugs is as high as 70% in Phase II and 59% in Phase III trials.
137.
DOT. DOT value of statistical life ($13.6M). DOT: VSL Guidance 2024 https://www.transportation.gov/office-policy/transportation-policy/revised-departmental-guidance-on-valuation-of-a-statistical-life-in-economic-analysis (2024)
Current VSL (2024): $13.7 million (updated from $13.6M) Used in cost-benefit analyses for transportation regulations and infrastructure Methodology updated in 2013 guidance, adjusted annually for inflation and real income VSL represents aggregate willingness to pay for safety improvements that reduce fatalities by one Note: DOT has published VSL guidance periodically since 1993. Current $13.7M reflects 2024 inflation/income adjustments Additional sources: https://www.transportation.gov/office-policy/transportation-policy/revised-departmental-guidance-on-valuation-of-a-statistical-life-in-economic-analysis | https://www.transportation.gov/regulations/economic-values-used-in-analysis
.138.
ONE, P. Cost per DALY for vitamin a supplementation. PLOS ONE: Cost-effectiveness of "Golden Mustard" for Treating Vitamin A Deficiency in India (2010) https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012046 (2010)
India: $23-$50 per DALY averted (least costly intervention, $1,000-$6,100 per death averted) Sub-Saharan Africa (2022): $220-$860 per DALY (Burkina Faso: $220, Kenya: $550, Nigeria: $860) WHO estimates for Africa: $40 per DALY for fortification, $255 for supplementation Uganda fortification: $18-$82 per DALY (oil: $18, sugar: $82) Note: Wide variation reflects differences in baseline VAD prevalence, coverage levels, and whether intervention is supplementation or fortification Additional sources: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012046 | https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0266495
.139.
News, U. Clean water & sanitation (LMICs) ROI. UN News https://news.un.org/en/story/2014/11/484032 (2014).
140.
PMC. Cost-effectiveness threshold ($50,000/QALY). PMC https://pmc.ncbi.nlm.nih.gov/articles/PMC5193154/
The $50,000/QALY threshold is widely used in US health economics literature, originating from dialysis cost benchmarks in the 1980s. In US cost-utility analyses, 77.5% of authors use either $50,000 or $100,000 per QALY as reference points. Most successful health programs cost $3,000-10,000 per QALY. WHO-CHOICE uses GDP per capita multiples (1Γ GDP/capita = "very cost-effective", 3Γ GDP/capita = "cost-effective"), which for the US ( $70,000 GDP/capita) translates to $70,000-$210,000/QALY thresholds. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC5193154/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC9278384/
.141.
Institute, I. B. Chronic illness workforce productivity loss. Integrated Benefits Institute 2024 https://www.ibiweb.org/resources/chronic-conditions-in-the-us-workforce-prevalence-trends-and-productivity-impacts (2024)
78.4% of U.S. employees have at least one chronic condition (7% increase since 2021) 58% of employees report physical chronic health conditions 28% of all employees experience productivity loss due to chronic conditions Average productivity loss: $4,798 per employee per year Employees with 3+ chronic conditions miss 7.8 days annually vs 2.2 days for those without Note: 28% productivity loss translates to roughly 11 hours per week (28% of 40-hour workweek) Additional sources: https://www.ibiweb.org/resources/chronic-conditions-in-the-us-workforce-prevalence-trends-and-productivity-impacts | https://www.onemedical.com/mediacenter/study-finds-more-than-half-of-employees-are-living-with-chronic-conditions-including-1-in-3-gen-z-and-millennial-employees/ | https://debeaumont.org/news/2025/poll-the-toll-of-chronic-health-conditions-on-employees-and-workplaces/
.142.
Rare Diseases (2024), O. J. of. Rare disease treatment gap. Orphanet Journal of Rare Diseases (2024) https://ojrd.biomedcentral.com/articles/10.1186/s13023-024-03398-1 (2024)
Most patients wait 5 to 10 years to get an accurate diagnosis - and only about 5% of rare diseases have an FDA-approved treatment. Over the 40 years of the ODA, 6,340 orphan drug designations were granted, representing drug development for 1,079 rare diseases out of 7,000-10,000 known rare conditions.
Reuse
Copyright
Β© 2025 Mike P. Sinn